4,67 von 5 Sterne
Loading...
Was man unter Achsensymmetrie versteht ist für dich noch unklar und die Berechnung achselsymmetrischer Funktionen fällt dir noch schwer? Das können wir ganz schnell ändern!
In diesem Artikel zeigen wir dir …
- … was Achsensymmetrie ist
- … welche Figuren achsensymmetrisch sind
- … und wie man diese berechnet
Also lasst uns zuerst klären, was Achsensymmetrie überhaupt ist.
Was ist Achsensymmetrie? – Eine einfache Definition
Wenn man das Wort Achsensymmetrie in die beiden Begriffe “Achse” und “Symmetrie” teilt, kommt man ganz schnell dahinter, was Achsensymmetrie ist.
- Auch bekannt als Symmetrieachse oder Spiegelachse
- Es wird dadurch eine Figur oder Funktion gespiegelt
- beide Hälften sind deckungsgleich
- Wenn man eine Figur z.B. Rechteck in der Hälfte faltet und die beiden Teile genau aufeinander passen, handelt es sich um eine achsensymmetrische Figur
Achsensymmetrie wird auch Spiegelsymmetrie genannt.
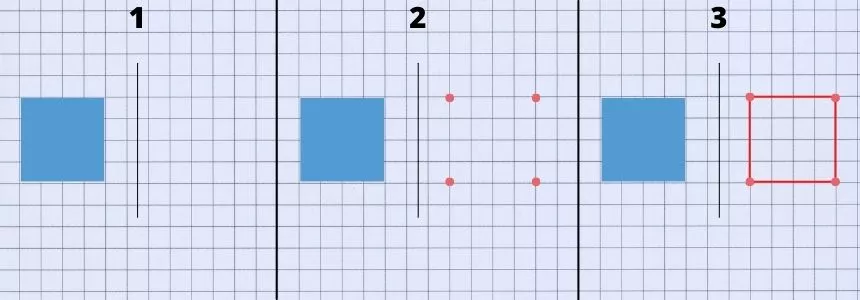
So spiegelst du eine Figur (siehe Abbildung):
- Zeichne eine Symmetrieachse neben die Figur.
- Spiegel alle Eckpunkte der Figur an der Spiegelachse.
- Die gespiegelten Punkte können jetzt miteinander verbunden werden.
Tipp: Wenn du eine Figur spiegelst oder die Symmetrieachsen in eine Figur einzeichnest, mache dieses am besten auf einem karierten Papier.
Die vertikalen und horizontalen Linien dienen dir dabei zur Orientierung und erleichtern dir das Spiegeln der Figur.
Welche Figuren sind achsensymmetrisch?
Die Theorie zu achsensymmetrischen Figuren haben wir nun geklärt. Lasst uns jetzt konkret auf Figuren gucken, die die Eigenschaft der Achsensymmetrie haben.
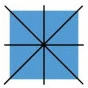
Ein Quadrat hat immer vier Symmetrieachsen. Zwei verlaufen durch die Mitte und zwei durch die Ecken des Quadrates.
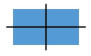
Bei einem Rechteck lassen sich zwei Symmetrieachsen einzeichnen.
Drei Symmetrieachsen sind bei einem gleichseitigen Dreieck zu finden.
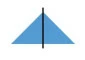
Ein gleichschenkliges Dreieck hat dagegen nur eine Spiegelachse.
Auch ein gleichschenkliges Trapez hat nur eine Spiegelachse.
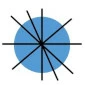
Bei einem Kreis verlaufen die Symmetrieachsen durch den Mittelpunkt. Ein Kreis hat unendlich viele Spiegelachsen.
Auf achsensymmetrische Figuren treffen wir täglich in unserem Alltag. Schau dich einfach mal in deinem Zimmer um und du entdeckst zahlreiche Beispiele für Achsensymmetrie.
Symmetrie zur y-Achse – Was du wissen musst!
- Wie schon erwähnt können auch Funktionen achsensymmetrisch sein.
- Bei Funktionen muss dabei die Symmetrie zur y-Achse nachgewiesen werden. Das bedeutet, dass die Funktion spiegelsymmetrisch zur y-Achse ist und an eben dieser gespiegelt werden kann.
- Jeder Punkt auf der Kurve der Funktion bildet bei der Spiegelung ebenfalls ein Kurvenpunkt ab.
Wenn f(x) = f(-x) gilt, ist eine Funktion achsensymmetrisch zur y-Achse.
So ermittelst du zur y-Achse symmetrische Funktionen:
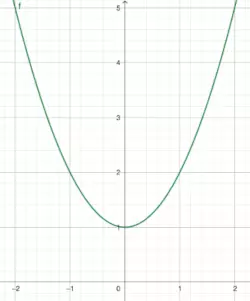
Ist f(x) = x2 + 1 achsensymmetrisch?
Nochmal zur Wiederholung: Wenn f(x) = f(-x) gilt, ist die Funktion achsensymmetrisch.
- Der erste Schritt ist es nun f(-x) zu berechnen. Dazu musst du einfach ein -x anstelle des x in der Funktion schreiben. In unserer Funktion sieht das dann so aus: f(-x) = (-x)2 + 1 = (-x) * (-x) +1 = x2 + 1
- Im nächsten Schritt vergleichst du die beiden Funktionen f(-x) und f(x): f(-x) = x2 + 1 = f(x)
- Die Funktionen stimmen überein. Die Funktion f(x) = x2 + 1 ist achsensymmetrisch zur y-Achse.
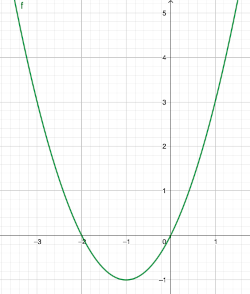
Ist f(x) = x2 + 2x achsensymmetrisch?
- Zuerst muss f(-x) berechnen werden: f(-x) = (-x)2 + 2(-x) = x2 – 2x
- Anschließend werden f(-x) und f(x) verglichen: f(-x) = x2 – 2x ungleich x2 + 1 = f(x)
- Die Funktionen stimmen nicht überein. Die Funktion f(x) = x2 + 2x ist nicht achsensymmetrisch zur y-Achse.
Symmetrieverhalten einfach erklärt: Achsensymmetrie und Punktsymmetrie
- Achsensymmetrie bildet sicher das bekannteste Symmetrieverhalten ab.
- Daneben gibt es aber unter anderem noch die Punktsymmetrie, auch Punktspiegelung genannt.
- Einfach gesagt spiegelt sich eine punktsymmetrische Funktion nicht an einer Geraden wie bei der Achsensymmetrie, sondern an einem Punkt.
- Während man bei Achsensymmetrie die (meistens) die Symmetrie zur y-Achse berechnet, betrachtet man bei Punktsymmetrie die Symmetrie zum Ursprung.
Wenn -f(x) = f(-x) gilt, ist eine Funktion achsensymmetrisch zum Ursprung.
Punktsymmetrie kommt wie Achsensymmetrie auch bei Figuren vor. Dabei wird die Figur an einem Punkt gespiegelt und es entsteht eine umgedrehte Kopie der Originalfigur.
Wenn du noch weitere Informationen zum Symmetrieverhalten von Figuren nachlesen möchtest, dann klicke einfach hier.
Symmetrieverhalten üben – Aufgabenblätter und Quiz
In diesem Abschnitt haben wir Aufgaben zum Ausdrucken für dich bereitgestellt. Mit dem Quiz kannst du dein Achsensymmetrie-Wissen sofort testen.
Achsensymmetrie in der Grundschule
- Wenn das Thema Achsensymmetrie im Matheunterricht in der Grundschule behandelt wird, handelt es sich in der Regel um das Spiegeln von Figuren.
- Wir haben dafür ein Aufgabenblatt zum Ausdrucken zusammengestellt, dass von Grundschüler*innen bearbeitet werden kann. So sind diese perfekt auf die nächste Unterrichtsstunde vorbereitet.
PDF-Datei: Achsensymmetrie PDF
Achsensymmetrie zur y-Achse beweisen
- In der weiterführenden Schule wird das überwiegend das Symmetrieverhalten von Funktionen und nicht mehr das von Formen betrachtet.
- Aus diesem Grund haben wir 3 Aufgaben zusammengestellt, in denen du berechnen musst, ob die Funktion achsensymmetrisch ist oder nicht.
- Wie du dabei vorgehen kannst, haben wir dir bereit im Abschnitt “Symmetrie zur y-Achse – Was du wissen musst!” gezeigt. Gucke dir die Vorgehensweise gerne nochmal an, bevor du anfängst zu rechnen.
Klicke einfach auf das + für die Lösung.
Ist f(x) = x^2 - 3 achsensymmetrisch?
- f(-x) = (-x)2 – 3 = (-x)*(-x) – 3 = x2 – 3
- f(-x) = x2 – 3 = f(x)
- Achsensymmetrisch zur y-Achse!
Ist f(x) = 2x^2 achsensymmetrisch?
- f(-x) = 2(-x)2 = 2 (-x)*(-x) = 2x2
- f(-x) = 2x2 = f(x)
- Achsensymmetrisch zur y-Achse!
Ist f(x) = 2x^2 + 3x - 1 achsensymmetrisch?
- f(-x) = 2(-x)2 + 3(-x) – 1 = 2x2 – 3x -1
- f(-x) = 2x2 – 3x -1 ungleich 2x2 + 3x – 1 = f(x)
- Nicht achsensymmetrisch zur y-Achse!
Hier auch als PDF-Datei: Achsensymmetrie zur y-Achse beweisen PDF
Symmetrieverhalten – Richtig oder falsch?
In diesem Quiz kannst du dein Wissen zum Thema Achsensymmetrie testen.
Entscheide für jede Aussage, ob diese richtig oder falsch ist.
Ergebnisse
#1. Die Achse, an der eine Figur gespiegelt wird, heißt Punktachse.
#2. Achsensymmetrie wird auch Spiegelsymmetrie genannt.
#3. Ein Quadrat hat 4 Symmetrieachsen.
#4. Ein gleichschenkliges Trapez hat 2 Symmetrieachsen.
#5. Ein Kreis hat unendlich viele Symmetrieachsen.
#6. Bei Funktionen wird die Symmetrie zur x-Achse nachgewiesen.
#7. Wenn f(x) = f(-x) gilt, ist eine Funktion achsensymmetrisch zum Ursprung.
#8. Punktsymmetrische Funktionen werden an einem Punkt gespiegelt.
#9. Wenn f(x) = f(-x) gilt, ist eine Funktion achsensymmetrisch zur y-Achse.
Noch mehr Hilfe im Fach Mathematik bekommst du auch bei unserer Mathe Nachhilfe. Unsere erfahrenen Tutoren sind sowohl vor Ort als auch Online flexibel für dich da!
Schau einfach mal vorbei und werde Teil des Nachhilfe-Teams.
Hat dir der Artikel gefallen? Hinterlasse gerne einen Kommentar!