4,87 von 5 Sterne
Loading...
Mathe ist in vielen Hinsichten schwer zu verstehen. Vor allem beim Thema Logarithmus ist das der Fall.
Doch zum Glück bist du auf diesen Artikel gestoßen, der dir alles leicht verständlich erklären wird. Somit kannst du in den nächsten Mathestunden mit diesem Wissen glänzen:
- Regeln
- Logarithmusgesetze anwenden und berechnen
- Logarithmusfunktionen erkennen und beschreiben
Also lasst uns anfangen!
Was ist ein Logarithmus?
Du kennst sicherlich schon Gleichungen aus der Potenzrechnung: 
Nehmen wir das Beispiel 
Auf den ersten Blick ist es nicht gleich erkennbar, welcher Wert für x eingesetzt werden muss. Diese Aufgabe übernimmt der Logarithmus. Die Schreibweise lautet folgendermaßen:
für unser Beispiel: 
Die 4 muss also dreimal mit sich selbst multipliziert werden, damit 64 rauskommt.
Merke: 
Mit Hilfe des Logarithmus wird eine Zahl x berechnet, mit dem die Basis b potenziert werden muss, um das Ergebnis a zu erhalten
weitere Beispiele:
Vorsicht: Logarithmen sind nur für positive Zahlen definiert. Zusätzlich darf die Logarithmusbasis b nicht gleich 1 sein
Auch der Logarithmus von 0 ist nicht definiert
Logarithmusgesetze – Was muss ich beachten?
Es gibt einige Logarithmus Regeln, die dir helfen, den Logarithmus berechnen zu können. Diese haben wir für dich im Folgenden zusammengefasst.
Produkt
Wenn du in einem Logarithmus ein Produkt x*y zu stehen hast, kannst du es ganz einfach in eine Summe umschreiben. Das Umschreiben funktioniert in beide Richtungen. Dies gilt auch für die nachfolgenden Regeln.
Merke: 
Beispiel: 
Quotienten
Ist innerhalb des Logarithmus ein Bruch, so kannst du diesen durch eine Differenz der Logarithmen ausdrücken. Der Nenner wird folglich vom Zähler abgezogen.
Merke: 
Beispiel: 
Potenz
Falls du auf eine Potenz stößt, kann diese leicht umgeschrieben werden. Der Exponent wird aus dem Logarithmus herausgezogen und mit diesem dann multipliziert.
Merke: 
Beispiel: 
Wurzel
Eine Wurzel begegnet dir innerhalb des Logarithmus? Kein Problem, multipliziere einfach den Wurzelexponent als Kehrwert mit dem Logarithmus.
Basiswechsel
Falls man eine bestimmte Basis haben will, kann dies mithilfe des Logarithmus Basiswechsel getan werden.
Merke: 
Beispiel: 
Übersicht Logarithmusregeln
Regeln | Formel | Beispiel |
Produkt |  |  |
Quotient |  |  |
Potenz |  |  |
Wurzel | logb(y√x)=1/푦⋅logb (푥) | log2(3√512)=1/3⋅log2(512)=1/3⋅9=3 |
Basiswechsel |  |  |
Besonderheiten Logarithmus
Neben dem allgemeinem Logarithmus, gibt es einige besondere Logarithmen mit bestimmten Zahlen als Basis b. Diese Besonderheiten haben einen großen Stellenwert. Deswegen werden sie im Folgenden näher erklärt.
dekadischer Logarithmus
Der dekadische Logarithmus beschreibt Logarithmen zur Basis 10. Meist wird die Basis weggelassen log oder noch weiter verkürzt zu lg.
Merke: 
Beispiel: 
natürlicher Logarithmus
Ist die Basis eines Logarithmus die Eulersche Zahl e, nennt man ihn natürlicher Logarithmus. Die Schreibweise für natürliche Logarithmen lautet ln.
Merke: 
Beispiel: 
Logarithmusfunktion – so sieht sie aus
Die allgemeine Formel für die Funktion ist folgendermaßen: 
(“y ist gleich Logarithmus von x zur Basis b)
Die Exponentialfunktion ist die Umkehrfunktion.
Eigenschaften
Die Logarithmusfunktion der Form verläuft durch den Punkt P (1/0) und ausschließlich im ersten und vierten Quadranten
Definitions- und Wertebereich
Da Logarithmen nur für positive Werte definiert ist, entspricht der Definitionsbereich nur den positiv reellen Zahlen.
Der Wertebereich hingegen entspricht den gesamten reellen Zahlen.
Monotonie
Die Logarithmusfunktion ist streng monoton. Ob streng monoton fallend oder streng monoton steigend hängt von der Basis b ab.
Merke : 0<b<1 -> streng monoton fallend
b>1 streng monoton steigend
Zudem besitzt die Logarithmusfunktion eine einzige senkrechte Asymptote, welche mit der y-Achse übereinstimmt. Das heißt die y-Achse wird nicht geschnitten.
Darstellung
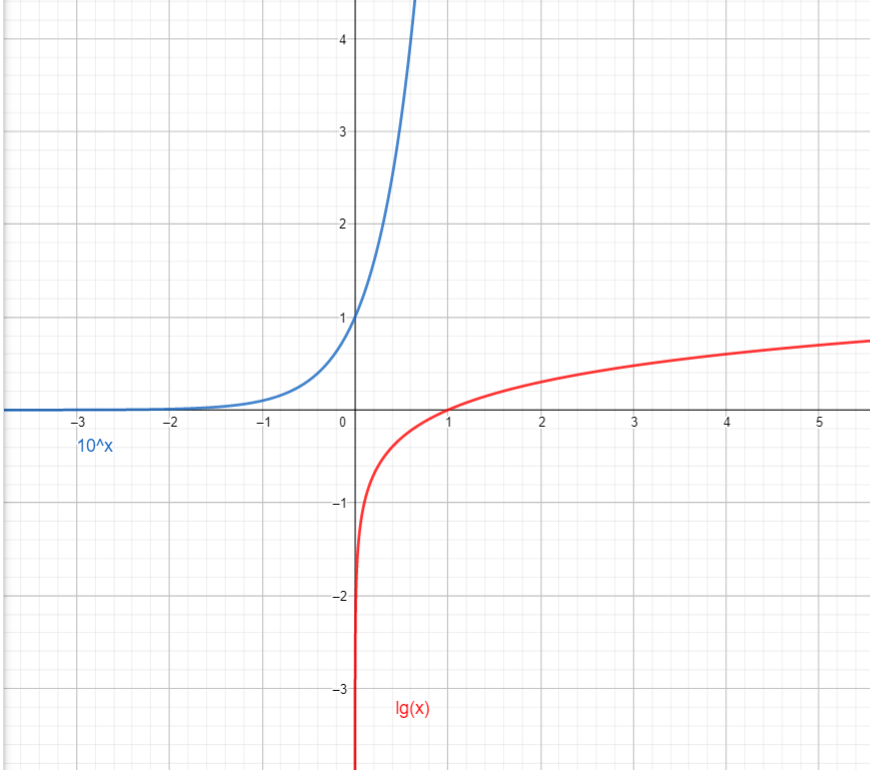
Hier siehst du einmal die Exponentialfunktion 10x in blau und die dazugehörige Umkehrfunktion in rot: Die Logarithmusfunktion lg(x).
Wie du siehst, verläuft die Logarithmusfunktion genau durch den Punkt P (1/0). Außerdem stellt d die y-Achse eine Asymptote dar.
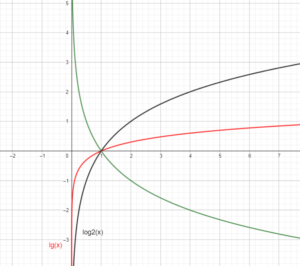
In der folgenden Abbildung sind verschiedene Varianten der Logarithmusfunktion zu sehen.
Die Funktionen lg(x) und log2(x) verlaufen streng monoton steigend. Der Grund dafür ist die Basis. Diese ist in beiden Fällen < 1 und somit ist das Monotonieverhalten monoton steigend. Hingegen besitzt die Funktion log0,5(x) eine Basis > 1. Deswegen verläuft sie monton fallend.
Wie bei den Eigenschaften bereits besprochen, verlaufen all diese Funktionen durch den Punkt P(1/0). Dieser Punkt ist gleichzeitig auch die Nullstelle für die Funktionen.
Aufgaben für Logarithmen – So können sie lauten
a) 2x = 32
b) 3x = 27
c) 49x = 7
Lösung
a) x = 5
b) x = 3
c) x = 0,5
a) log4(x) = 3
b) logx(8) = 3
c) lg(100) = x
Lösung
a) x = 64
b) x = 2
c) x = 2
a) log3(a) + log3(b)
b) ln(x³)
c) lg(a) – 3lg(b)
Lösung
a) log3(a*b)
b) 3*ln(x)
c) lg(a/3b)
Bewerte diesen Artikel
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung hinterlässt. Vielen Dank! ?
4,87 von 5 Sterne
Loading...
Kennst du schon unsere Artikel zur Kettenregel zur Quotientenregel oder eines Kreuzproduktes?
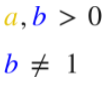
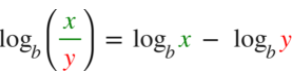
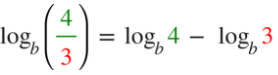
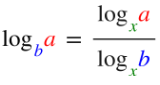
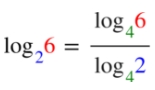
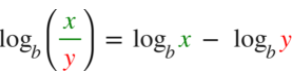
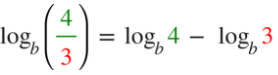
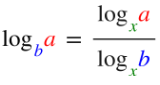
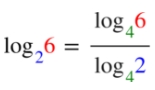
Der Artikel ist sehr gut. Was man verbessern könnte ist, dass man bei den Lösungen der Aufgaben auch noch der Rechnungsweg aufschreibt, damit man weiss was man nicht richtig gemacht hat, falls man es falsch gerechnet hat.
Danke für die Erläuterung.
Mit der Log-Regel bei Wurzeln habe ich Schwierigkeiten. Nach dem Vorziehen des Wurzelexponenten bleibt im log eine Wurzel??
Log’b'(4^1/2) also Quadratwurzel = 1/2* log’b'(Wurzel aus 4) .
Die Regel kann doch so nicht richtig sein….
VG
Hey Tk,
vielen Dank für deinen Kommentar! Du hast recht, die Wurzel verfällt nach dem Vorziehen des Kehrwertes. Ist verbessert 🙂