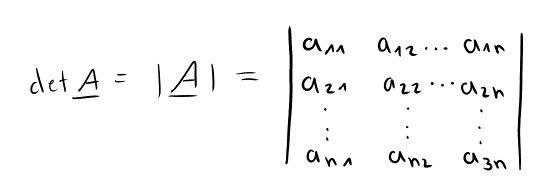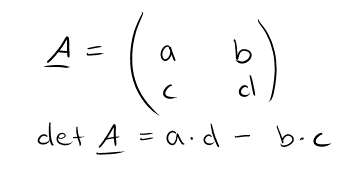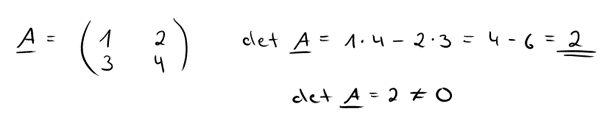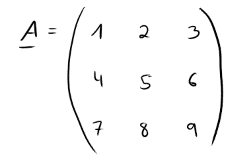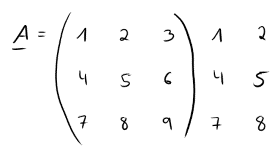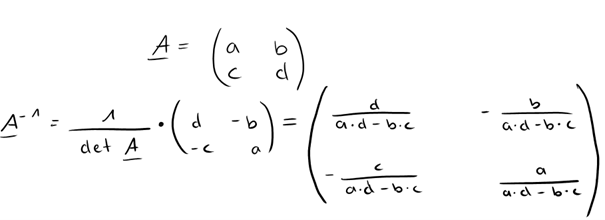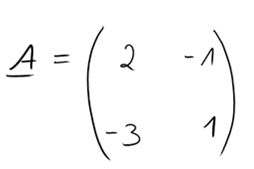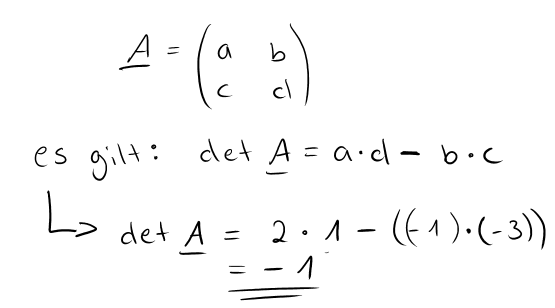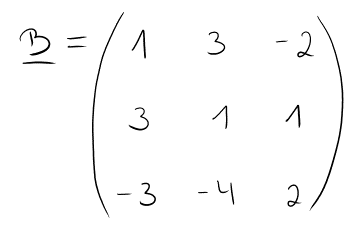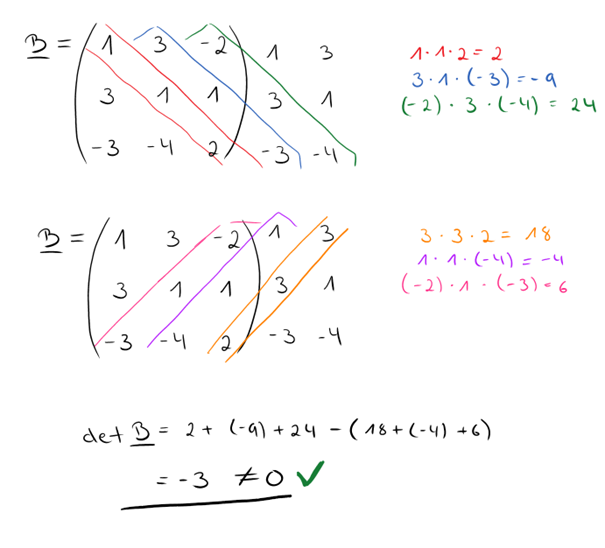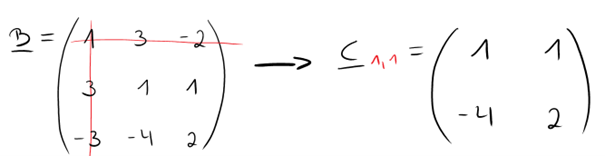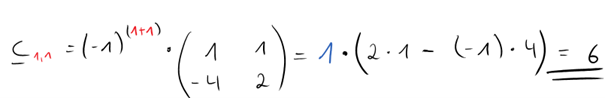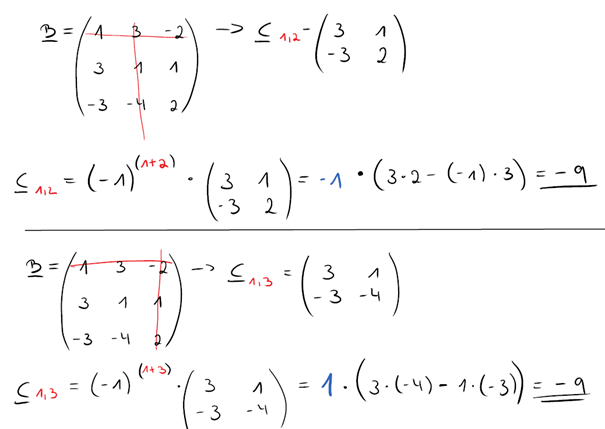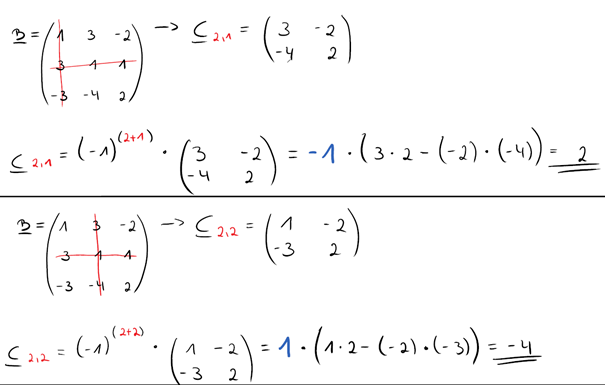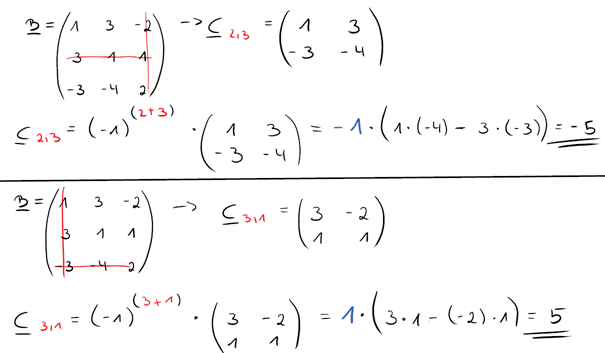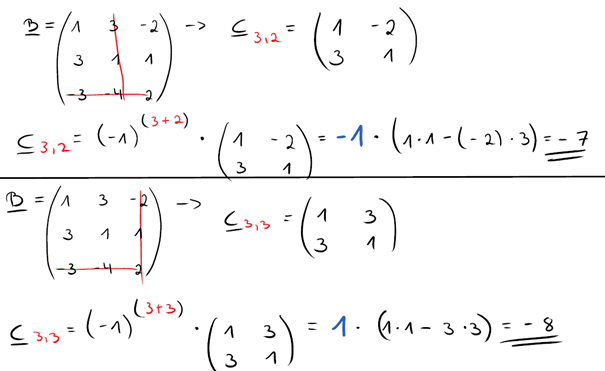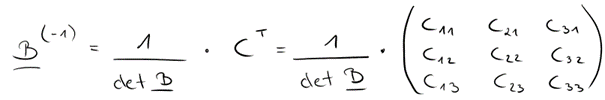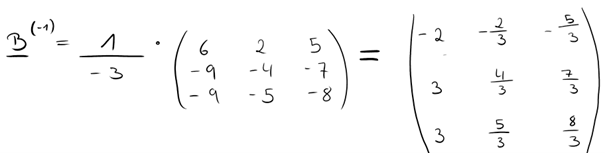3,83 von 5 Sterne
Loading...
Die inverse Matrix (auch Inverse oder Kehrmatrix genannt) ist ein am Anfang eher unübersichtliches Thema. Aber mach dir da keine Sorgen, genau aus diesem Grund gibt es den Artikel für dich!
Ich werde dir hier zeigen…
… wann du die inverse Matrix berechnen kannst,
… eine Erklärung zu Determinanten und wie man sie berechnet (mit Beispiel)
… die Berechnung der inversen Matrix anhand von Beispielen (mit 2×2 und 3×3 Matrizen).
Danach wird dir das Thema nicht mehr so schwer fallen.
Bevor es los geht, noch eine kurze Info:
Wir haben einen Artikel über Matrizen im Allgemeinen verfasst. Schau dort gerne mal vorbei, wenn du noch Hilfe brauchen solltest, bei anderen Themen.
Wann kann ich eine Matrix invertieren?
Ganz wichtig: Es sind NUR quadratische Matrizen invertierbar. Aber: das bedeutet nicht, dass für jede quadratische Matrix auch eine inverse Matrix existiert.
Das hängt dann von der Determinante ab: ist die Determinante gleich Null, gibt es keine inverse Matrix. Also muss als Voraussetzung die Determinante immer ungleich Null sein.
Wir machen dann gleich mit den Determinanten weiter. Da werde ich dir alles nochmal ausführlicher erklären. Bist du schon Fit in dem Thema, dann kannst du gerne gleich zur Berechnung der Inversen weiter gehen.
Determinanten – Grundlagen und Berechnung (mit Beispielen)
In diesem Abschnitt werden die Determinanten nochmal genauer ausgeführt. Da sie als Voraussetzung für die inverse Matrix berechnet und geprüft werden müssen, solltest du dich mit dem Thema auskennen.
Jeder quadratischen Matrix (Typ (n,n)) kann eine Zahl – oder auch Determinante – zugeordnet werden. Die Schreibweise für die Determinanten sieht folgendermaßen aus:
Ich werde in unseren Beispielen die erste Variante anwenden.
Die Berechnung erfolgt auf unterschiedliche Art und Weise – je nach dem, welchen Typ die Matrix besitzt.
Hat eine Matrix zwei Zeilen und zwei Spalten, ist sie vom Typ (2,2). Die Zeilenzahl kommt zuerst und die Spaltenzahl als Zweites.
Schauen wir uns die Berechnung mal zusammen an. Ich habe diese aufgeteilt, nach dem Wert des n.
n = 1 — die Determinante ist der Wert des Elements a11 (also oben links in der Ecke)
n = 2 — quadratische Matrix vom Typ (2,2) gegeben.
Die Berechnung für die Determinante sieht so aus:
Wir berechnen die mal zusammen, anhand eines kleinen Beispiels:
Wie du siehst, ist bei Matrizen vom Typ (2,2) die Berechnung der Determinante wirklich noch simpel.
Zu Beginn habe ich ja gesagt, dass nicht jede quadratische Matrix automatisch auch eine inverse Matrix besitzt. Es muss immer die Voraussetzung geprüft werden (Determinante ungleich Null) und erst wenn sie gegeben ist, besitzt die Matrix auch eine Inverse.
In unserem Beispiel existiert also eine inverse Matrix, weil die Voraussetzung erfüllt wurde.
n = 3 — hier werde ich die “Regel von Sarrus” anwenden, um die Determinante zu berechnen.
Die Berechnung verläuft etwas komplizierter ab, als bei den 2×2 Matrizen. Aber das macht nichts, ich werde dir alles Schritt-für-Schritt erklären.
Gegeben ist die folgende Matrix:
Laut der Regel von Sarrus werden nun die ersten beiden Spalten nochmal rechts neben die Matrix geschrieben:
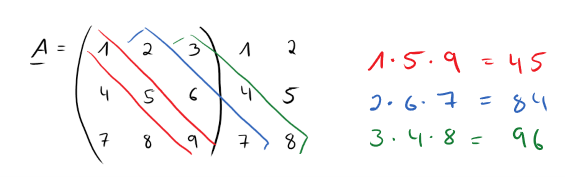
Als nächstes werden Produkte gebildet (jeweils drei – durch schräge Linien – verbundene Zahlen). Der Startpunkt ist oben links in der Ecke (also bei der 1).
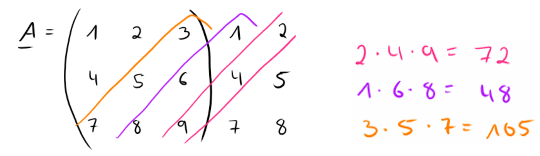
Jetzt das Ganze nochmal von der “anderen Seite”. Du startest also rechts oben in der Ecke (bei der 2):
Der letzte Schritt besteht nun darin, Summen aus den Produkten zu bilden und die zweite Rechnung von der ersten abzuziehen. Das heißt:
45 + 84 + 96 – (72 + 48 + 105) = 0
Mit dieser Matrix haben wir nun genau den Fall erreicht, in der die Matrix keine Inverse besitzt. Wie du sehen kannst, kommt als Endergebnis Null raus – die Voraussetzung ist also nicht erfüllt worden.
Also: bei diesem Beispiel hier besitzt die Matrix keine Inverse, weil die Voraussetzung nicht erfüllt wurde.
n > 4 — hierfür wird der Entwicklungssatz von Laplace angewendet.
Da dies aber den Umfang sprengen würde, werden wir den hier nicht nochmal extra anschneiden.
Berechnung der inversen Matrix mit Beispielen (2×2 und 3×3)
Rechenregeln im Überblick
Wie bei allem anderen auch, gibt es für die inverse Matrix ebenfalls bestimmte Regeln, die befolgt werden müssen. Die Rechenregeln der inversen Matrix als Übersicht kannst du dir auch gerne herunterladen, falls du es brauchen solltest.
Wie du in der Übersicht erkennen kannst, ist die Schreibweise der inversen Matrix das A hoch -1.
Beispiel 1 – Matrix vom Typ (2,2)
Fangen wir nun mit dem ersten Beispiel an. Um klein anzufangen werden wir mit einer Matrix vom Typ (2,2) beginnen.
Was du hier unten siehst, ist das grundlegende Berechnungsschema für die inverse Matrix.
Jetzt rechnen wir das Ganze mal Schritt-für-Schritt zusammen aus.
Gegeben sei folgende Matrix vom Typ (2,2):
Zuerst müssen wir die Voraussetzung prüfen (Determinante ungleich Null).
Deshalb fangen wir damit an, die Determinante unserer Beispielmatrix zu berechnen. Da es sich hierbei um eine Matrix vom Typ (2,2) handelt, ist die Berechnung recht simpel:
Wie du siehts, ist die Determinante hier ungleich Null. Also ist die Voraussetzung erfüllt und wir wissen, dass es eine inverse Matrix gibt.
Im nächsten Schritt wollen wir die inverse Matrix nun berechnen.
Hierfür nehmen wir uns das Berechnungsschema für 2×2 Matrizen zur Hand und setzen die Zahlen ein.
Da du das Berechnungsschema schon hast, würde ich dich bitten, die Inverse mal selbst zu berechnen.
Wie gesagt: das Schema ist da, du musst nur noch die Zahlen einsetzen und die Ergebnismatrix berechnet. Also nimm dir Zettel und Stift und versuch es mal selbst.
Die Lösung findest du hier unten zum Aufklappen.
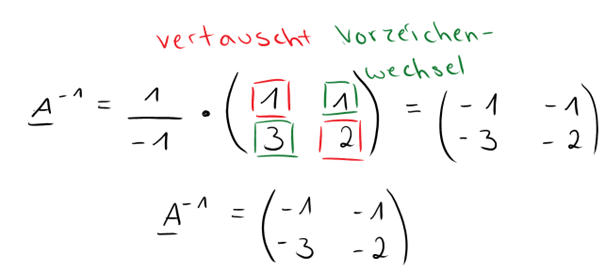
Lösung - inverse Matrix (2x2)
Hervorragend, das ist es schon gewesen!
Wie du siehst, ist die Berechnung bei den 2×2 Matrizen wirklich noch einfach gehalten.
Im nächsten Abschnitt werden wir uns die 3×3 Matrizen mal anschauen, die einen wesentlich komplexeren Rechenweg haben.
Aber mach dir nichts draus! Wir machen das zusammen, Schritt-für-Schritt.
Beispiel 2 – Matrix vom Typ (3,3)
Wie versprochen geht es jetzt weiter mit einer Matrix vom Typ (3,3) und das Berechnen ihrer inversen Matrix.
Ich werde hier die Inverse mithilfe der sogenannten Adjunkte berechnen.
Wir haben folgende Matrix gegeben:
Der nächste Schritt ist, die Determinante der Ausgangsmatrix B zu berechnen.
Wie das geht, haben wir ja schon im Kapitel über die Determinanten besprochen. Falls du da nochmal schauen musst, weißt du, wo es steht.
Die gesamte Rechnung lautet also:
Wie du sehen kannst, ist die Voraussetzung erfüllt und wir wissen, dass unsere Matrix eine Inverse besitzt. Jetzt machen wir weiter mit der Berechnung.
Der nächste Schritt ist, die erste Teilmatrix zu bestimmen. Dafür wird eine Zeile und eine Spalte aus der Ausgangsmatrix gestrichen.
Für unsere Matrix würde die erste Teilmatrix dann folgendermaßen aussehen:
Kleine Notiz am Rande: die Determinante der Teilmatrix wird Unterdeterminante genannt.
Als nächstes musst du die Determinante dieser Matrix berechnen. Dafür hast du (für alle Teilmatrizen) folgendes Rechenschema:
Die oben beschriebenen Rechenschritte müssen jetzt für ALLE Teilmatrizen ausgeführt werden (insgesamt neun Stück).
Ich habe dir hier eine Übersicht reingestellt, wie die Berechnung bei den restlichen Teilmatrizen abläuft.
Nun kommt der letzte Schritt. Hierfür nimmst du dir folgende Formel:
Und setzt die berechneten Werte ein, also:
- die Determinante unserer Ausgangsmatrix
- und alle Unterdeterminanten der restlichen Teilmatrizen in Matrixschreibweise
Jetzt musst du nur noch berechnen, indem du die Zahl vor der Matrix mit jedem Element einzeln multiplizierst.
Und zack! Schon haben wir unsere inverse Matrix berechnet:
Wie du siehst, ist das Ausrechnen schon eine aufwendigere Sache, als bei den 2×2 Matrizen.
Aus diesem Grund habe ich dir hier die gesamte Berechnung als PDF-Dokument nochmal dargestellt. Du kannst es dir also gerne herunterladen und es dir in Ruhe mal anschauen.
Zusammenfassung über die inverse Matrix
In diesem Artikel hast du gelernt, wie man die Determinante einer Matrix berechnet und wie die Berechnung einer inversen Matrix (bei 2×2 und 3×3 Matrizen) verläuft.
Wir merken uns also: zuerst muss die Determinante der Matrix berechnet werden. Ist diese ungleich Null, besitzt die Matrix auch eine Inverse und wir können beim nächsten Schritt weiter machen.
Je nach Typ der Matrix unterscheidet sich nun der weitere Weg der Berechnung. Bei der 2×2 Matrix ist sie noch sehr simpel, aber bei der 3×3 Matrix muss für jede Teilmatrix (insgesamt neun) die Unterdeterminante berechnet werden, alle zusammen dann als Matrixschreibweise formuliert in eine Formel eingesetzt werden und dann kommt die inverse Matrix raus.
Was sagst du zu unserem Artikel?
Ich hoffe, dass dir meine Berechnungsbeispiele dabei helfen konnten, das Thema besser zu verstehen. Schreib uns also einen Kommentar oder gib eine Bewertung ab, wie und ob dir der Artikel weiter helfen konnte. Vielen Dank!
3,83 von 5 SterneLoading...
