Subtrahieren – mit simplen Beispielen und Aufgaben

Subtrahieren, wie genau funktioniert das eigentlich? Hier erfährst du alles was du über das Subtrahieren wissen musst. Abziehverfahren und Ergänzungsverfahren, Begriffe der Subtraktion und wie du Brüche subtrahierst. 

Einfach erklärt mit :

• Beispielaufgaben zum Subtrahieren
• Regeln, die du kennen musst

Starten wir direkt!

Subtraktion – Was ist das ?

Die Subtraktion, auch Minusrechnung genannt ist einer der vier Grundrechenarten (Addition, Subtraktion, Multiplikation und Division).Unter einer Subtraktion versteht man das Abziehen einer Zahl von einer anderen.

Das Rechenzeichen für die Subtraktion ist das Minuszeichen. Außerdem ist das Gegenteil der Subtraktion die Addition.

Subtraktion Begriffe – diese solltest du kennen

Damit dir das Rechnen einfacher fällt, solltest du dir einmal im Klaren über die Begriffe sein.

Der Minuend

Als Minuend wird die Zahl bezeichnet, von der etwas abgezogen wird.

Der Subtrahend

Als Subtrahend wird die Zahl bezeichnet, die von der anderen Zahl abgezogen wird.

Die Differenz

Das Ergebnis der Subtraktion ist der Wert der Differenz. Die Differenz ist also ein Rechenausdruck, der den Minuend und den Subtrahend umfasst.

Subtraktion Beispiel Rechnungen:

Der Wert der Differenz kann auch in den negativen Bereich gehen, wenn nämlich der Subtrahend größer ist als der Minuend. Der Wert der natürlichen Zahlen kann also überschritten werden.

schriftliche Subtraktion – in einfachen Schritten

Wenn du mit höheren Zahlen rechnest, oder mehrere Subtrahenden hast, kannst du mit Hilfe von schriftlicher Subtraktion Aufgaben leichter lösen.

Subtraktionsverfahren

schriftliche Subtraktion – 2 verschiedene Verfahren

Bei der schriftlichen Subtraktion kannst du zwischen 2 Verfahren unterscheiden.:

• Ergänzungsverfahren
• Abziehverfahren

Beide Verfahren werden untereinander aufgeschrieben und wie folgt berechnet:

Das Ergänzungsverfahren

Bei dem Ergänzungsverfahren schaust du, wie viel du zum Subtrahenden hinzufügen musst, um den Minuenden zu erreichen.

Also was im Ergebnis hinzugefügt werden muss. Du rechnest jede Zahl Schritt für Schritt einzeln aus und gehst von hinten nach vorne vor.

Hier ein Beispiel zum Verständnis:

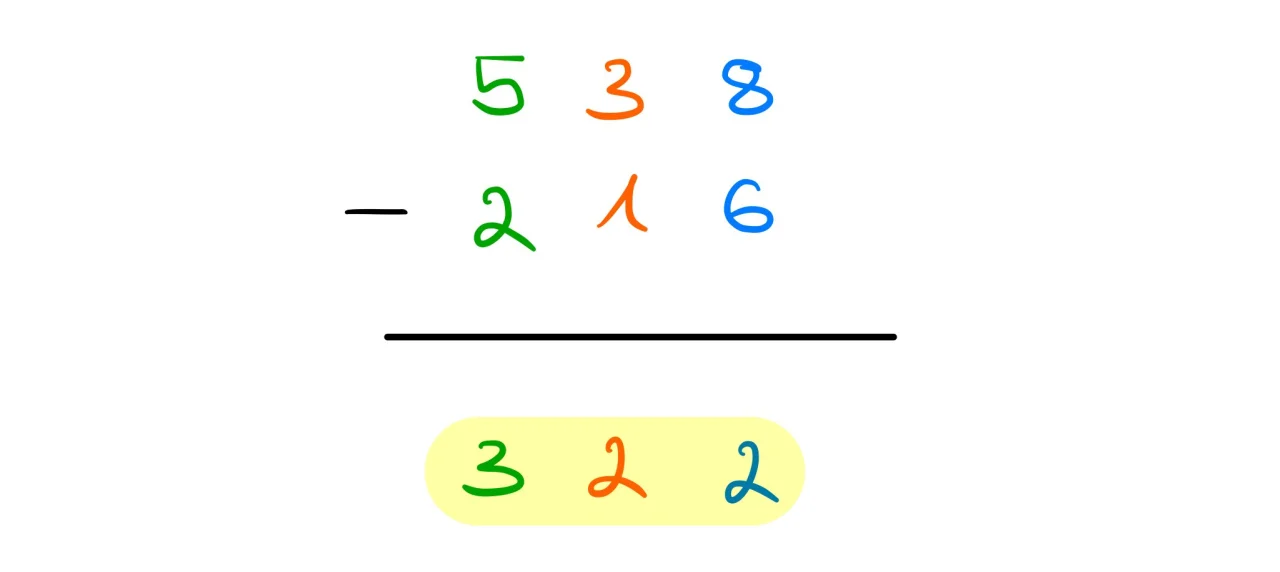
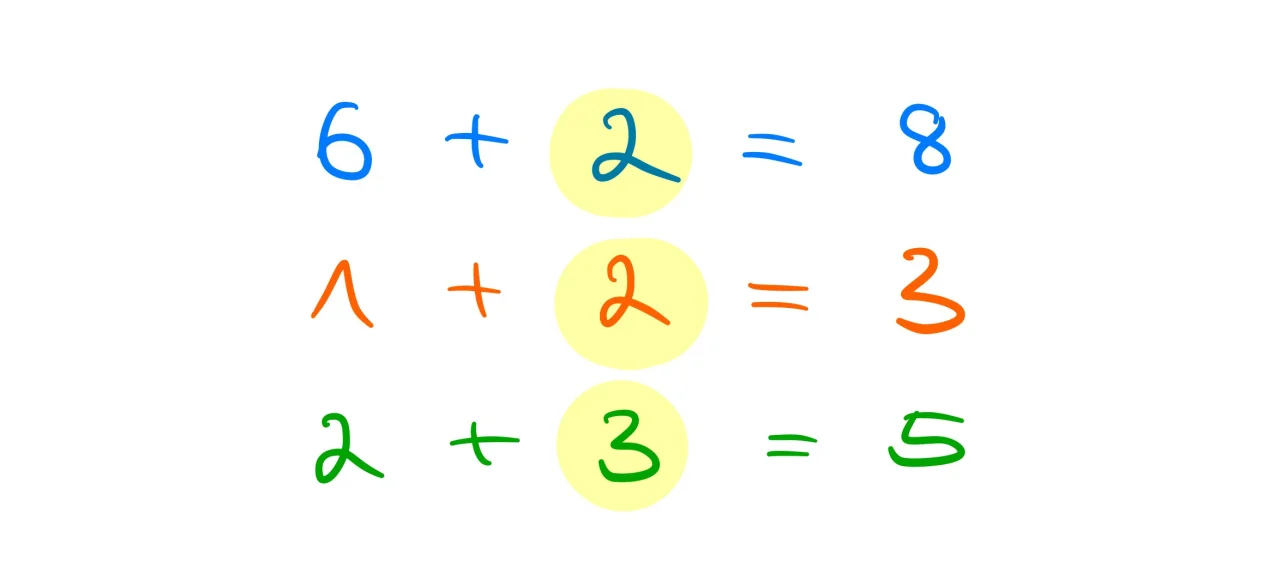
Das Abziehverfahren

Die Berechnung des Abziehverfahren erfolgt auch von hinten nach vorne.
Hier ziehst du jede einzelne Zahl des Subtrahenden von jeder einzelnen Zahl des Minuenden ab .

Hierzu ein Beispiel:

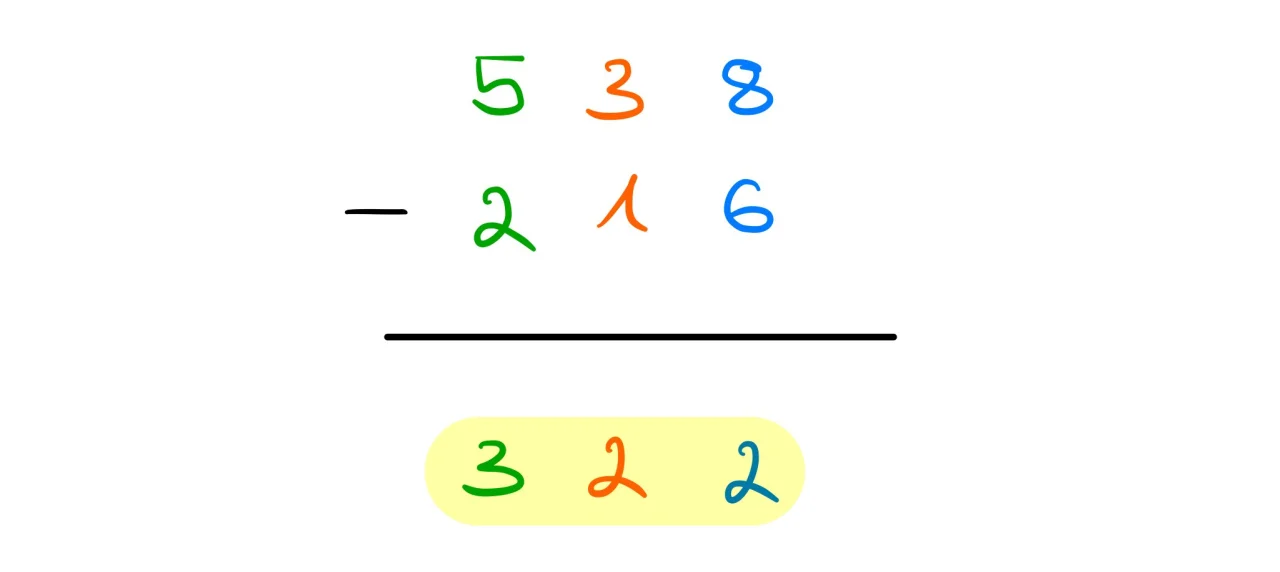
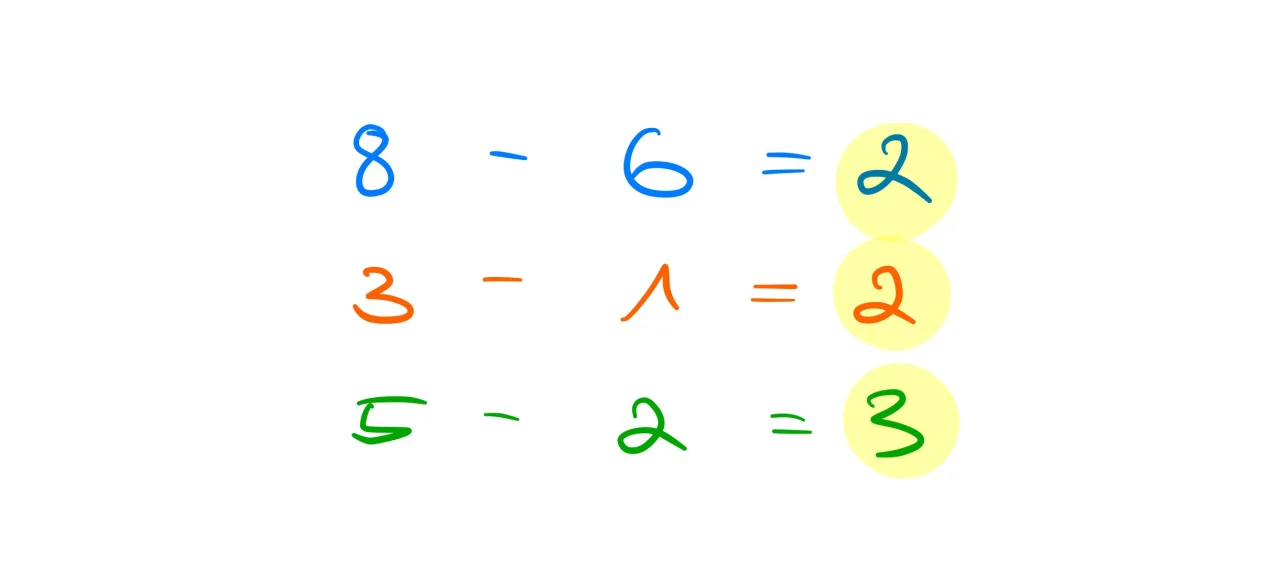
schriftliche Subtraktion Dezimalzahlen

Beide Verfahren funktionieren auch bei Dezimalzahlen (Kommazahlen). Es funktioniert genau gleich, nur dass du ein Komma an die entsprechende Stelle setzen musst.

Beispiel Subtraktion Dezimalzahlen

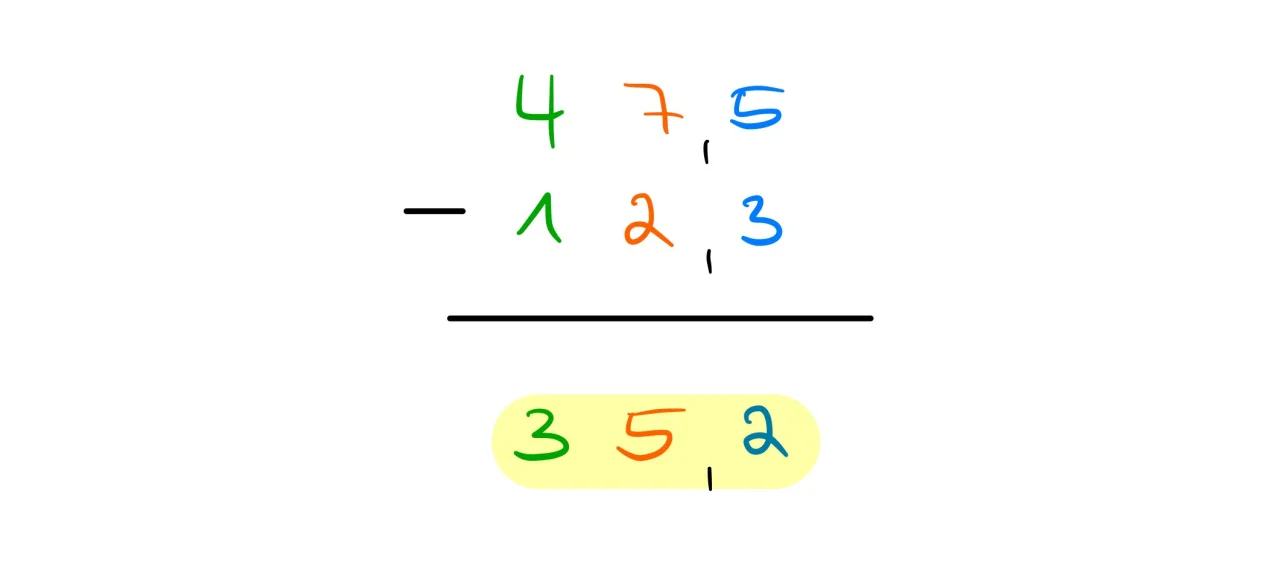
Subtrahieren – schriftliche Subtraktion mit Überschreitung

Beginnen wir mit einem Beispiel:

Berechnung mit dem Ergänzungsverfahren

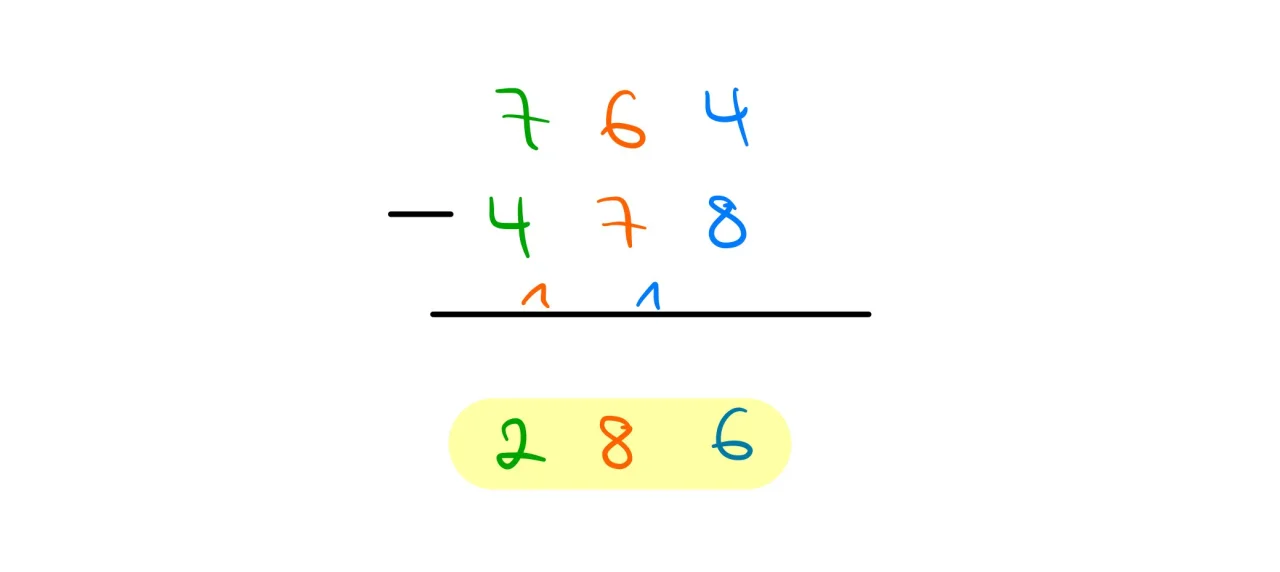
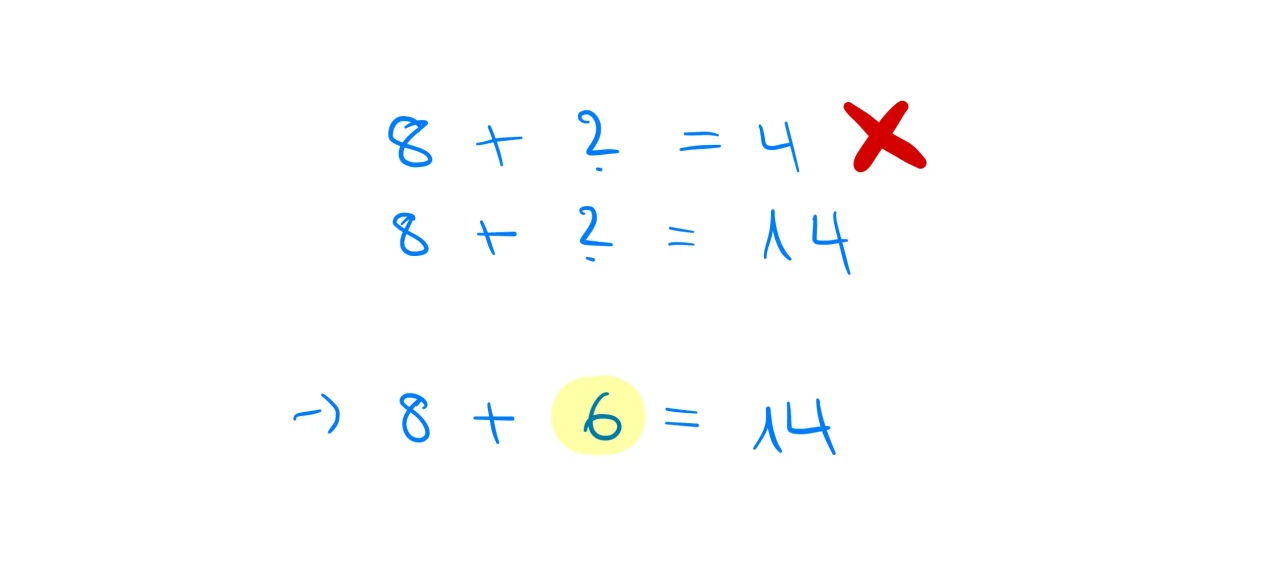
8 + ? = 4 funktioniert nicht. Deshalb fügst du einen Zehner hinzu und schreibst die 1 (die Überschreitung) klein in den Zehner Bereich dazu.

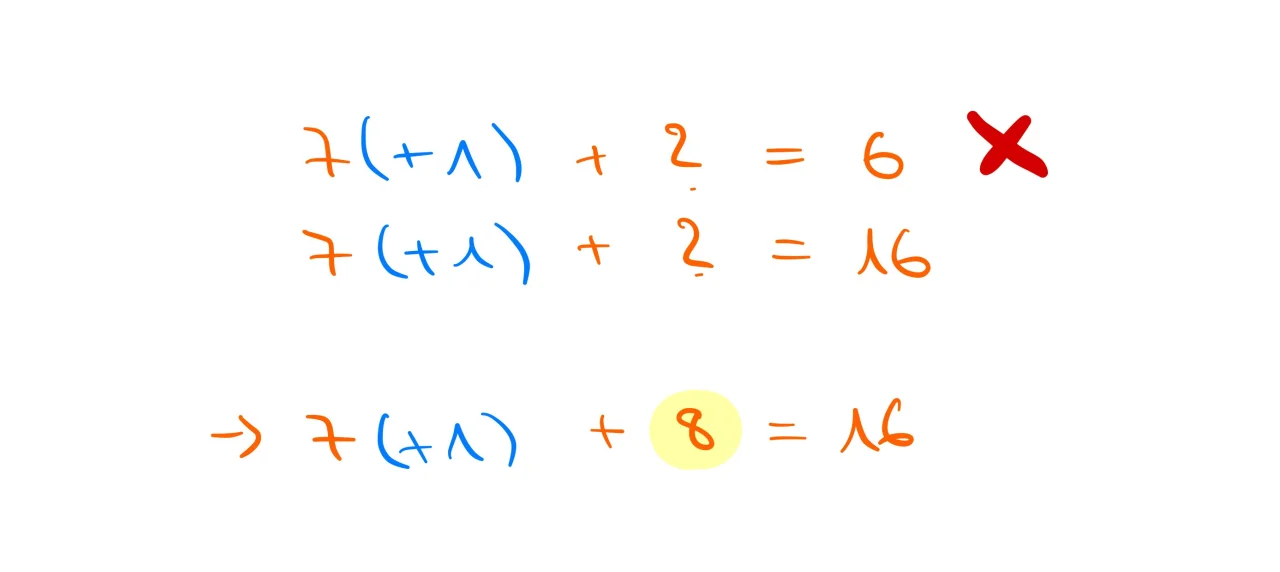
7 (+1) + ? = 6 funktioniert nicht. Deshalb fügst du einen Zehner hinzu und schreibst die 1 (die Überschreitung) klein in den Hunderter Bereich dazu.

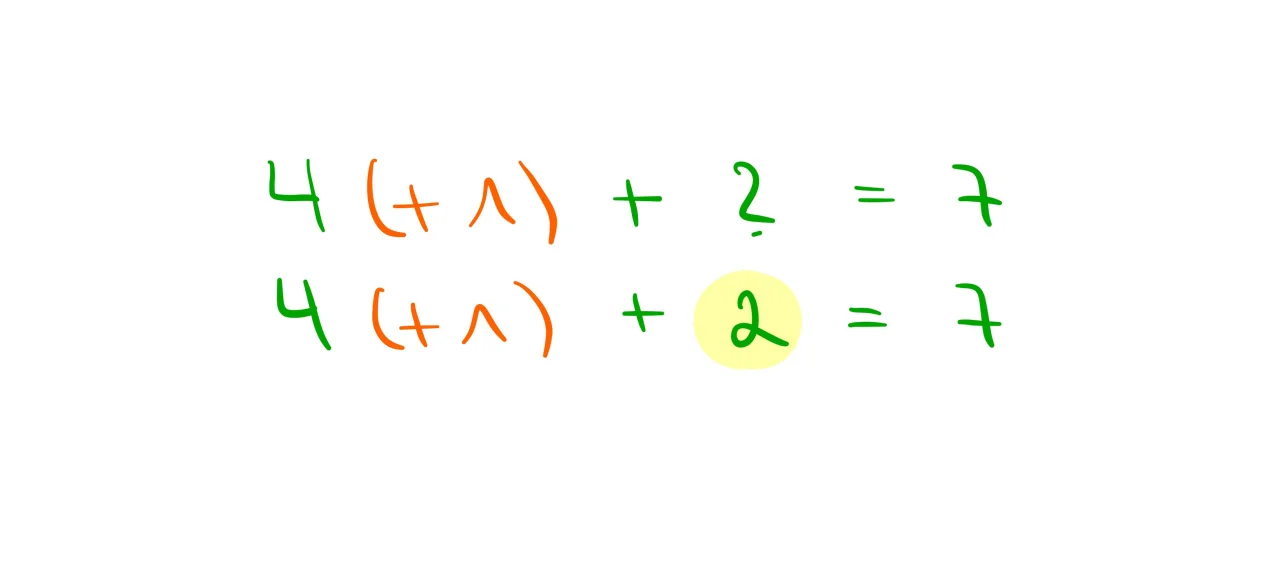
Berechnung mit dem Abziehverfahren

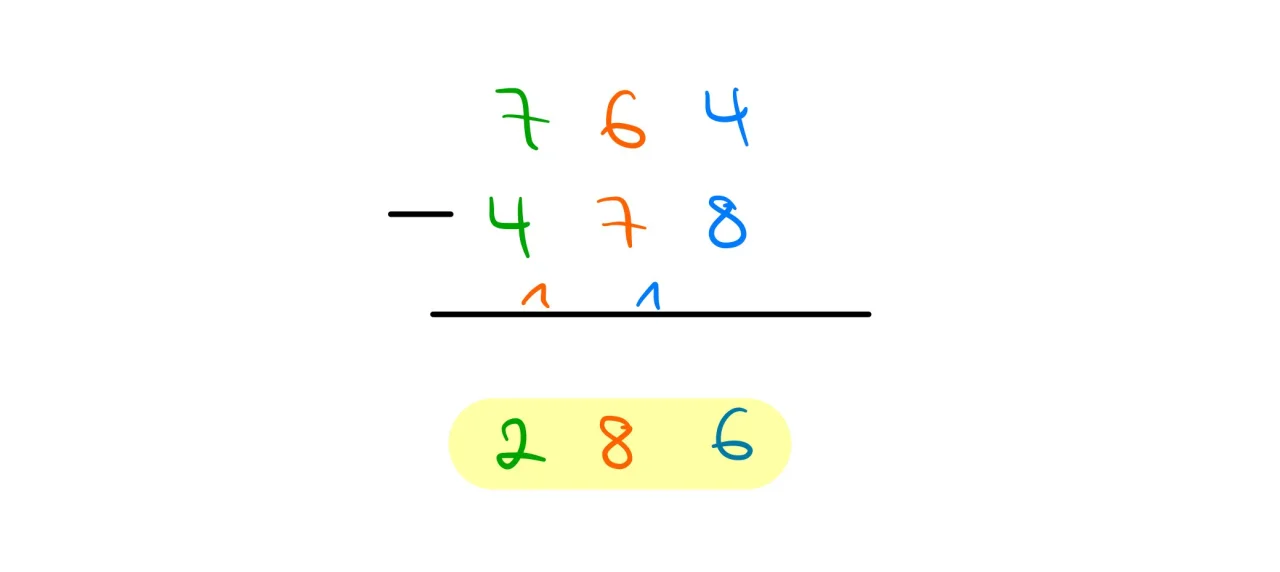
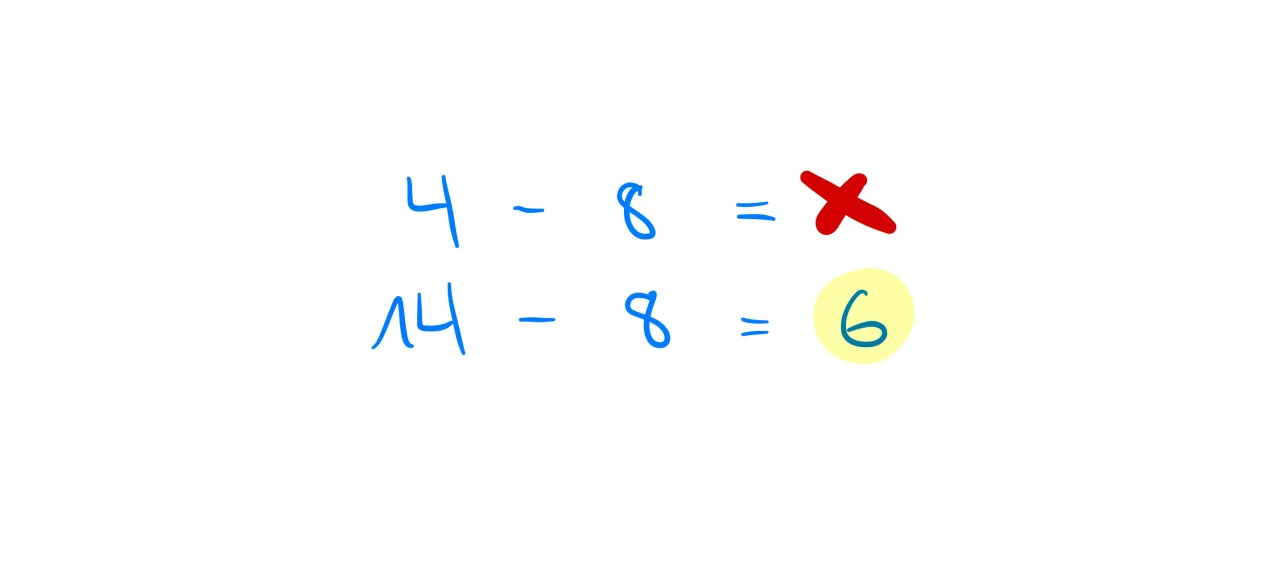
4 – 8 funktioniert nicht. Deshalb machen wir aus der 4 eine 14 und schreiben den Übertrag klein als 1 in den Zehnerbereich.

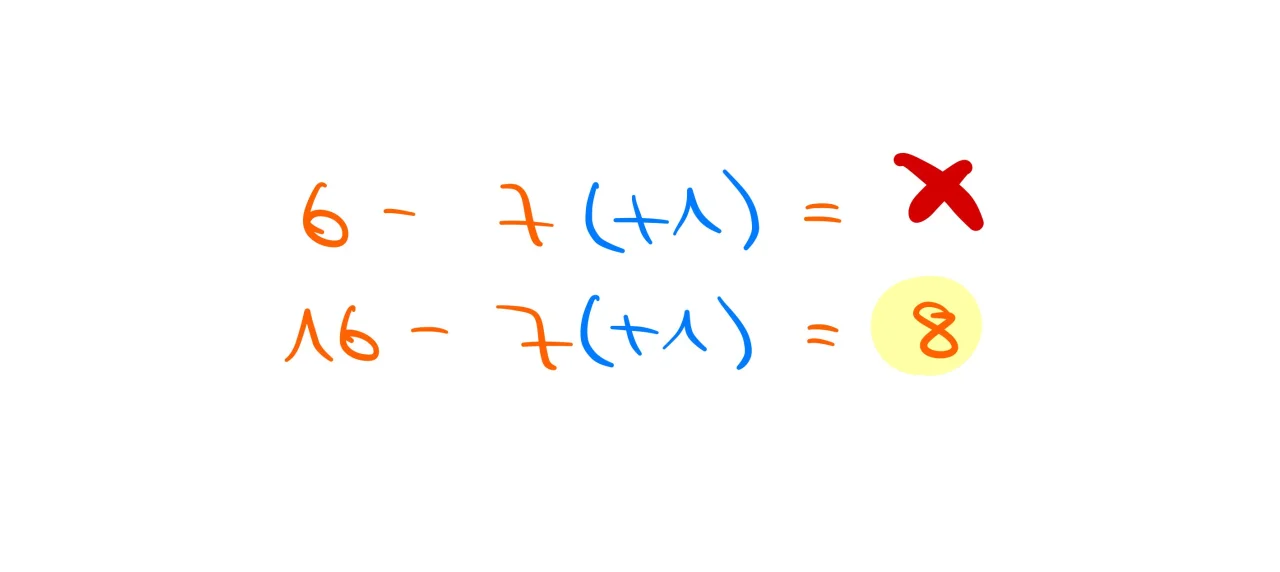
6 – 8 ( 7+1) funktioniert nicht. Deshalb machen wir aus der 6 eine 16 und schreiben den Übertrag klein als 1 in den Hunderterbereich.

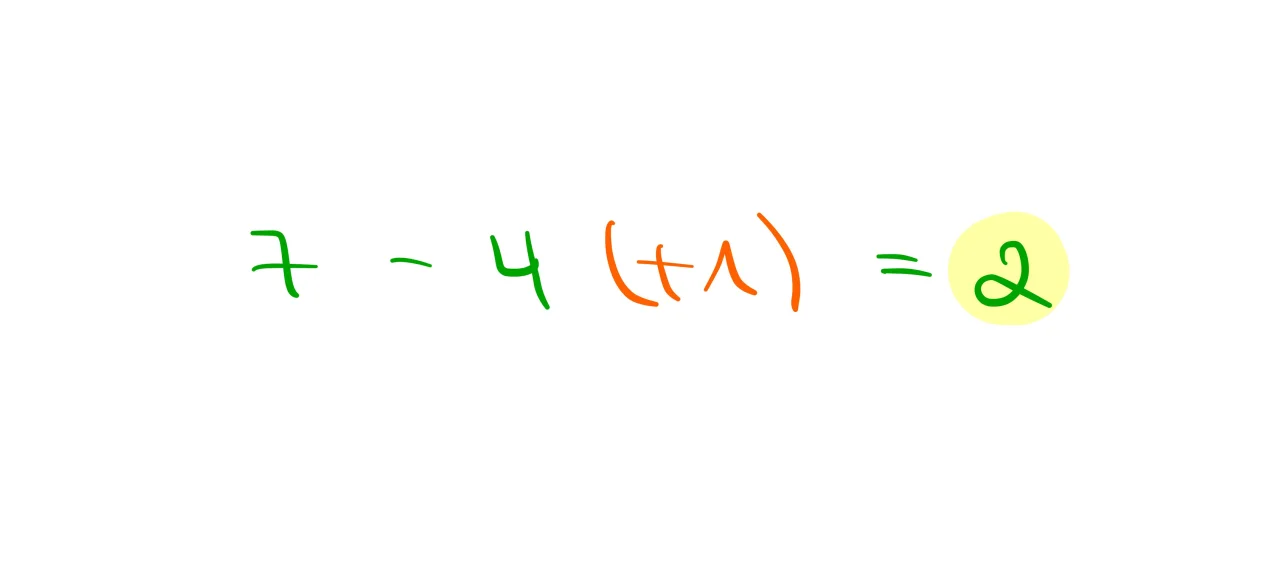
Brüche subtrahieren

Natürlich kannst du auch Brüche voneinander subtrahieren. Das erklären wir dir im nächsten Schritt.

Subtrahieren: Brüche mit dem selben Nenner

Haben zwei Brüche, die du voneinander subtrahierst den selben Nenner, subtrahierst du die Zähler voneinander und behältst die Nenner bei.

Hier ein Beispiel:

Subtrahieren: Brüche mit verschiedenen Nennern

Haben zwei Brüche, die du voneinander subtrahierst verschiedene Nenner, musst du die Brüche so erweitern, dass beide Brüche denselben Nenner haben.

Die neuen Nenner werden dann Hauptnenner genannt.

Im Anschluss kannst du die Zähler wieder voneinander abziehen.

Den Hauptnenner rechnest du aus, indem die die Nenner beider Brüche miteinander multiplizierst.

Hier ein Beispiel:

Subtrahieren – Aufgaben

Damit du dein Wissen noch einmal etwas vertiefen und testen kannst, berechne im nächsten Schritt die Aufgaben einmal selber. Um dein Ergebnis zu kontrollieren, klicke einfach auf das +!

Wenn du wissen möchtest, wie du Brüche miteinander addierst, schaue hier doch gerne vorbei!