4,14 von 5 Sterne
Loading...
Auf dieser Seite zeigen wir dir, wie du im Handumdrehen Umfang, Oberfläche, Volumen und Kreisfläche einer Kugel berechnen kannst.
Sieh dir alle Rechenwege im Detail an und übe das Gelernte mithilfe von Beispielaufgaben!
Was ist eine Kugel?
Die Kugel ist ein geometrischer Körper, der vollkommen rund ist. Sie besitzt also keine Ecken oder Kanten.
Alle Punkte der Oberfläche O haben somit den gleichen Abstand zum Mittelpunkt M der Kugel.
Stell dir vor, du würdest einen perfekt runden Kreis um einen festen Punkt in alle Richtungen rotieren. Dadurch erhältst du die Kugeloberfläche.
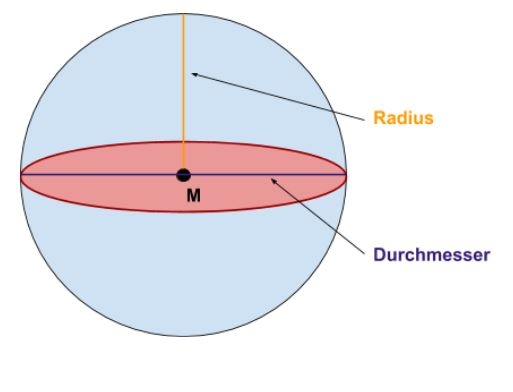
Radius und Durchmesser
Der Abstand von der Kugeloberfläche zum Mittelpunkt der Kugel wird als Radius r bezeichnet. Der Durchmesser d einer Kugel entspricht zweimal der Länge des Radius r:
r = ½ · d
d = 2 · r
Mit dem Radius (bzw. Durchmesser) und der Kreiszahl Pi kannst du ganz einfach Umfang, Oberfläche, Volumen und Kreisfläche berechnen!
Welche Formeln du hierfür benötigst, erfährst du in den nächsten Abschnitten.
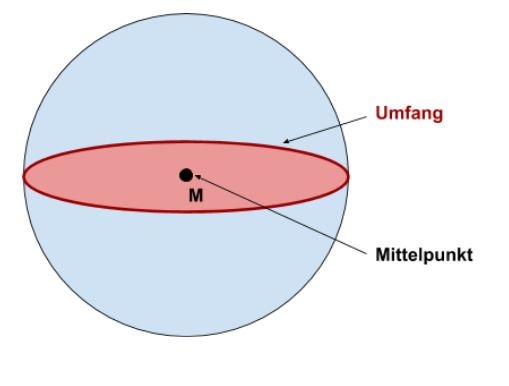
Umfang einer Kugel
Mit diesen Formeln lässt sich der Umfang U einer Kugel berechnen:
U = 2 · π · r
U = π · d
Nun bist du an der Reihe. Übe die Umfangsformel, indem du die folgenden Aufgaben bearbeitest!
Wie groß ist der Umfang einer Kugel mit dem Radius r = 4 cm?
U = 2 · π · r
U = 2 · π · 4 cm
U = 8 cm · π
U ≈ 25,133 cm
Der Umfang beträgt ca. 25,13 cm.
Wie groß ist der Umfang eines (perfekt runden) Balles, der einen Durchmesser von d = 9 cm hat?
Du hast den Durchmesser d der Kugel und kannst den Wert in die Formel einsetzen:
U = d · π
U = 9 cm · π
U ≈ 28,27 cm
Der Umfang beträgt ca. 28,27 cm.
Oberfläche einer Kugel
Die Oberfläche ist die Außenfläche der Kugel, also das, was du berühren kannst, wenn du eine Kugel in der Hand halten würdest. Mit dem Radius/Durchmesser und Pi kannst du ganz einfach die Oberfläche O einer Kugel berechnen.
O = 4 · π · r²
O = π · d²
Teste dein Wissen in den beiden folgenden Übungsaufgaben! Schau dir die Lösung an, falls du nicht weiterkommst.
Wie groß ist die Oberfläche eines Balles, der einen Radius von r = 11 mm hat?
Oberfläche Kugel berechnen: Einsetzen des Radius in die bekannte Formel:
O = 4 · π · r²
O = 4 · π · (11 mm)²
O = 4 · π · 121 mm²
O ≈ 1520,53 mm²
Die Oberfläche beträgt ca. 1520,53 mm².
Wie groß ist die Oberfläche der Kugel mit einem Durchmesser von d = 12 cm?
Den Wert von d kannst du ganz einfach in die Formel einsetzen:
O = π · d²
O = π · (12 cm)²
O = π · 144 cm²
O ≈ 452,39 cm²
Die Oberfläche beträgt ca. 452,39 cm².
Volumen einer Kugel
Der Rauminhalt einer Kugel wird als Volumen V bezeichnet. Mit folgender Formel kannst du ganz einfach Volumen berechnen:
V = “vier Drittel mal Pi mal Radius hoch 3” = (4/3) · π · r³
oder
V = “ein Sechstel mal Pi mal Durchmesser hoch 3” = (1/6) · π · d³
Auf geht’s! Teste die gelernte Formel in den Übungsaufgaben. Eine Zusammenfassung aller Formeln für Volumen berechnen findest du übrigens hier. Außerdem erfährst du hier, wie du Volumeneinheiten schnell und einfach umrechnest.
Der Radius der Kugel beträgt r = 2,5 dm. Wie groß ist ihr Volumen?
Volumen der Kugel berechnen: Setze den Radius (r = 2,5 dm ) in die Volumenformeln ein:
V = (4/3) · π · r³
V = (4/3) · π · (2,5 dm)³
V = (4/3) · π · 15,625 dm³
V ≈ 65,45 dm³
Das Volumen beträgt ca. 65,45 dm³.
Wie groß ist das Volumen einer Kugel, wenn sie einen Durchmesser von d = 18 cm hat?
Berechne zuerst aus dem Durchmesser (d = 18 cm) den Radius:
r = ½ · 18 cm = 9 cm
Danach setzt du den Radius in die Volumenformel ein:
V = (4/3) · π · r³
V = (4/3) · π · (9 cm)³
V = (4/3) · π · 729 cm³
V ≈ 3053,63 cm³
Das Volumen beträgt ca. 3053,63 cm³.
Kreisfläche einer Kugel
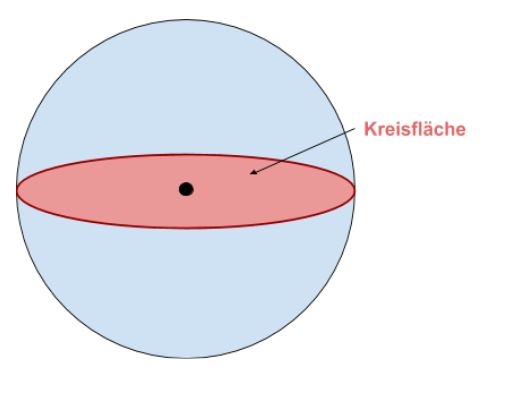
Die Kreisfläche A (manchmal auch Kreisausschnitt genannt) verläuft genau durch den Mittelpunkt der Kugel (siehe Abbildung). Sie halbiert also die Kugel.
Der Durchmesser der Kreisfläche entspricht damit genau dem Durchmesser der Kugel.
A = π · r²
Auch zur Kreisfläche haben wir zwei Aufgaben samt Lösungen für dich. Aber probiere zunächst, die Übungen alleine zu lösen 😉
Ein vollkommen runder Ball hat einen Radius von 3,5 cm. Wie groß ist seine Kreisfläche?
A = π · r²
A = π · (4,5 cm)²
A = π · 20,25 cm²
A ≈ 63,62 cm²
Die Kreisfläche hat eine Größe von ca. 63,62 cm².
Wie groß ist die Kreisfläche, wenn der Durchmesser der Kugel d = 19 cm ist?
A = π · r²
A = π · (9,5 cm)²
A = π · 90,25 cm²
A ≈ 283,53 cm²
Die Kreisfläche hat eine Größe von ca. 283,53 cm².
FAQ
Zum Abschluss haben wir eure wichtigsten Fragen hier noch einmal aufgelistet. Klicke einfach auf das +, um die Antwort zu lesen.
Was ist eine Kugel?
Eine Kugel ist ein perfekt runder geometrischer Körper, bei dem alle Punkte der Oberfläche (= Außenfläche) denselben Abstand zum Mittelpunkt der Kugel haben.
Wie viele Flächen hat eine Kugel?
Eine Kugel hat nur eine Fläche (ihre Außenfläche).
Wie berechnet man den Radius einer Kugel?
Um den Radius auszurechnen, brauchst du lediglich die Formeln, die du bereits kennst. Diese stellst du so um, dass der Radius alleine auf einer Seite steht, z.B:
Durchmesser: d = 2 · r ⇒ r = ½ · d
Oberfläche: O = 4· π · r² ⇒ 
Volumen: V = (4/3)· π · r³ ⇒ 
usw.
Wie berechne ich das Volumen einer Kugel?
Das Volumen einer Kugel berechnest du mit folgender Formel:
Volumen: V = (4/3)· π · r³
Wie berechnet man die Oberfläche einer Kugel?
Die Oberfläche einer Kugel kannst du mit folgenden Formeln berechnen:
O = 4· π · r² oder
O = π · d²
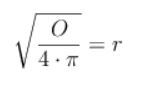
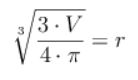
Hat geholfen, danke!
immer cool sich zu erinnern, erinnert zu werden.erinnert zu werden wie klein eine kugel sein kann im großen universum.
danke
Kugel Volumen kann auch 1/6 pi mal d³ sein
Hat mir meinen Vortrag gerettet. Danke !