3,00 von 5 Sterne
Loading...
Einen Bruche multiplizieren ist nicht immer einfach und wird in der Schule oft nur schlecht erklärt.
Hier erfährst du wie es ganz einfach funktioniert, damit du beim nächsten Mathe-Test richtig durchstartest!
Im Folgenden erfährst du…
- …wie man einen Bruch multipliziert,
- …wie man Brüche mit ganzen Zahlen multipliziert,
- …und wie man Brüche mit gemischten Zahlen multipliziert,
…alles mit Beispielen und Aufgaben zum Selbsttest!
Los geht’s!
Um zwei Brüche miteinander zu multiplizieren, gilt folgende Regel:
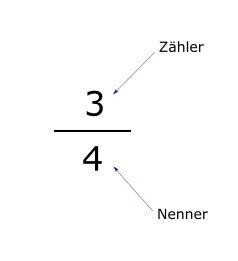
Der Zähler wird mit dem Zähler des anderen Bruchs und der Nenner mit dem Nenner des anderen Bruchs multipliziert.
Was sind Brüche?
Ein Bruch ist immer ein Teil eines Ganzen. Beispiel: Ein Stück Pizza von sechs, entspricht dem mathematischen Bruch von \frac{1}{6}.
Über dem Bruchstrich steht der Zähler, der den Anteil vom Ganzen (hier 1) angibt. Unter dem Bruchstrich steht der Nenner, der das Ganze angibt (hier 6).
Eine Schaubild zum Bruch \frac{3}{4}:
Bruch multiplizieren Beispiel
\frac{1}{3} x \frac{3}{4} = ?
Die beiden Zähler, 1 und 3, werden miteinander multipliziert: 1 x 3 = 3
Die beiden Nenner, 3 und 4, werden miteinander multipliziert: 3 x 4 =12
Der Bruch der als Ergebnis steht ist damit:
\frac{3}{12}
Gekürzt mit dem Faktor 3 ist das Endergebnis:
\frac{1}{4}
Ein weiteres Beispiel:
\frac{2}{5} x \frac{4}{9} = ?
Zähler mal Zähler und Nenner mal Nenner ergibt:
\frac{8}{45}
Ergebnis kürzen nicht vergessen! Ein Bruch, bei dem Zähler und Nenner durch die gleiche Zahl geteilt werden können, ist kürzbar! Beispiele: \frac{3}{6} gekürzt mit dem Faktor 3 ist : \frac{1}{2}. Der Bruch \frac{8}{24} gekürzt mit dem Faktor 8 ist: \frac{1}{3}. Finde immer die größte Zahl, mit der sich sowohl Zähler als auch Nenner teilen lassen!
Bruch multiplizieren mit ganzer Zahl
Ein besonderer Fall der Bruchmultiplikation, auf den du vielleicht schon gestoßen bist, ist die Multiplikation eines Bruchs mit einer ganzen Zahl.
Diese scheint erst verwirrend, denn wie soll man bitte eine Zahl mit einem Bruch zusammenrechnen? Eigentlich ist das aber ganz leicht, wie du gleich sehen wirst:
Zuerst musst du die ganze Zahl in einen Bruch umwandeln. Das machst du, indem du die Zahl als Zähler und 1 als Nenner verwendest.
Gegeben ist die ganze Zahl 6. Der Bruch dieser Zahl würde so aussehen:
\frac{6}{1}
Die Zahl 6 im Zähler drückt aus, dass das Ganze (also die 1 im Nenner) 6 mal vorkommt.
Nun muss man nur noch den Bruch wie gelernt mit dem anderen multiplizieren.
Beispiel:
4 x \frac{2}{3}
ist gleich:
\frac{4}{1} x \frac{2}{3}
Das Ergebnis ist also:
\frac{8}{3}
Bruch multiplizieren mit gemischten Zahlen
Bei einer Rechnung wie:
3 \frac{1}{2} x \frac{2}{5}
spricht man von einer Multiplikation von einem Bruch mit einer gemischten Zahl. Gemischte Zahlen sind eine Mischung aus einer ganzen Zahl und einem Bruch. Bei der Rechnung ist 3 \frac{1}{2} die gemischte Zahl.
Um gemischte Zahlen zu multiplizieren muss die ganze Zahl in den dazugehörigen Bruch integriert werden. Dazu wird wie folgt vorgegangen:
- Die ganze Zahl wird mit der Zahl im Nenner des Bruchs multipliziert
- Das Ergebnis wird dem Zähler aufaddiert
- Der neu entstandene Bruch wird wie gewohnt multipliziert
Ein Beispiel mit der Rechnung:
3 \frac{1}{2} x \frac{2}{5}
3 x 2=6 → Multiplikation der ganzen Zahl (3) mit dem Nenner des Bruchs (2)
Nun werden die Ergebnisse mit den jeweiligen Zählern zusammengerechnet:
6 + 1=7 → Addition des vorigen Ergebnisses (6) muít dem Zähler (1)
Wenn bei 3 \frac{1}{2} die ganze Zahl 3 in den Bruch integriert wird, ist der Bruch demnach: \frac{7}{2}
Die neue Rechnung ist:
\frac{7}{2} x \frac{2}{5}
Das Ergebnis ist:
\frac{14}{10}
Bruch multiplizieren mit gemischten Zahlen Aufgaben
Häufig gestellte Fragen / FAQ
Man multipliziert Zähler und Zähler und Nenner und Nenner miteinander.
Man stellt die ganze Zahl als Bruch dar (ganze Zahl als Zähler und 1 als Nenner) und multipliziert diesen wie gewohnt mit dem anderen Bruch.
Man multipliziert die ganze Zahl der gemischten Zahl mit dem Nenner des Bruchs und addiert das Ergebnis dem Zähler auf. Der Bruch wird nun wie gewohnt mit dem anderen Bruch multipliziert.
Bruch multiplizieren Rechner
Für einen Rechner, der automatisch beliebige Brüche multipliziert, klicke auf diesen Link: https://www.mathepower.com/bruchmal.php
Wenn dir diese Erklärungen geholfen haben, dann lass doch einen Kommentar da. Wenn du Fragen oder Probleme hast, dann kannst du diese natürlich ebenfalls stellen – am besten direkt bei unserem Nachhilfe-Team! Wir sind nicht nur in Berlin, Köln oder München vertreten, sondern deutschlandweit! Und für noch mehr Flexibilität kann man stets auf unser beliebtes Online-Nachhilfe Programm zurückgreifen. Probiere es gerne aus und komme zu einem kostenlosen Kennenlerntermin!
Falls du wissen möchtest wie Brüche addiert oder dividiert werden, klicke einfach auf die jeweiligen Links:
Addition von Brüchen
Division von Brüchen
Dann noch viel Erfolg mit dem nächsten Mathetest oder einfach beim Bearbeiten deiner Hausaufgaben!
