4,50 von 5 Sterne
Loading...
Ein Dreieck berechnen – wie funktioniert das überhaupt? Und was versteht man unter einem gleichschenkligen oder gleichseitigen Dreieck? Wir haben die wichtigsten Infos rund um das Dreieck für dich zusammengefasst und zeigen dir anhand von Beispielen, wie du spielend leicht Umfang und Flächeninhalt berechnest!
Eckpunkte
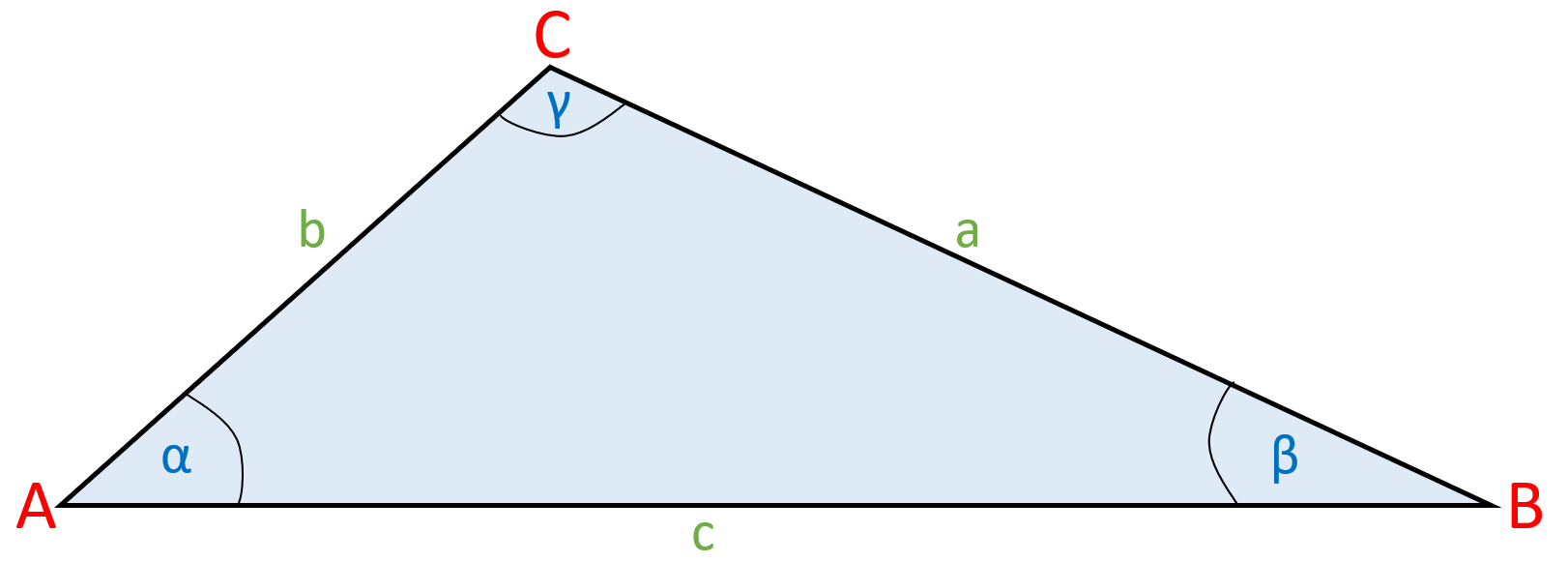
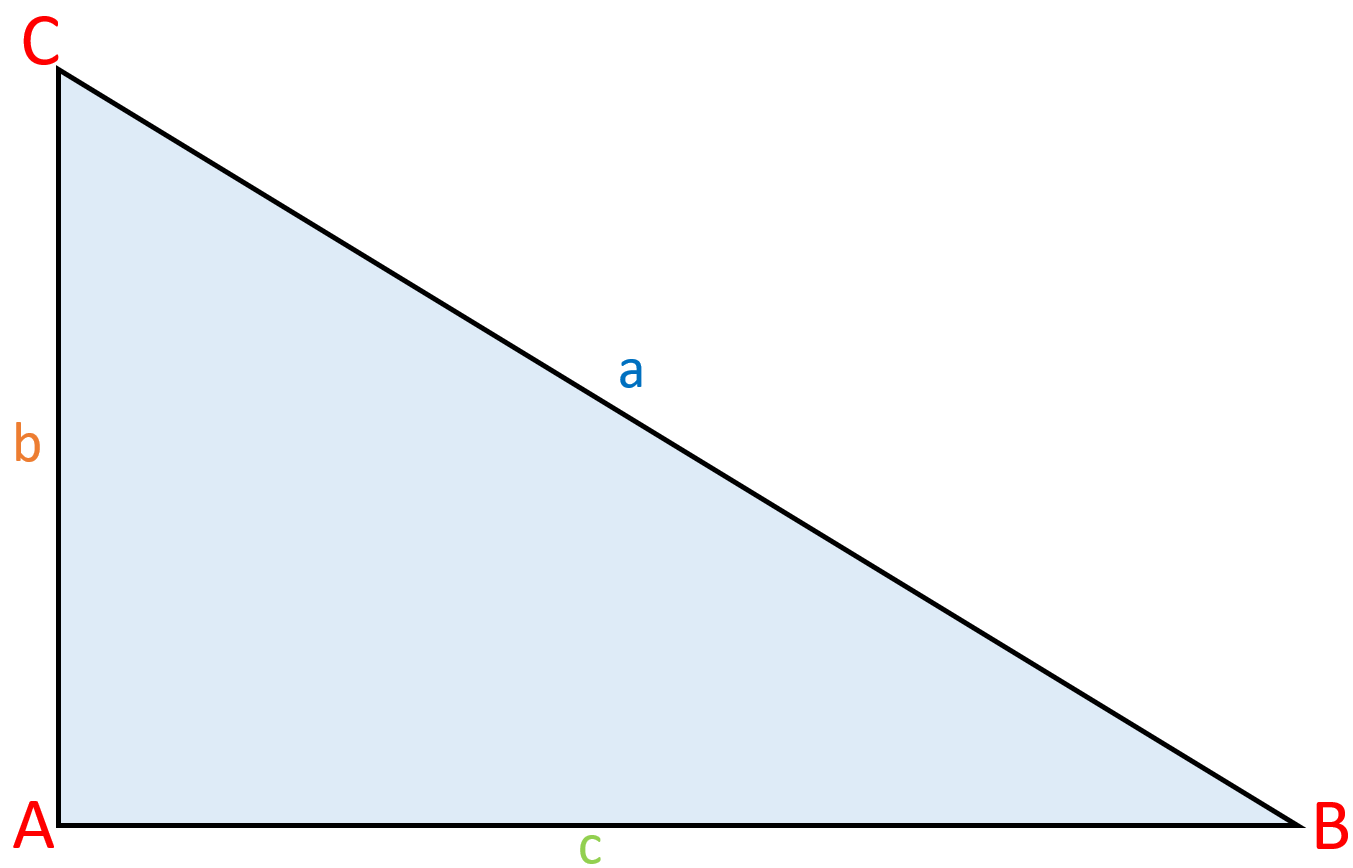
Die drei Eckpunkte eines Dreiecks werden – üblicherweise entgegen des Uhrzeigersinns – mit den Großbuchstaben A, B und C gekennzeichnet.
Seiten
Alle Dreieck-Seiten werden nach ihren gegenüberliegenden Eckpunkten benannt und mit Kleinbuchstaben markiert: a, b und c. So liegt etwa die Seite c dem Punkt C gegenüber.
Innenwinkel
Die Innenwinkel werden mit den griechischen Buchstaben α (Alpha), β (Beta) und γ (Gamma) beschriftet. Alpha ist der Winkel am Eckpunkt A, Beta am Punkt B und Gamma am Punkt C.
Was ist ein rechtwinkliges Dreieck?
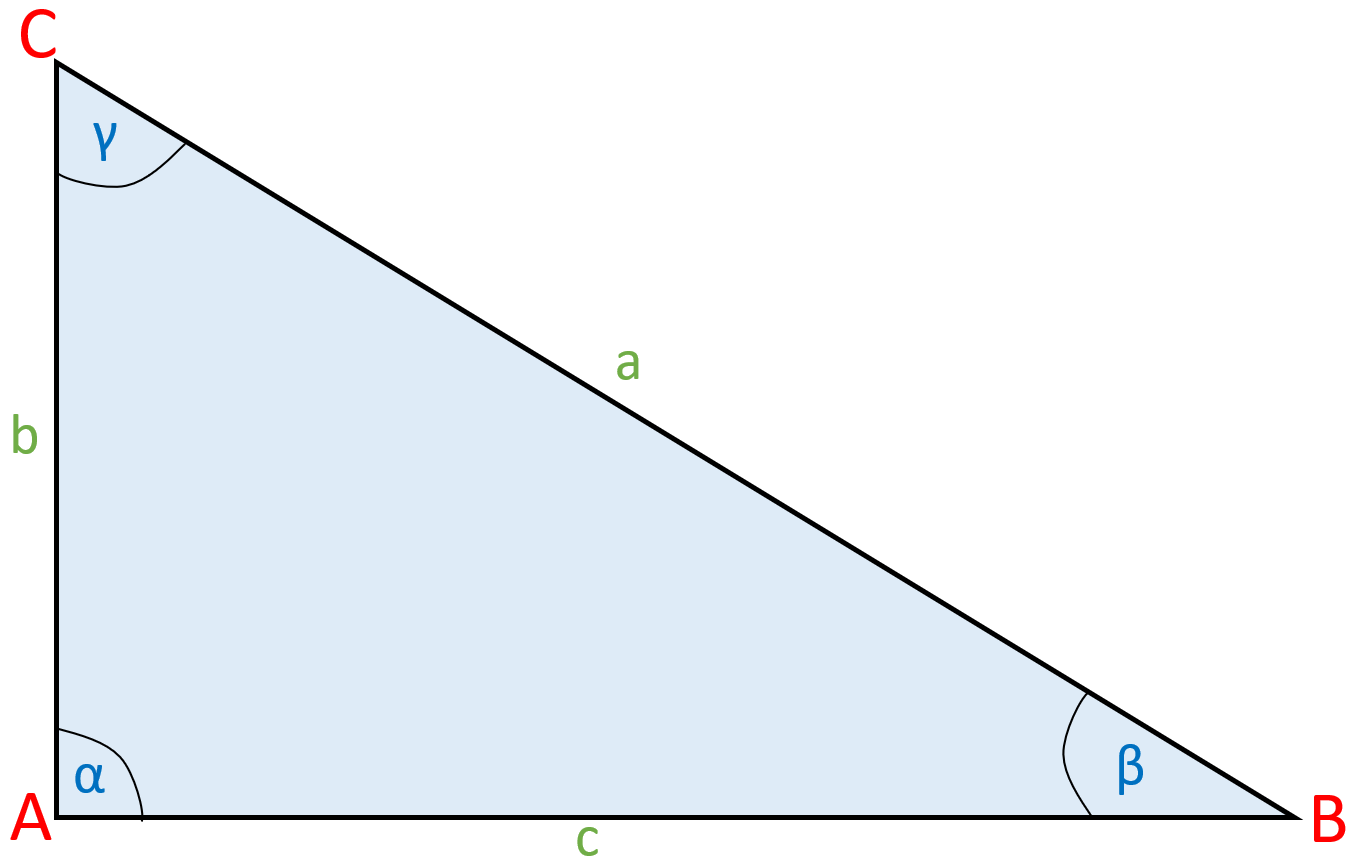
Ein rechtwinkliges Dreieck besitzt einen rechten Winkel, also einen Winkel, der genau 90° groß ist.
Folgendes solltest du zum rechtwinkligen Dreieck wissen:
- Die längste Seite wird Hypotenuse genannt. Sie liegt gegenüber des rechten Winkels.
- Die übrigen Seiten werden als Katheten bezeichnet. Sie sind also die beiden Seiten, die den rechten Winkel bilden.
- Für die Flächenberechnung eines rechtwinkligen Dreiecks wird eine andere Formel als bei anderen Dreiecken verwendet. Mehr dazu erfährst du in den nächsten Abschnitten.
Seitenverhältnis im Dreieck
Die Seitenlängen können in unterschiedlichem Verhältnis zueinander stehen. Daraus lassen sich verschiedene Dreiecks-Arten ableiten.
Ungleichseitiges Dreieck
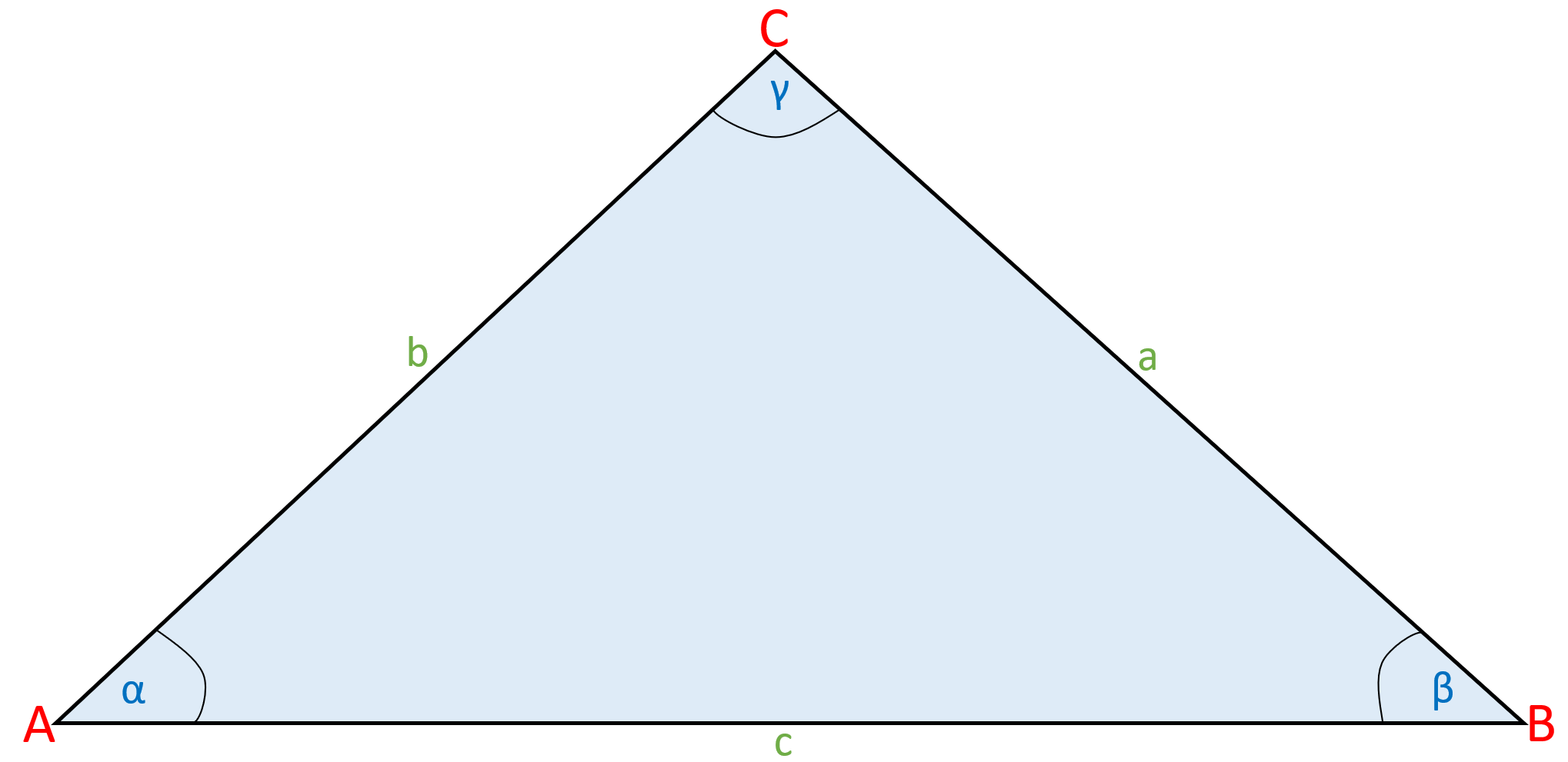
Bei einem ungleichseitigen Dreieck sind alle Seiten unterschiedlich lang. Auch die Innenwinkel sind unterschiedlich groß
Gleichseitiges Dreieck
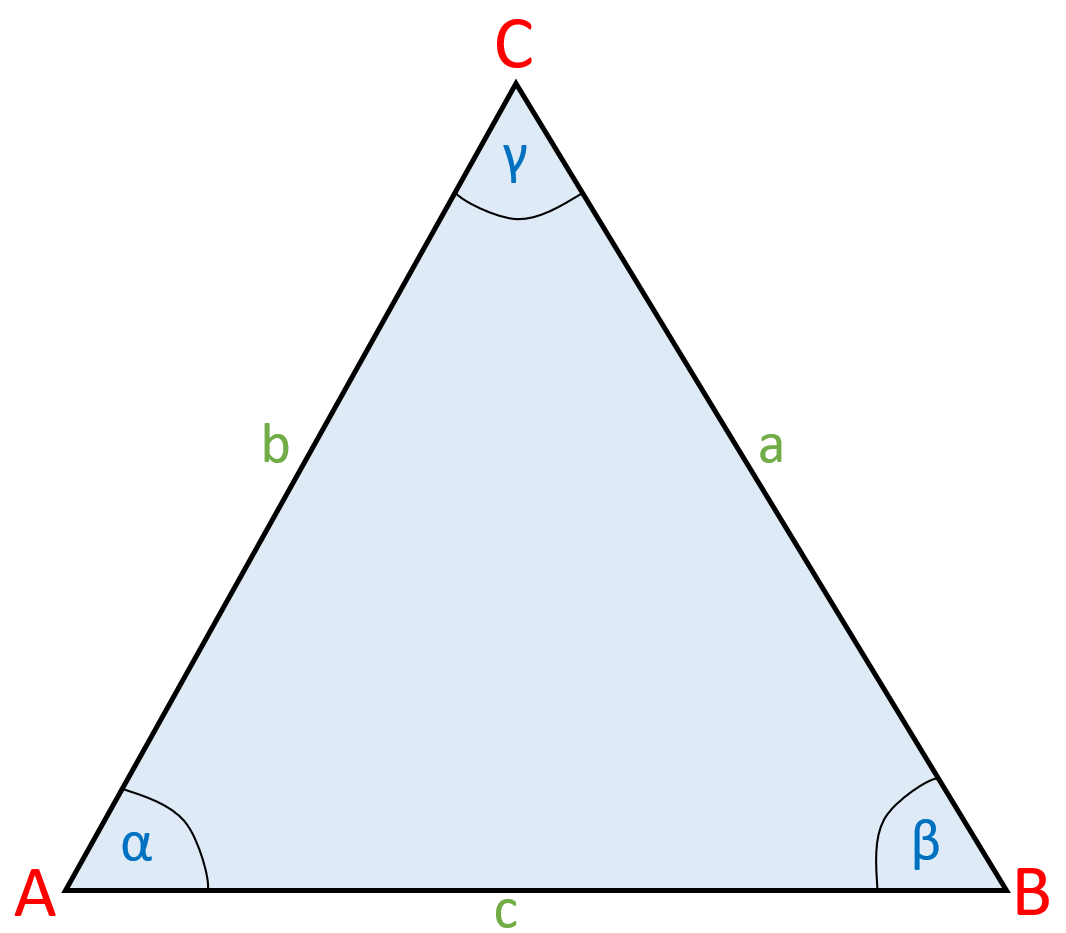
Ein Dreieck, bei dem alle Seiten gleich lang sind, wird gleichseitiges Dreieck genannt. Auch die Innenwinkel sind bei dieser Dreieck-Art gleich groß, sie betragen 60°.
Gleichschenkliges Dreieck
Bei einem gleichschenkligen Dreieck sind zwei Seiten gleich lang. Diese beiden Seiten werden a und b genannt und als Schenkel des Dreiecks bezeichnet. Auch zwei Winkel haben dadurch diesselbe Größe (hier α und β).
Dreieck Formeln – alles was du brauchst!
Umfang Dreieck
Die Berechnung des Umfangs U eines Dreiecks ist ganz simpel und für alle Dreiecksarten gleich. Du addierst hierfür einfach die einzelnen Seitenlängen:
U = Umfang a = Seite a
b = Seite b c = Seite c
Probiere es selbst aus und bearbeite die folgenden Übungsaufgaben! Wenn du nicht weiterkommst, haben wir natürlich auch die Lösung parat.
Berechne den Umfang eines Dreiecks, das die Seitenlängen a = 11 cm, b = 4,5 cm und c = 9 cm hat.
Wir haben die Seitenlängen alle gegeben. Somit können wir sie einfach in die Formel einsetzen:
U = a + b + c
U = 11 cm + 4,5 cm + 9 cm
U =24,5 cm
Der Umfang des Dreiecks beträgt 24,5 cm.
Ein gleichseitiges Dreieck hat die Seitenlänge c = 5 cm. Berechne seinen Umfang!
Wir wissen, dass das Dreieck gleichseitig ist. Das heißt, alle Seiten haben dieselbe Länge:
a = b = c = 5 cm
U = a + b + c
U = 5 cm + 5 m + 5 cm
U = 15 cm
Der Umfang des Dreiecks beträgt 15 cm.
Das Dreieck ist gleichschenklig und hat einen Umfang von 20 cm. Die Seite c ist 5 cm lang. Berechne die Länge der Schenkel a und b!
Da das Dreieck gleichschenklig ist, sind die Seiten bzw. Schenkel a und b gleich lang:
a = b
Daher können wir b in der Formel durch a ersetzen und lösen die Formel nach a auf:
U = a + a + c
20 cm = a + a + 5 cm
20 cm – 5 cm = a + a
15 cm = 2 · a
7,5 cm = a = b
Die Schenkel a und b haben beide eine Länge von 7,5 cm.
Flächeninhalt Dreieck berechnen
Um den Flächeninhalt eines Dreiecks zu berechnen, musst du die Länge der Grundseite mit der Höhe multiplizieren und das Ergebnis durch 2 teilen.
Die Formel hierzu lautet:
A = Flächeninhalt Dreieck
g = Grundseite
h = Höhe der Grundseite
g und h müssen vor der Berechnung in der gleichen Maßeinheit vorliegen!
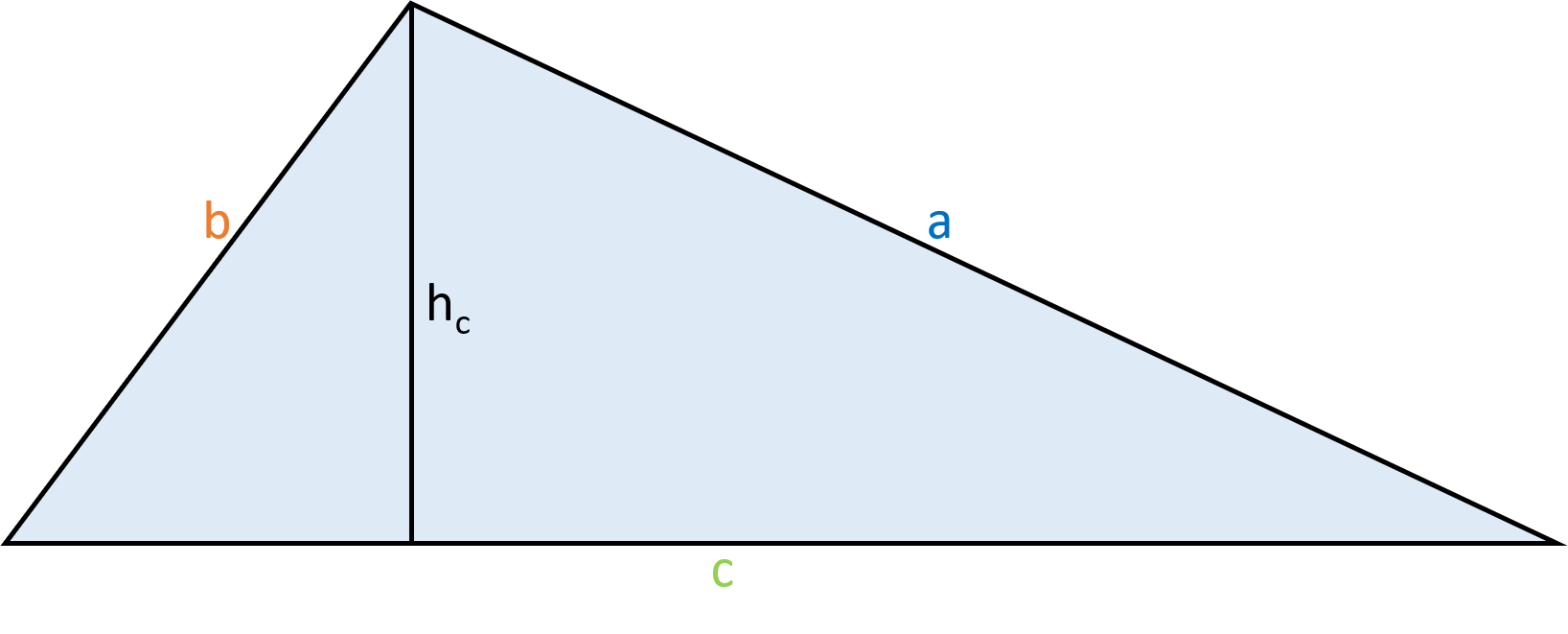
Der Rechenweg wird in den beiden oberen Abbildungen veranschaulicht. Links siehst du ein Dreieck mit den Seitenlängen a, b und c. Außerdem ist die Höhe von c (= hc) eingezeichnet.
Die Höhe einer Seite ist ein Lot, also eine senkrechte Linie, die die Seite mit dem gegenüberliegenden Eckpunkt verbindet. Jede Dreieck-Seite besitzt solch ein Lot.
Klick auf den folgenden Tab, wenn du die Herleitung der Flächenformeln genauer verstehen möchtest.
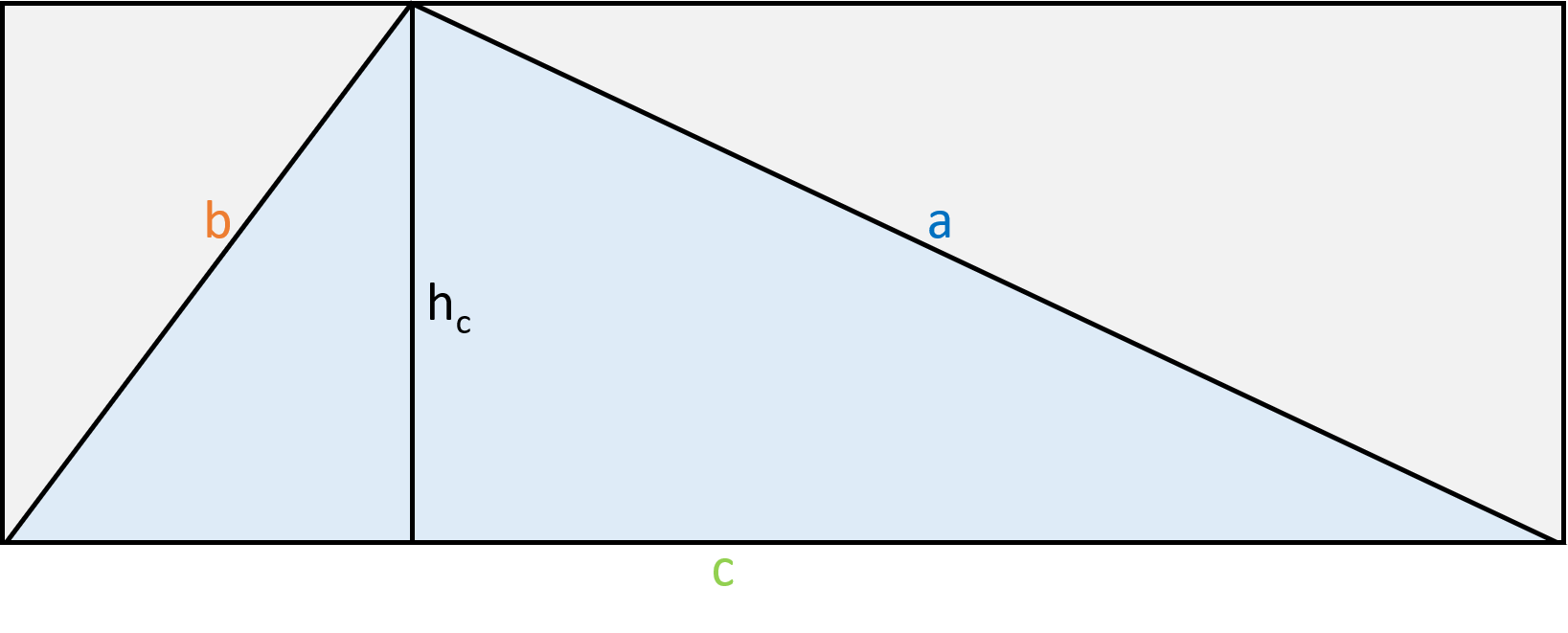
Wie du in den Abbildungen siehst, wird das Dreieck durch das Einzeichnen der Höhe von c in zwei rechtwinklige Dreiecke geteilt. Ergänzt man diese Dreiecke um zwei kongruente (= deckungsgleiche) Dreiecke (Abbildung rechts), erhält man ein Rechteck.
Nun wird klar, dass man die Fläche eines Rechtecks berechnet und dieses Ergebnis durch zwei teilt. Das Rechteck hat in diesem Fall die Seitenlängen c (= Grundfläche) und hc (= Höhe der Grundfläche):
A (Rechteck) = c · hc = g · h
→ daraus folgt: A (Dreieck) = ½ · g · h
A (Rechteck) = Flächeninhalt Rechtecks
A (Dreieck) = Flächeninhalt Dreieck
g = Grundseite
h = Höhe der Grundseite
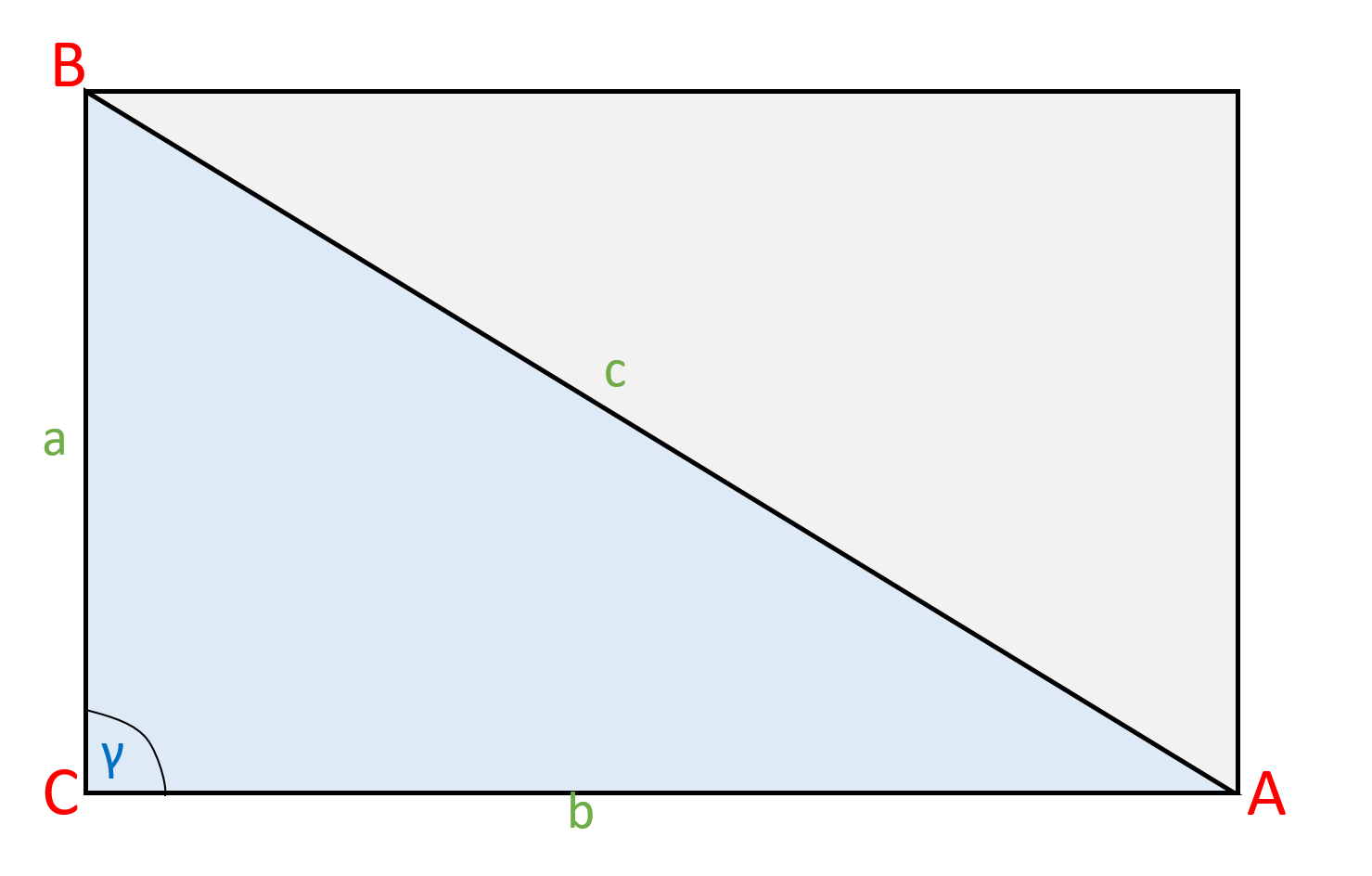
Flächeninhalt rechtwinkliges Dreieck – ein Sonderfall
Noch einfacher ist die Flächenberechnung bei einem rechtwinkligen Dreieck.
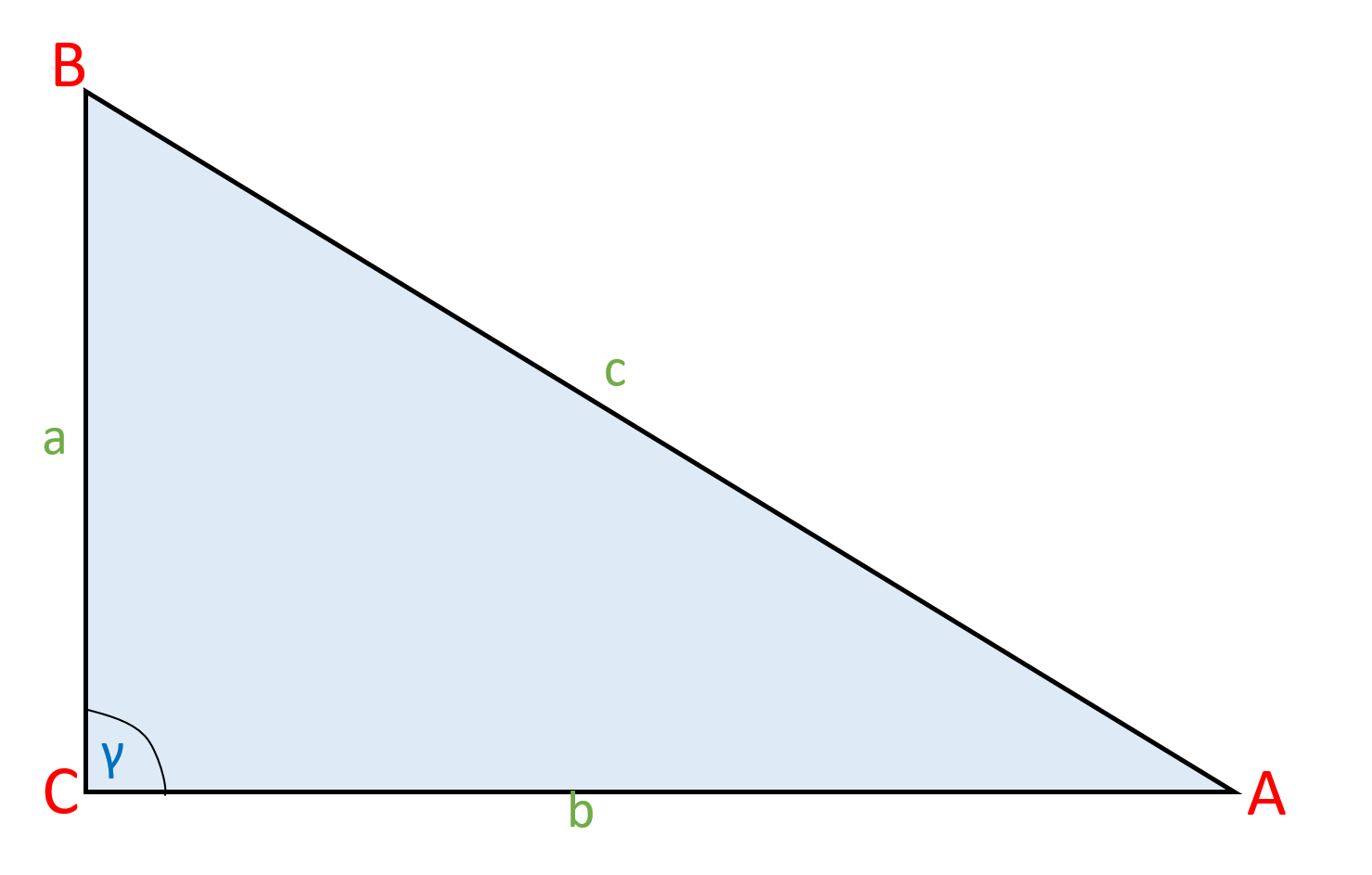
Links siehst du ein Dreieck, dessen Winkel γ = 90 ° ist.
Wie du merkst, kann man das Dreieck verdoppeln, wodurch ein Rechteck entsteht (siehe rechte Abbildung).
Um den Flächeninhalt des Dreiecks zu berechnen, brauchst du also einfach den Flächeninhalt des Rechtecks durch 2 zu teilen:
A = Flächeninhalt Dreieck
a = Seite a
b = Seite b
a und b stehen für die beiden Seiten des Dreiecks, die den rechten Winkel bilden
Flächeninhalt Dreieck berechnen
Schauen wir uns den Rechenweg an einem Beispiel an.
Nun bist du an der Reihe! Wende die Flächenformeln in den folgenden Übungsaufgaben an.
Die Seite a eines Dreiecks besitzt eine Länge von 7 cm. Die Seitenhöhe von a (= ha) beträgt 3 cm. Berechne den Flächeninhalt des Dreiecks.
In diesem Beispiel nehmen wir zur Berechnung die Seite a als Grundseite g. Wir setzen die Werte in die Flächenformel ein:
A = ½ · g · h
A = ½ · 7 cm · 3 cm
A = ½ · 21 cm²
A = 10,5 cm²
Das Dreieck hat einen Flächeninhalt von 10,5 cm².
Du hast ein Dreieck vorliegen, das die Seitenlängen a = 5 cm, b = 10 cm und c = 7 cm hat. Zusätzlich ist die Seitenhöhe von b bekannt, sie beträgt 3 cm. Berechne die Fläche des Dreiecks.
Zwar haben wir alle Seitenlängen gegeben, wir brauchen aber nur die Länge der Grundseite zur Berechnung. Da wir die Seitenhöhe von b kennen, nehmen wir Seite b als Grundseite.
A = ½ · g · h
A = ½ · 10 cm · 3 cm
A = ½ · 30 cm²
A = 15 cm²
Das Dreieck besitzt einen Flächeninhalt von 15 cm².
Die beiden Katheten eines rechtwinkligen Dreieck haben die Seitenlängen a = 15 mm und b = 4 cm. Berechne die Fläche des Dreiecks.
Die beiden Katheten bilden bei einem rechtwinkligen Dreieck den rechten Winkel. Somit haben wir alle Werte, die wir für die Berechnung des Flächeninhalts benötigen.
Achtung: Da die Maßeinheiten bei beiden Seiten unterschiedlich sind, rechnen wir zunächst die Länge von Seite a von Millimeter in Zentimeter um. Wir verwenden die Flächenformel für rechtwinklige Dreiecke:
a = 15 mm = 1,5 cm
b = 4 cm
A = ½ · a · b
A = ½ · 1,5 cm · 4 cm
A = ½ · 6 cm²
A = 3 cm²
Die Fläche des Dreiecks ist 3 cm² groß.
Formel umstellen
Natürlich kannst du die Flächenformeln auch umstellen, um z.B. eine Seitenhöhe oder eine Seitenlänge auszurechnen.
→ g = (A · 2) / h
→ h = (A · 2) / g
Für rechtwinklige Dreiecke:
→ a = (A · 2) / b
→ b = (A · 2) / a
Dreieck berechnen – FAQ
Das Wichtigste in Kürze: Eure meistgestellten Fragen habe wir hier zusammengetragen. Klick einfach auf das +, um die Antwort zu sehen.
Wie viel Grad hat ein Dreieck?
Die Summe der Innenwinkel beträgt bei jedem Dreieck 180°.
Was ist ein gleichschenkliges Dreieck?
Bei einem gleichschenkligen Dreieck sind zwei Seiten gleich lang. Diese beiden Seiten werden als Schenkel bezeichnet.
Was ist ein gleichseitiges Dreieck?
Bei einem gleichseitigen Dreieck sind alle Seiten gleich lang (a = b = c). Dementsprechend sind auch alle Innenwinkel gleich groß, sie betragen allesamt 60° (α = β = γ = 60°)
Was ist ein rechtwinkliges Dreieck?
Ein rechtwinkliges Dreieck besitzt einen rechten Winkel, der also genau 90° groß ist.
Wie berechnet man ein Dreieck?
Für die Berechnung des Umfangs eines Dreiecks benötigst du die drei Seitenlängen. Die Formel lautet:
U = a + b + b
Den Flächeninhalt eines Dreiecks berechnest du mit einer Grundseite (g) und der dazugehörigen Höhe (h):
A = ½ · g · h
Für den Flächeninhalt eines rechtwinkligen Dreiecks gilt eine gesonderte Formel:
A = ½ · a · b
(a und b = die Seiten, die den rechten Winkel bilden)
Wir hoffen diese Übersicht über das Thema konnte dir weiterhelfen. Falls noch Fragen oder Unklarheiten aufgekommen sein sollten, schreib gerne einen Kommentar und lass es uns wissen!
4,50 von 5 SterneLoading...
Vielen Dank, aber könntet ihr auch noch ein paar Informationen zu Dezimahlzahlen zum berechnen einstellen, danke.
moin,
kleiner Schreibfehler bei eurer Dreiecksberechnung.
https://www.nachhilfe-team.net/lernen-leicht-gemacht/dreieck-berechnen/
In der folgenden Box haben wir für dich die grundlegenden Formeln zur Kreisberechnung noch einmal zusammengefasst.
und nun kommen die Formeln für das Dreieck!
Mit freundlichem Gruß
Vielen Dank, wurde korrigiert