5,00 von 5 Sterne
Loading...
Bist du dir nicht sicher wie man Brüche mit ganzen Zahlen addiert oder weißt nicht wie Brüche ohne gemeinsamen Nenner addiert werden?
Das alles und mehr kannst du hier mit ganz simplen Erklärungen und Beispielen lernen! Dein neu gewonnenes Wissen kannst du dann gleich an den Übungsaufgaben anwenden.
Lass uns direkt loslegen!
Ein Bruch ist immer ein Teil eines Ganzen.
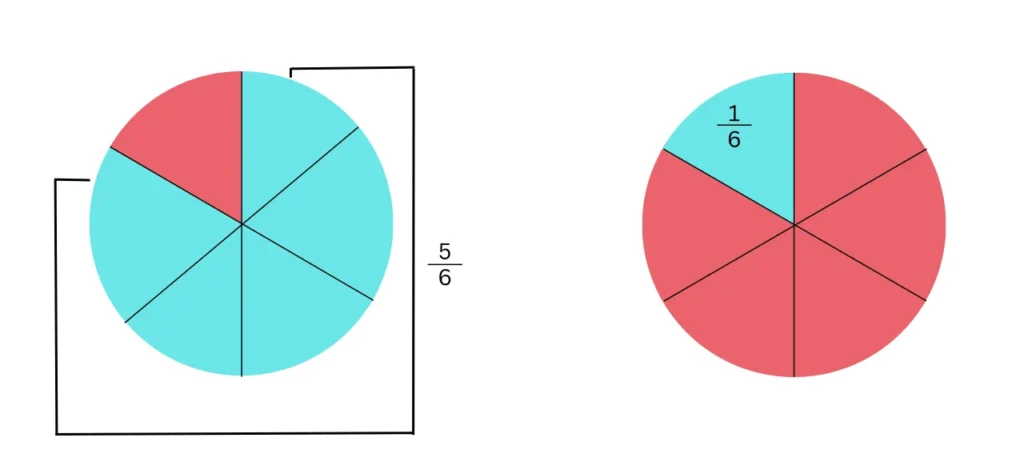
Zum Beispiel hat ein Kuchen 6 Stücke. Damit bilden alle 6 Stücke den ganzen Kuchen. Wenn du 1 Stück davon nimmt bleiben dem Kuchen nur noch 5 der 6 Stücke. Dieser Anteil des Ganzen wird in der Mathematik mit einem Bruch dargestellt:
\frac{5}{6}
Das eine Stück, das du weggenommen hast ist demnach \frac{1}{6} .
Wenn du das Stück wieder zurück legst sind wieder alle 6 Stücke des Kuchens vorhanden, der Bruch dazu ist \frac{6}{6} , also der ganze Kuchen.
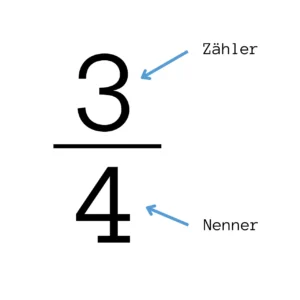
Wie du vielleicht schon gemerkt hast, steht die Zahl der Kuchenstücke des ganzen Kuchens, also 6, unter dem Bruchstrich. Diese Zahl wird Nenner genannt.
Die Zahl über dem Bruchstrich, die den Anteil vom Kuchen angibt, wird Zähler genannt.
Brüche addieren mit gemeinsamen Nenner
In dem Kuchenbeispiel gab es bereits eine Bruchaddition: Das Kuchenstück (eins von sechs, also \frac{1}{6}) das du zum Kuchen zurückgelegt hast, wird zu den 5 vorhandenen Kuchenstücken (also \frac{5}{6}) zusammengezählt. Dies ergibt wieder die 6 Stücke, also den gesamten Kuchen \frac{6}{6}. In der Bruchrechnung sieht das so aus:
\frac{1}{6} + \frac{5}{6} = \frac{6}{6}
Büche addieren mathematisch ausgedrückt: Die Zähler der beiden zu addierenden Brüche werden addiert (1 + 5). Der Nenner bleibt gleich.
Hinweis: Der Zähler kann auch größer als der Nenner sein!
1. \frac{1}{4} + \frac{2}{4} = ?
2. \frac{3}{5} + \frac{2}{5} = ?
3. \frac{4}{7} + \frac{4}{7} = ?
a)
1. \frac{3}{4}
2. \frac{5}{5} = 1
3. \frac{8}{7}
Brüche addieren ohne gemeinsamen Nenner
In dem Kuchenbeispiel und den Beispielaufgaben hatten alle Brüche einen gemeinsamen Nenner. Doch was wenn der Nenner von zwei Brüchen unterschiedlich ist? Ungleichnamige Brüche addieren ist etwas komplizierter, als einfach nur die Zähler zu addieren.
In diesem Fall muss zwischen den Nennern der beiden Brüche ein kleinstes gemeinsames Vielfaches (kgV) gefunden werden.
Angenommen die Rechnung ist:
\frac{1}{2} + \frac{1}{3}
Das kleinste gemeinsame Vielfache der beiden Nenner 2 und 3 ist 6. Nun muss so vorgegangen werden:
Der Zähler vom Bruch links (1) wird mit dem Nenner vom Bruch rechts (3) multipliziert:
1 x 3= 3.
Der Zähler vom Bruch rechts (1) wird mit dem Nenner vom Bruch links (2) multipliziert:
1 x 2 = 2.
Das kgV (6) ist der neue Nenner der beiden Brüche. Die zu addierenden Brüche sehen nun wie folgt aus:
\frac{3}{6} + \frac{2}{6}
Nun da die Brüche wieder einen gemeinsamen Nenner besitzen kann wie gewohnt einfach der Zähler addiert werden:
\frac{3}{6} + \frac{2}{6} = \frac{5}{6}
Ein Sonderfall:
Gegeben ist die Rechnung:
\frac{2}{3} + \frac{1}{6}
Hier ist das kgV 6. Der Bruch links muss also mal 2 multipliziert werden, während der Bruch rechts mal 1 multipliziert wird, also gleich bleibt. Die neue Rechnung ist:
\frac{4}{6} + \frac{1}{6} = \frac{5}{6}
1. \frac{3}{4} + \frac{1}{3} = ?
2. \frac{4}{7} + \frac{3}{5} = ?
3. \frac{3}{8} + \frac{1}{2} = ?
b)
1. kgV ist 12: \frac{9}{12} + \frac{4}{12} = \frac{13}{12}
2. Das kgV ist 35: \frac{20}{35} + \frac{21}{35} = \frac{41}{35}
3. kgV ist 8: \frac{3}{8} + \frac{4}{8} = \frac{7}{8}
Brüche addieren mit ganzen Zahlen
Einen Bruch mit einer ganzen Zahl zu addieren geht einfacher als gedacht!
Dazu muss einfach der Bruch zur ganzen Zahl hinzugefügt werden. Für das Kuchenbeispiel würde das so aussehen: Wenn man 1 Stück eines Kuchens ( \frac{1}{6} ) zu einem ganzen Kuchen, (1) hinzufügen will, dann erhält man 1 \frac{1}{6} Kuchen.
1. \frac{3}{5} + 12 = ?
2. \frac{2}{8} + 4 = ?
3. \frac{12}{6} + 6 = ?
1. 12 \frac{3}{5}
2. 4 \frac{2}{8} = 4 \frac{1}{4}
3. 6 \frac{12}{6} = 6 \frac{2}{1} = 6 +2 = 8
Häufig gestellte Fragen / FAQ
Man addiert die Zähler der Brüche, während der Nenner gleich bleibt.
Zuerst multipliziert man den Zähler des ersten Bruchs mit dem Nenner des zweiten und den Zähler des zweiten Bruchs mit dem Nenner des ersten. Dann multipliziert man die beiden Nenner miteinander, damit dieser gemeinsam ist. Die zwei neuen Brüche werden wie gewohnt addiert, indem die Zähler zusammengerechnet werden.
Man fügt den Bruch ganz einfach zur ganzen Zahl hinzu.
Hoffentlich konnten dir diese Erklärungen weiterhelfen, sodass du im Matheunterricht oder bei der nächsten Klassenarbeit so richtig durchstarten kannst!
Mehr Hilfe gibt es außerdem bei unserer Mathe Nachhilfe. Egal ob direkt vor Ort oder doch Online – unser Nachhilfe-Team hat für jeden das richtige Programm und die besten Tutoren!
Falls du wissen möchtest, wie man Brüche subtrahiert, dividiert oder multiplizierst, dann klick einfach auf die blau markierten Wörter!
Für einen Bruchrechner kannst du auf den folgenden Link klicken: Brüche addieren Rechner
Wenn du noch Fragen oder Probleme hast, kannst du diese in die Kommentare schreiben! Feedback ist immer willkommen!
Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung hinterlässt. Falls du Anmerkungen oder Fragen hast, lass es und doch sehr gerne in den Kommentaren wissen 🙂
5,00 von 5 SterneLoading...