4,57 von 5 Sterne
Loading...
Mit diesem Artikel möchte ich dir einen Überblick über die Matrizen verschaffen. Dafür habe ich ein paar Themen zurecht gelegt, die ich dir mithilfe von Beispielen ein bisschen näher bringen möchte.
Wir werden hier besprechen:
… was Matrizen sind und welche Arten es gibt,
… wie Rechenoperationen durchgeführt werden,
… wie die Determinante und die Inverse berechnet wird und
… die Matrizengleichungen.
Also schau dir doch alles mal in Ruhe an.
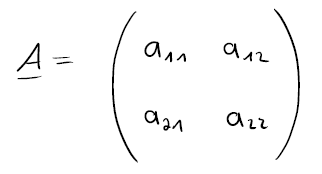
Eine Matrix stellt einen Sachverhalt mittels Zahlenangaben dar und wird auf folgende Art und Weise aufgestellt:
Die Matrix A ist vom Typ (m,n), wobei das m die Zeilenzahl angibt und das n die Spaltenzahl (hier wäre es also (2,2)).
Sie besitzt das Element aij — das a steht für eine Zahl, das i steht für die Zeilenzahl und das j für die Spaltenzahl.
Welche Arten von Matrizen gibt es?
In diesem Abschnitt werde ich dir alle Arten von Matrizen genauer erklären. Also klick einfach mal alles durch, um einen groben Überblick zu bekommen.
Zur Info für dich, bevor wir los legen:
Hauptdiagonale verläuft von links oben bis rechts unten.
Nebendiagonale von rechts oben bis links unten.
Der Spaltenvektor ist eine Matrix mit einer Spalte, also vom Typ (m,1). Dieser Vektor wird meist durch kleine Buchstaben gekennzeichnet.
Ein Zeilenvektor ist eine Matrix mit nur einer Zeile, also vom Typ (1,n). Dieser Vektor wird oftmals gekennzeichnet durch die transponierte Form eines Spaltenvektors.
Bei dieser Art sind alle Elemente gleich Null (ein Vektor dieser Art wird Nullvektor genannt).
Hierbei sind alle Elemente gleich Null, außer die der Hauptdiagonale.
Sie ist eine Diagonalmatrix, bei der alle Elemente auf der Hauptdiagonale gleich 1 sind. Diese Art wird uns im Laufe des Artikels nochmal über den Weg laufen.
Sie ist vom Typ (n,n), was bedeutet, dass sie die gleiche Zeilen- wie Spaltenanzahl besitzt.
Die symmetrische Matrix ist immer gleich ihrer transponierten Matrix.
Die untere Dreiecksmatrix ist quadratisch und alle Elemente oberhalb der Hauptdiagonale sind gleich Null.
Die obere Dreiecksmatrix ist ebenfalls quadratisch und alle Elemente unterhalb der Hauptdiagonale sind gleich Null.
Rechenoperationen mit Matrizen
In diesem Abschnitt werde ich dir die möglichen Rechenoperationen (Addition und Subtraktion, transponieren und die Multiplikation) anhand eines kleinen Beispiels erklären.
Fangen wir doch gleich mal an!
Addition und Subtraktion
Ich habe dir hierzu mal ein kleines Beispiel mitgebracht, damit du sehen kannst, wie das Ganze grundlegend ablaufen würde.
Gegeben sind die folgenden Matrizen:
Die Addition der beiden würde also folgendermaßen aussehen:
Bei der Subtraktion wäre es dann so:
Ansonsten gibt es hierbei nichts großartiges zu beachten.
Transponieren
Hier einmal ein kurzes Beispiel dazu:
Multiplikation
Diesen Abschnitt werde ich in drei Unterabschnitte gliedern:
- eine reelle Zahl mit einer Matrix multiplizieren
- das Skalarprodukt von zwei Vektoren berechnen und
- Matrizen miteinander multiplizieren
Also schau dir alles mal ganz in Ruhe an.
Matrizen mit reeller Zahl
Das grundlegende Berechnungsschema sieht so aus:
Machen wir das Ganze mal an einem Beispiel.
Die Matrix soll mit der Zahl 2 multipliziert werden.
Skalarprodukt von zwei Vektoren
Das grundlegende Berechnungsschema sieht hier folgendermaßen aus:
Nun wenden wir das an einem Beispiel an:
Und das war es auch schon!
Matrizen miteinander multiplizieren
Wir haben einen Artikel über Matrizenmultiplikation vorbereitet, indem alles Schritt-für-Schritt nochmal erklärt wird, falls du Hilfe brauchen solltest.
Dann lass uns gleich anfangen!
Wenn du Matrizen miteinander multiplizieren möchtest, kannst du beispielsweise das Falk-Schema anwenden.
Ich werde dir das hier anhand eines kleinen Beispiels zeigen.
Gegeben sind:
Zuerst prüfen wir die Voraussetzung, ob die beiden überhaupt miteinander multipliziert werden können: Die Matrix A ist vom Typ (2,2) und die Matrix B vom Typ (2,3), unsere Voraussetzung ist also erfüllt.
Nun ordnen wir sie nach dem Falk-Schema folgendermaßen an:
Ganz wichtig hierzu!
Bei der Multiplikation von Matrizen gilt KEIN Kommutativgesetz!
Das bedeutet, dass du die Reihenfolge der Faktoren auf keinen Fall ändern darfst, da sonst ein anderes Endergebnis rauskommt.
Das grundlegende Schema zur Berechnung sieht folgendermaßen aus:
Wenden wir das nun an unserem Beispiel an:
Ergibt das folgende Matrix:
Das ist es auch schon gewesen!
Also lass dir Zeit und rechne es zur Not nochmal nach.
Inverse Matrix
Dieser Abschnitt ist in zwei Teile unterteilt:
- einmal die Determinanten und deren Berechnung und
- als Zweites die Berechnung der Inversen.
Da die Determinanten als Voraussetzung für die Inverse berechnet werden müssen, erkläre ich dir hier gleich alles zusammen.
Aber, bevor es los geht!
Wir haben einen eigenen Artikel über inverse Matrizen verfasst.
Hier findest du eine Schritt-für-Schritt Anleitung zur Berechnung der Determinanten und Inversen (bei 2×2 und 3×3 Matrizen).
Also schau gerne mal vorbei, falls du ausführliche Rechenbeispiele brauchst.
Determinanten
Starten wir gleich mal mit den Determinanten!
Die Berechnung verläuft auf unterschiedliche Art und Weise – je nach dem, welchen Wert das n besitzt.
Ich werde dir hier anhand eines Beispiels zeigen, wie die Berechnung bei einer 2×2 Matrix aussehen würde.
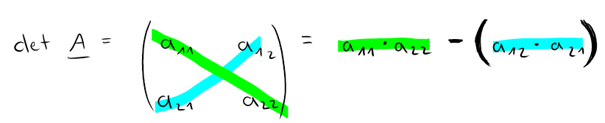
Wir beginnen wieder mit dem grundlegenden Schema:
Jetzt wenden wir das mal an einem Beispiel an:
Perfekt, das ist es schon gewesen!
Zum Thema (oder Auffrischen) siehe auch: Kreuzprodukt, Extremwertaufgabe, & pq-Formel
Ist die Determinante berechnen worden, kann es weitergehen mit der inversen Matrix, denn:
Nur wenn die Determinante ungleich Null ist, besitzt die Matrix auch eine Inverse. Somit muss dies immer als Voraussetzung geprüft werden, bevor es an die inversen Matrizen geht.
Also machen wir doch gleich mal an der Stelle weiter.
Inverse berechnen
Sie wird beispielsweise gebraucht für die Berechnung einer Gleichung mit Matrizen, was wir im nächsten Abschnitt genauer durchgehen werden.
Aber zuerst werde ich dir die Berechnung der inversen Matrix anhand eines Beispiels zeigen.
Der erste Schritt ist, die Determinante der Matrix A zu berechnen:
Als zweiten Schritt ist nun die Voraussetzung für eine Inverse zu prüfen:
Wie du bei unserer Berechnung sehen kannst, ist die Determinante -1. Da sie ungleich Null ist, ist die Matrix regulär und besitzt eine Inverse.
Die Inverse werden wir nun im dritten Schritt zusammen berechnen.
Wie gewohnt starten wir wieder mit dem grundlegenden Berechnungsschema:
Ganz wichtig hierzu!
Die Faktoren a und d tauschen ihre Position. Bei b und c wird ein Minus vorgesetzt!
Wenn wir das an unserem Beispiel anwenden, sieht das folgendermaßen aus:
Die Inverse unserer Ausgangsmatrix lautet also:
Und das war es auch schon mit der Inversen. Bei 2×2 Matrizen ist die Berechnung sehr übersichtlich und recht simpel.
Die 3×3 Matrizen sehen da schon anders aus. Wenn du dir das Verfahren dazu mal anschauen willst, schau mal bei unserem Artikel über die Inverse vorbei.
Lass uns jetzt mit dem letzten Abschnitt weiter machen, den Matrizengleichungen.
Matrizengleichungen
Es soll eine Gleichung aufgelöst werden (bspw. nach X), aber das geht nicht ganz nach dem Verfahren, wie wir es bisher kennengelernt haben. Deshalb müssen wir etwas kreativer werden.
Bevor wir mit einem Beispiel anfangen, erstmal etwas ganz wichtiges:
Beim Multiplizieren von Matrizen gilt kein Kommutativgesetz – die Reihenfolge der Faktoren darf nicht vertauscht werden!
Wirf mal einen Blick auf bestimmte Gesetzmäßigkeiten, die für die Berechnung wichtig werden.
Ich habe dir hier eine Übersicht mitgebracht:
Und einmal zur Multiplikation.
Hierbei sind gerade die letzten beiden besonders wichtig zu beachten, weil sich NUR DA die Position der Faktoren vertauscht.
So, lass uns dann mal mit einem Beispiel anfangen. Ich werde dir alles Schritt-für-Schritt einmal erklären, damit du das grundlegende Verfahren mal kennenlernst.
Gegeben ist die folgende Gleichung, die wir nach X auflösen wollen:
(alle vorkommenden Matrizen sind vom Typ (n,n) und regulär.)
Der erste Schritt: Klammer auflösen, falls vorhanden
In unserem Beispiel würde das folgendermaßen ablaufen (wichtig: beachte die Gesetze)
Der zweite Schritt wäre, Terme zusammenzufassen und zu sortieren.
Das ist hier allerdings nicht möglich, deshalb springen wir gleich weiter zum nächsten Schritt
Der dritte Schritt ist, nach der gesuchten Matrix auszuklammern.
Achtung: behalte die Position im Auge – die Matrix X steht als Faktor rechts. Deshalb muss sie beim Ausklammern auch auf der rechten Seite stehen.
Info: Das X wird zur 1 (das kennen wir ja auch schon). Bei Matrizengleichungen steht dann keine 1 dort, sondern die Einheitsmatrix E.
Der vierte Schritt ist nun, die entstandene Klammer auf die andere Seite zu bringen.
Das wird durch die Inverse erreicht, was folgendermaßen aussehen würde:
Hier wieder aufpassen: die entstandene Klammer bleibt links, weil sie zuvor als Faktor ebenfalls links stand!
Der letzte Schritt ist nun, das Ergebnis zu berechnen bzw. abzulesen
Und das war es auch schon!
Das ganze Thema brauch schon ein bisschen Einarbeitung, weshalb du die Schritte immer mal durchgehen solltest.
Zusammenfassung über Matrizen
Du hast in diesem Artikel gelernt,
wie Rechenoperationen mit Matrizen und Vektoren durchgeführt werden, wie man die Determinante und die Inverse einer Matrix berechnen kann und wie Matrizengleichungen gelöst werden können.
Alles in allem ist auf den ersten Blick etwas kompliziert, aber wenn du die Schemata lernst und Aufgaben übst, dann wirst du darin keine Probleme mehr haben!
Konnte dir der Artikel helfen?
Wir haben uns viel Mühe bei der Erstellung des Artikels gegeben.
Deshalb würden wir uns sehr darüber freuen, wenn du uns mitteilst, ob und wie der Artikel dir weiterhelfen konnte.
Vielen Dank!
4,57 von 5 SterneLoading...
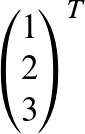
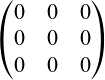
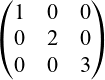
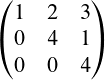
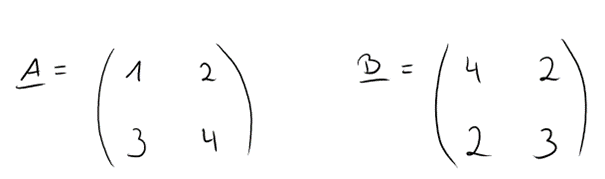
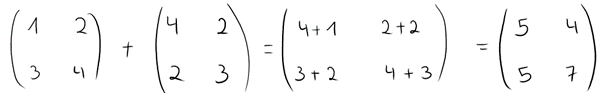
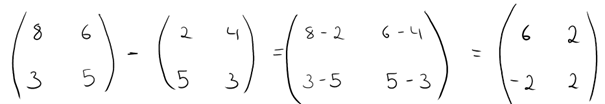
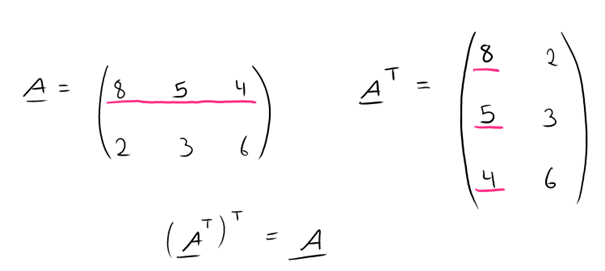
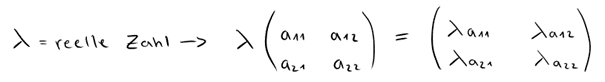
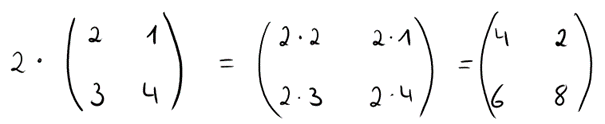
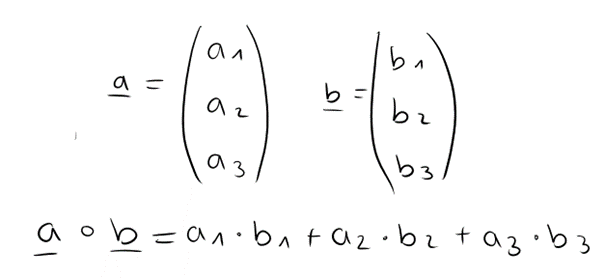
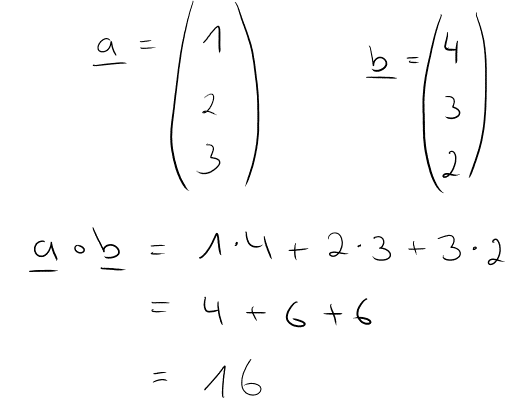
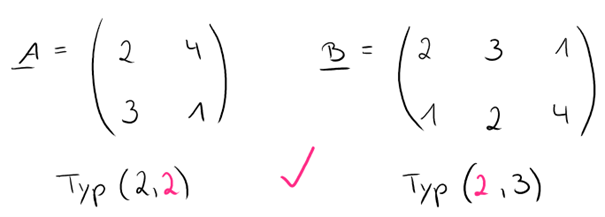
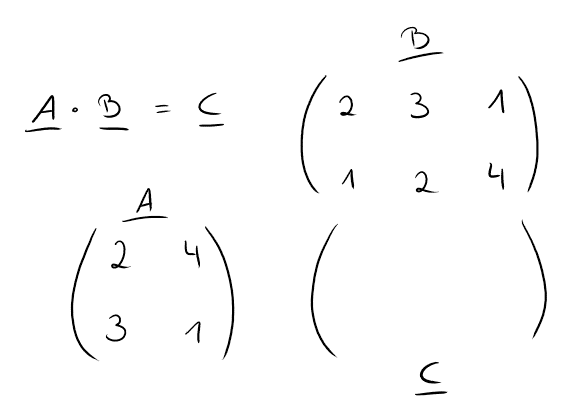
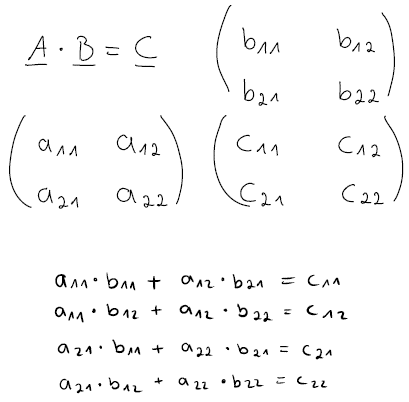
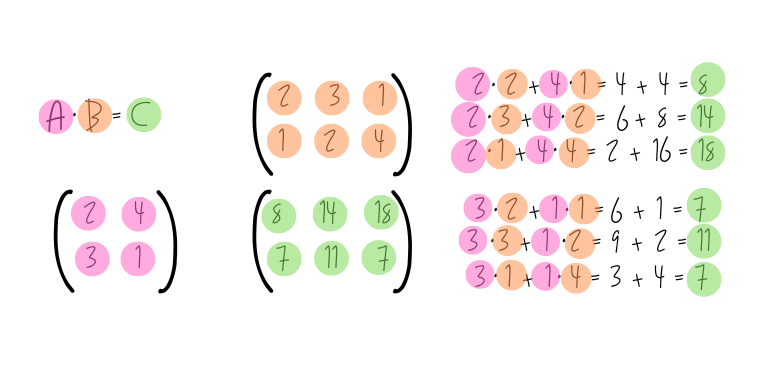
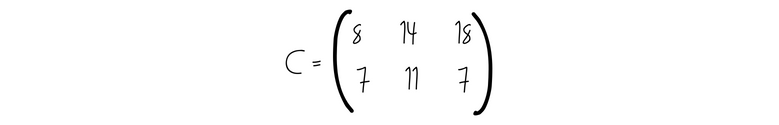
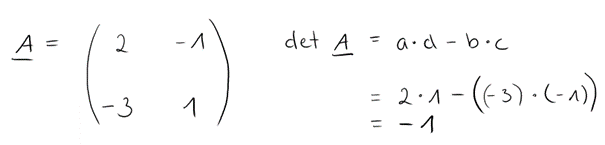
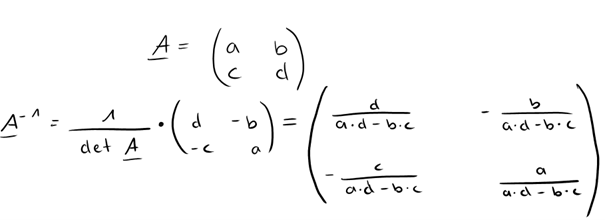
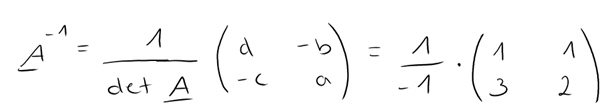
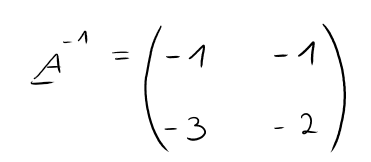
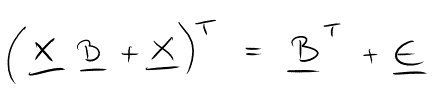
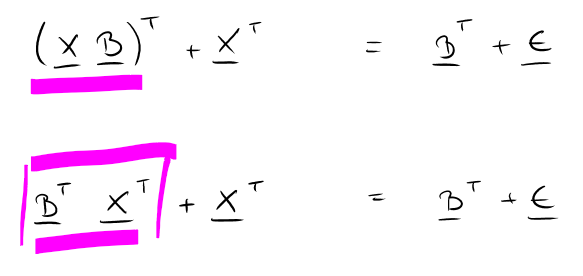
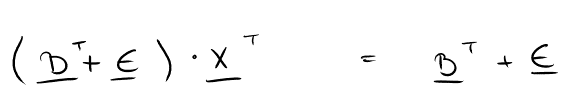
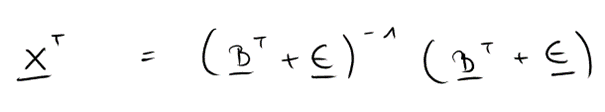
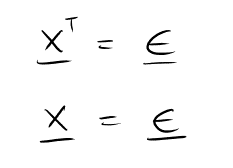
Im Multiplikationsbeispiel ist ein Fehler: C13 sollte 18 sein, 2×1 + 4×4.
Danke für den Kommentar. Du hast Recht. Wir haben den Fehler ausgebessert.