Ein Laplace-Experiment – im Mathematikunterricht begegnet man diesem Thema im Rahmen der Stochastik. Doch was versteht man eigentlich genau unter einem Laplace-Versuch? Die Antwort zu dieser Frage findest Du schnell und einfach im folgenden Artikel.
Im Folgenden erwartet Dich…
– … was überhaupt ein Laplace-Experiment ist,
– … was Nicht-Laplace-Experimente dementsprechend sind,
– … Beispiele zu Laplace-Experimenten
– … und schließlich Aufgaben zu Laplace-Experimenten zum Üben.
Laplace-Experiment Definition – so klappt das ganz simpel
Ein Laplace-Experiment ist ein Zufallsversuch mit besonderen Bedingungen. Es wurde nach dem Mathematiker Pierre-Simon Laplace benannt, der sich in seinem Leben u.a. mit der Wahrscheinlichkeitstheorie auseinandergesetzt hat. Welche Bedingungen ein Laplace-Versuch erfüllen muss, lernst Du im folgenden Kapitel.

Was ist ein Laplace-Experiment?
Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem alle Ereignisse, die eintreten können, genau dieselbe Wahrscheinlichkeit haben.
Um die Wahrscheinlichkeit von Ereignissen solcher Zufallsexperimente berechnen zu können, verwendet man die sogenannte “Laplace-Formel”.

Nicht-Laplace-Experimente
Nicht-Laplace-Experimente sind hingegen Zufallsexperimente, bei denen alle Ereignisse, die auftreten können, nicht dieselbe Wahrscheinlichkeit haben.
Beispiele für solche Nicht-Laplace-Experimente sind das Werfen einer Reißzwecke oder eines gezinkten Würfels.

Laplace-Experiment Beispiele – Schritt für Schritt erklärt
Betrachten wir zuerst einen normalen Würfel, der einmal geworfen wird.
Dieser Würfel hat sechs komplett gleich große Seiten mit sechs verschiedenen Zahlen.
Die Wahrscheinlichkeit, eine bestimmte Zahl bei einem Wurf zu würfeln, liegt also immer bei einem Sechstel.
Somit liegt in diesem Fall ein Laplace-Experiment vor.
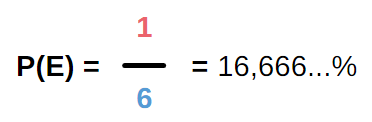

Was wäre aber, wenn man möchte, dass ein bestimmtes Ereignis auftritt?
Wie hoch wäre beispielsweise die Wahrscheinlichkeit, dass eine Zahl bei einmaligem Wurf gewürfelt wird, die höchstens drei beträgt?
Um diese Wahrscheinlichkeit zu berechnen, verwendet man ebenfalls die Laplace-Formel:

Es gibt drei mögliche Ereignisse, die die Bedingung der Aufgabenstellung erfüllen. Entweder wird eine 1, eine 2 oder eine 3 gewürfelt.
Das heißt, es gibt genau drei gewünschte Ereignisse, die auftreten können. Die Anzahl der möglichen Ereignisse beträgt hier immer sechs.
Der Quotient wird nach der Laplace-Formel gebildet und schon hat man das gewünschte Ergebnis.

Betrachten wir nun eine Münze, die einmal geworfen wird. Diese Münze hat zwei genau große Seiten mit je einem Symbol (“Kopf” oder “Zahl”).
Die Wahrscheinlichkeit, dass eine Seite nach einem Münzwurf oben sichtbar ist, beträgt immer 50 %. Hier liegt daher auch ein Laplace-Experiment vor.
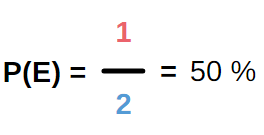
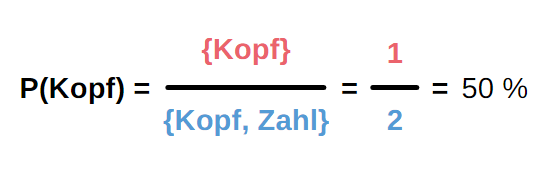
Wenn man bspw. nach einem Münzwurf “Kopf” oben sichtbar haben will, nutzt man zur Berechnung der Wahrscheinlichkeit wieder die Laplace-Formel.
Es gibt hier nur ein gewünschtes Ereignis, nämlich das, dass “Kopf” fällt.
Die Anzahl der möglichen Ereignisse ist hier immer zwei. Man bildet wieder den Quotienten und erhält das gewünschte Ergebnis.
Ein weiteres, etwas komplexeres, Beispiel ist das Casino Spiel Roulette. Die Wahrscheinlichkeit für jede Zahl auf dem Roulette Spielfeld ist genau gleich groß.
Wenn du auf eine bestimmte Farbe setzen würdest ist die 0 eine Besonderheit, weil sie die einzige Zahl ist ohne Farbe und damit immer ein Gewinn für das Casino darstellt.

Laplace-Experiment Aufgaben zum schnellen Vertiefen
Falls Du Deine erlernten Kenntnisse zum Thema “Laplace-Experiment” vertiefen möchtest, kannst Du hier anhand dieser Aufgaben dein erlerntes Wissen auf die Probe stellen.
Mithilfe der Lösungen kannst Du Deine Ergebnisse durch einen Klick auf das jeweilige Plus überprüfen. Weitere Aufgaben findest Du ansonsten im Link.
Aufgabe 1: Entscheide, ob es sich bei den folgenden Zufallsexperimenten um ein Laplace-Versuch handelt!
Ja, da die Wahrscheinlichkeit für das Auftreten eines Ereignisses beim Wurf eines normalen Würfels immer ca. 16,67 % beträgt.
Nein, da die Wahrscheinlichkeiten, dass die Reißzwecke nach dem Wurf auf dem Kopf oder auf der Seite landet, nicht gleich sind.
Nein, da es drei unterschiedlich große Felder gibt und somit die Wahrscheinlichkeiten für das Auftreten dieser Felder nicht gleich sein können.
Ja, da die Felder gleich groß und somit die Wahrscheinlichkeit für das Auftreten der verschiedenen Felder gleich sind.
Ja, da die Wahrscheinlichkeit für das Auftreten eines Ereignisses (“Kopf” oder “Zahl”) beim Wurf einer Münze immer 50 % beträgt.
Nein, da die Münze gezinkt ist und somit die Wahrscheinlichkeiten für das Auftreten eines Ereignisses (“Kopf” oder “Zahl”) nicht gleich sind.
Aufgabe 2: Du würfelst einmal einen normalen Würfel.
1
— = P(5) (Anwendung der Laplace-Formel)
6
2 1
— = — = P (x < 3) (Anwendung der Laplace-Formel)
6 3
3 1
— = — = P (x ≥ 4) (Anwendung der Laplace-Formel)
6 2
2 1
— = — = P (x = {2,6}) (Anwendung der Laplace-Formel)
6 3
5
— = P (x ≠ 1) (Anwendung der Laplace-Formel)
6
4 2
— = — = P (x ≠ {3,4}) (Anwendung der Laplace-Formel)
6 3
Laplace-Versuch: Häufig gestellte Fragen / FAQ
Ein Laplace-Experiment ist ein Zufallsversuch, bei dem alle möglichen Ereignisse genau die gleiche Wahrscheinlichkeit haben. Nicht-Laplace-Experimente sind Zufallsversuche, bei denen alle möglichen Ereignisse nicht die gleiche Wahrscheinlichkeit haben wie bspw. der Wurf einer Reißzwecke oder eines gezinkten Würfels.
Die möglichen Ereignisse beim Münzwurf sind, dass entweder “Kopf” oder “Zahl” geworfen wird. Beide Ereignisse können mit derselben Wahrscheinlichkeit von 50 % eintreten. Daher handelt es sich hier um ein Laplace-Experiment.
Nur wenn die Wahrscheinlichkeiten für das Eintreten aller Felder auf dem Glücksrad gleich sind, handelt es sich bei einem Glücksrad um ein Laplace-Experiment.
Um die Wahrscheinlichkeit von Laplace-Versuchen zu bestimmen, nutzt man die Laplace-Formel. Dabei wird die Anzahl der gewünschten Ereignisse durch die Anzahl der möglichen Ereignisse geteilt und man erhält die Wahrscheinlichkeit für ein bestimmtes Ereignis.
Die Laplace-Bedingung tritt ein, wenn die Standardabweichung größer als 3 ist. Die Standardabweichung dient als Maß dafür, wie weit die jeweiligen Zahlen verteilt bzw. wie weit die jeweiligen Messwerte durchschnittlich von dem Erwartungswert/Mittelwert entfernt sind.
Hat Dir der Inhalt geholfen? Lass uns gerne einen kurzen Kommentar da, wir würden uns sehr freuen! Ansonsten findest Du weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.

