Bei der großen Anzahl an mathematischen Formeln, die man zum Volumen berechnen im Kopf behalten muss, vergisst man leicht einen Multiplikator oder kommt einfach durcheinander.
Durch unsere Anleitung findest du wieder den roten Faden und weißt genau, wie man das Volumen der wichtigsten geometrischen Körper berechnet.
Los geht’s!
Volumen von geometrischen Körpern – Was ist das?
Volumen bezeichnet den räumlichen Inhalt eines geometrischen Körpers und wird auch Raum- oder Kubikinhalt genannt. Das Volumen kann dir z.B einen Einblick darin geben, wie viel Flüssigkeit in einen Körper passt.
Volumen der wichtigsten geometrischen Körper
Allgemein braucht man, um das Volumen eines Körpers zu berechnen, die Grundfläche des Körpers, die wir in den unteren Abbildungen gelb markiert haben, und die Höhe. Die Höhe ist dabei orthogonal (im 90° Winkel) zu der Grundfläche. Wenn die Grundfläche also in der Waagerechten liegt, misst die Höhe senkrecht dazu, wie hoch der Körper ist.
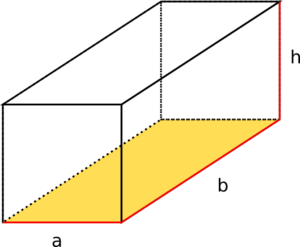
Volumen Quader berechnen
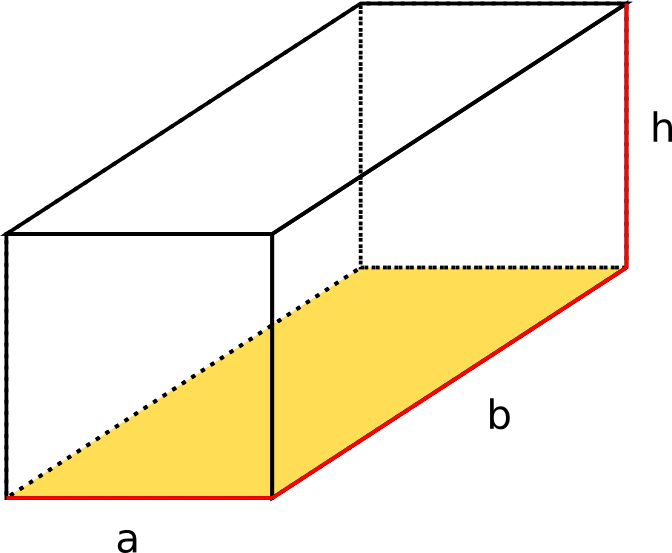
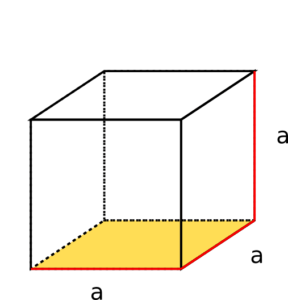
Ein Quader wird aus sechs Seitenflächen, die im rechten Winkel aufeinander stehen, zusammengesetzt. Die Flächen, die parallel zueinander liegen, sind kongruent (deckungsgleich).
Wenn die gelb markierte Grundfläche der Teppich in einem Zimmer ist, wäre die Decke des Zimmers also gleich groß.
Das Volumen (V) des Quaders berechnet sich so: . Um Die Grundfläche (G) zu bestimmen, wird die Länge (b) mit der Breite (a) multipliziert:
Es ergibt sich folgende Formel:
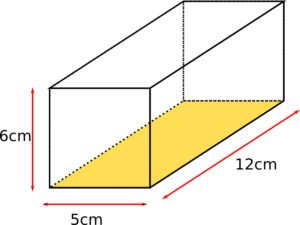
Berechne das Volumen des abgebildeten Quaders. Bestimme dafür zuerst die Größe der Grundfläche.
Die Grundfläche berechnen wir durch:
Um das Volumen zu erhalten, multiplizieren wir die Grundfläche mit der Höhe:
Volumen Würfel berechnen
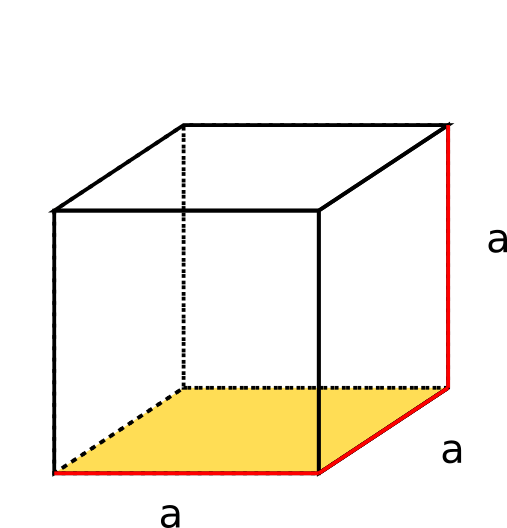
Der Würfel ist ein besonderer Quader. Alle seine Kanten sind gleich lang, sodass alle Seitenflächen deckungsgleich sind und wir Breite, Länge und Höhe gar nicht unterscheiden müssen. Wir benötigen nur eine Längenangabe.
Das Volumen (V) des Würfels berechnet sich so:
Berechne das Volumen eines Würfels mit einer Seitenlänge von 7cm.
Wie würden Breite, Länge und Höhe aussehen?
Das Volumen erhalten wir durch:
Breite, Länge und Höhe wären jeweils 7cm.
Volumen Pyramide berechnen
Allgemein wird eine Pyramide aus einem Vieleck als Grundfläche und einer je nach Vieleck variierenden Anzahl von Dreiecken zusammengesetzt. Wir schauen uns zwei Formen einer geraden Pyramide an. Gerade bedeutet in diesem Fall, dass die Spitze der Pyramide über dem Mittelpunkt der Grundfläche liegt.
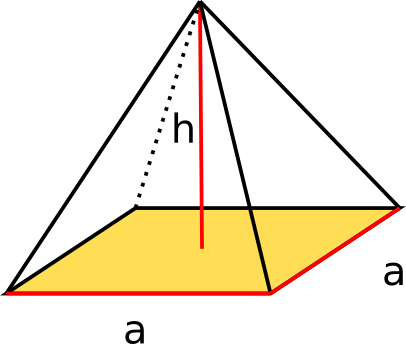
Die quadratische Pyramide
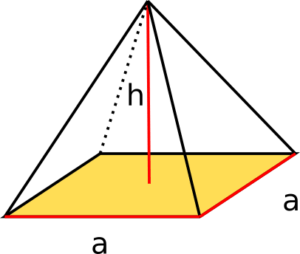
Die quadratische Pyramide hat als Grundfläche ein Quadrat, sodass Breite und Länge gleich sind.
Zur Berechnung des Volumens gilt bei Pyramiden allgemein:
Die quadratische Pyramide können wir also mit folgender Formel berechnen:
Berechne das Volumen einer quadratischen Pyramide mit h=4cm und a=8cm.
Das Volumen erhalten wir durch:
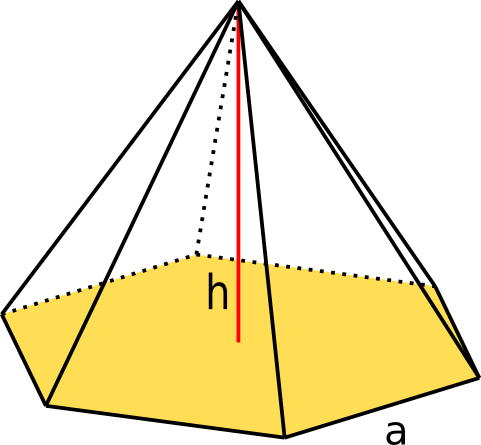
Die Pyramide mit einem regulären Sechseck
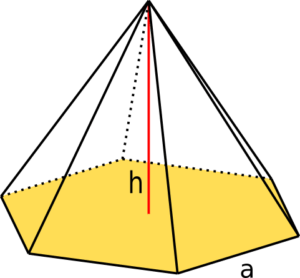
Die Pyramide mit einem regulären Sechseck hat als Grundfläche ein Sechseck, welches überall die gleiche Seitenlänge hat.
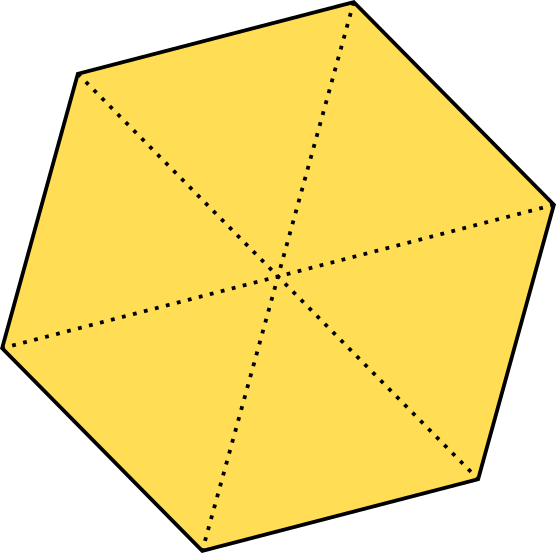
Um die allgemeine Volumenformel für Pyramiden anzuwenden, müssen wir zunächst den Flächeninhalt des Sechsecks berechnen können. Die Formel hierzu lautet:
Diese Formel ergibt sich dadurch, dass das Sechseck aus 6 gleichseitigen Dreicken besteht. Wenn du erfahren willst, wie diese Formel entstanden ist, klicke hier.
Daraus folgt diese Volumenformel:
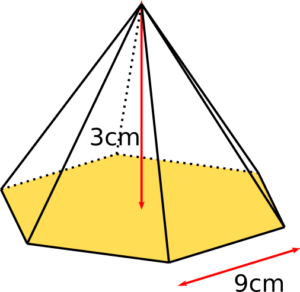
Berechne zunächst den Flächeninhalt des Sechsecks
und dann das Volumen der abgebildeten Pyramide.
Den Flächeninhalt berechnen wir so:
Damit erhalten wir ein Volumen von:
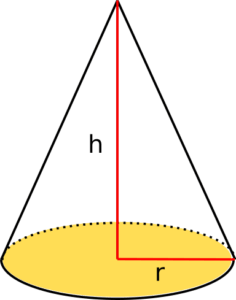
Volumen Kegel berechnen
Ein Kegel hat nur zwei Flächen und eine Spitze. Die Grundfläche ist hierbei rund. Um den Flächeninhalt der Grundfläche zu berechnen, brauchen wir nicht wie zuvor eine Seitenlänge, sondern den Radius (r).
Aus folgt für die Berechnung des Volumens:
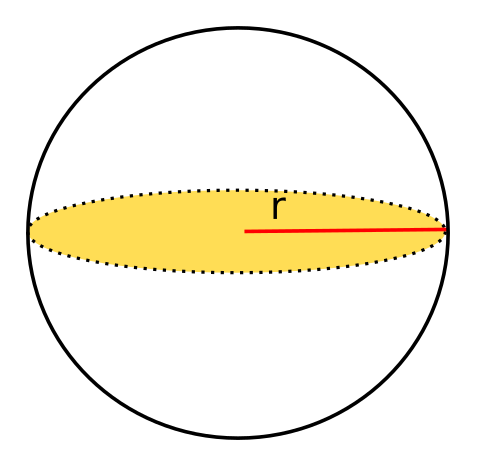
Volumen Kugel berechnen
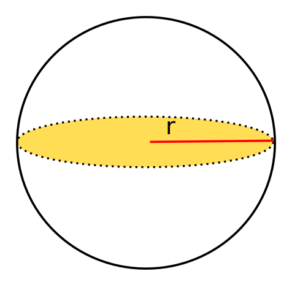
Die Kugel hat nur eine Fläche und keine Kanten. In diesem Ausnahmefall benötigst du nicht die Höhe. Ihr Volumen lässt sich wie folgt berechnen:
Falls du ganz genau wissen möchtest, wie du zu dieser Formel gelangst und sie dir herleitest, klicke hier. Wenn dich zudem interessiert, wie du den Umfang und die Oberfläche einer Kugel berechnest, schau hier vorbei.
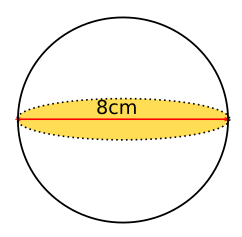
Berechne das Volumen der abgebildeten Kugel.
Zunächst musst du den Durchmesser halbieren:
Das Volumen erhalten wir durch:
Volumen Zylinder berechnen
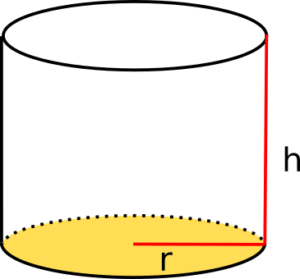
Ein Zylinder besteht aus drei Flächen. Die zwei Kreise, die sich gegenüberliegen, sind kongruent (gleich groß). Zunächst brauchen wir den Flächeninhalt der Kreise.
Aus folgt für die Berechnung des Volumens:
Falls dich auch interessiert, wie du die Oberfläche und dem Umfang eines Zylinders berechnest, schau hier vorbei.
Wenn der Durchmesser des des Zylinders 10cm und die Höhe 30cm beträgt, welches Volumen weist er dann auf?
Zunächst musst du den Durchmesser halbieren:
Das Volumen erhalten wir durch:
V = π · (5cm)² · 30cm ≈ 2356cm


Hab nochmal vor der Arbeit draufgeguckt. Hat sehr geholfen, Dankeschön?.
hallo
Wie rechnet man, wenn die Pyramide oben eine Fläche hat (v-Form mit oben und unten einer Ebene)?