4,35 von 5 Sterne
Loading...
Du möchtest einen Maßstab berechnen, aber weißt nicht wie? Maßstäbe begegnen uns oft im Leben, ob auf Stadtplänen, bei Modellen oder im Atlas. In diesem Artikel erklären wir dir…
… was ein Maßstab überhaupt ist
… wo und wie Maßstäbe angewendet werden
… wie du Maßstäbe bestimmst und
… wie du Maßstäbe umrechnen kannst
Außerdem findest du am Ende des Artikels Übungen, bei denen du direkt prüfen kannst, ob du alles verstanden hast.
Maßstab Definition
Ein Maßstab gibt dir die Größenverhältnisse von Dingen im Vergleich zur Realität an. Er sagt dir, wieviel mal größer oder kleiner etwas in echt ist als das, was du z.B. auf einem Plan siehst. Der Maßstab wird üblicherweise als 1:x oder x:1 angegeben. Das x ist in diesem Fall die Maßstabszahl.
Tipp:
1:x → etwas ist auf der Abbildung kleiner als in der Realität
x:1 → etwas ist auf der Abbildung größer als in der Realität
Die zwei Punkte (:) spricht man beim Maßstab als “zu”. Bei einem Maßstab von 1:10 sagt man also “diese Karte ist im Maßstab von 1 zu 10 gezeichnet”. In diesem Fall wäre etwas in der Realität 10 mal so groß und 1cm auf der Karte entspricht 10 cm in echt.
Meistens sind Maßstäbe am einfachsten mit Zentimetern (cm) zu handhaben, da das die praktischste Maßeinheit für Pläne, Karten und Modelle ist.
Karte, Modell, Grundriss – Arten von Größenverhältnissen
In der Schule findest du Maßstäbe wahrscheinlich am häufigsten in Erdkunde wenn ihr mit dem Atlas oder mit großen Karten arbeitet. Das bringt uns auch zu der wichtigsten Maßstabsart: dem Längenmaßstab.
Der Längenmaßstab gibt an, wie lang eine Strecke in Wirklichkeit ist. Eine weitere Maßstabsart ist der Höhenmaßstab. Er bezieht sich ebenfalls auf Strecken, jedoch sind sie hier vertikal, also hochkant.
Den Höhenmaßstab benutzt man meistens, um die Höhe von Bergen oder Gebirgen auf Landkarten anzugeben.
Der Längenmaßstab ist waagrecht, der Höhenmaßstab senkrecht
Es gibt auch noch den Flächen- und den Globusmaßstab. Diese beiden Arten werden jedoch nur sehr selten verwendet. Wir konzentrieren uns in diesem Artikel auf den Längenmaßstab.
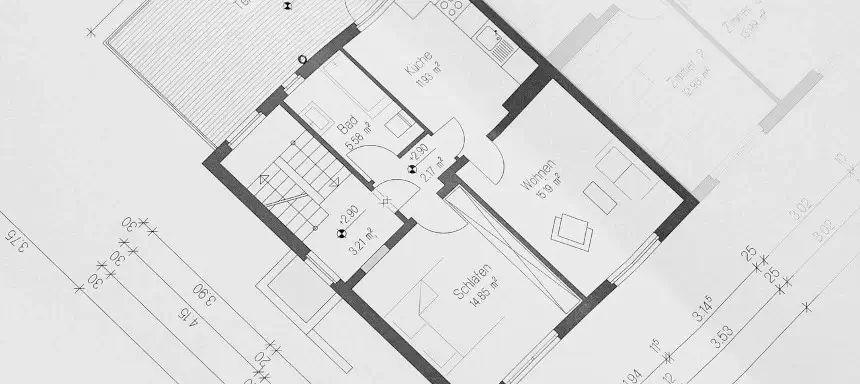
Vielleicht hast du auch schon mal den Grundriss von eurem Haus oder eurer Wohnung gesehen. Der Grundriss ist natürlich nicht so groß wie das Haus oder die Wohnung sondern so groß bzw. klein wie ein Blatt Papier.
Da jedes Objekt in unserer Welt vermessen werden kann, kann auch alles in unterschiedlichen Maßstäben gezeichnet, gebaut und dargestellt werden.
Wie erkläre ich Maßstab?
“Verhältnis zwischen […] Größen, besonders Strecken auf einer Landkarte, und den entsprechenden Größen in der Wirklichkeit”
Duden
Was ist ein Maßstab in der Geographie?
In der Geographie werden Maßstäbe sehr häufig verwendet, da Geographen oft Karten erstellen.
In einem Atlas zum Beispiel müssen große Länder oder Bereiche auf normalen Buchseiten abgebildet werden. Deshalb muss die Karte der Gegend verkleinert werden.
Damit bei diesem Prozess nichts schief läuft, werden Strecken wie Meter und Kilometer in cm und mm umgerechnet.
Und genau dazu verwendet man den Maßstab.
1:5 bedeutet: etwas ist in der Realität 5 mal so groß wie auf der Karte.
Maßstab berechnen mit Formel – einfache Erklärung für die Grundschule
Die Maßstabsbestimmung ist in ein paar einfachen Schritten getan. Dabei möchten wir den Maßstab einer Abbildung herausfinden, während wir wissen wie groß etwas auf dem Papier und in Wirklichkeit ist.
Nehmen wir an du siehst das Bild einer Schlange in einem Buch. Nun möchtest du wissen, in welchem Maßstab die Schlange abgebildet ist. Du weißt, dass sie in Wirklichkeit 60cm lang ist.
Frage: wie viel mal größer ist die Schlange in echt?
Wir beantworten unsere Frage Schritt für Schritt.
Als ersten Schritt misst du mit deinem Lineal die Länge der Schlange auf dem Bild. Nehmen wir an, du erhältst eine Größe von 5cm.
Fassen wir zusammen: Schlange in echt: 60cm. Schlange im Buch: 5cm.
Um den Maßstab richtig zu bestimmen, müssen beide Größen in der selben Einheit angegeben sein. Dies ist bei unserer Aufgabe zum Glück schon der Fall, beide Größen sind in cm. Wären die Längeneinheiten unterschiedlich, müssten wir eine davon noch umrechnen.
Du brauchst noch ein bisschen Hilfe beim Umrechnen von Längeneinheiten? Hier findest du Antworten.
Wir wissen, dass die Schlange in der Realität größer ist, als auf dem Bild. Das heißt also, dass der Maßstab in der Form 1:x geschrieben wird. Wir müssen nur das x rausfinden.
Um dies zu tun, dividieren wir ganz einfach die Größe in der Realität durch die Größe auf dem Bild.
Also: 60cm geteilt durch 5cm = 12 cm. Und dieses Ergebnis ist unser x.
Lösung: Der Maßstab der Abbildung ist dementsprechend 1:12 (“1 zu 12”). Die Schlange ist in echt 12 mal größer als auf dem Bild. 1cm auf dem Bild entsprechen also 12cm in der Realität.
Maßstab umrechnen
Das Ziel der Umrechnung eines Maßstabes ist eigentlich immer, herauszufinden, wie groß oder weit etwas in der Wirklichkeit ist.
Stell dir also vor, du hast deinen Atlas mit der Karte von Deutschland vor dir. Du möchtest die Strecke zwischen Frankfurt a.M. und Berlin in Kilometern bestimmen.
Mit deinem Lineal misst du deshalb als erstes den Abstand zwischen den Städten ab. Das sind ungefähr 12 cm.
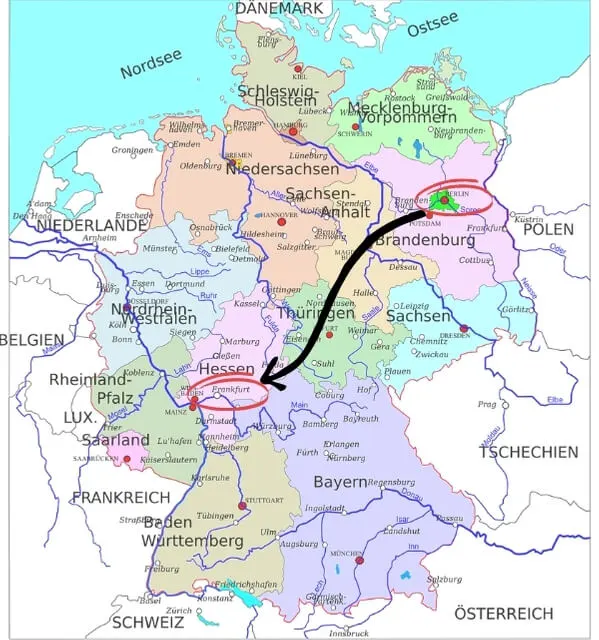
Als Maßstab ist 1:3.500.000 angegeben. Was heißt das also nun?
Das heißt, dass ein 1 cm auf der Karte 3.500.000 cm in der Realität entspricht.
Also 1cm auf der Karte = 3.500.000 cm in echt.
Da du die Strecke von 12 cm ausrechnen möchtest, multiplizierst du beide Zahlen mit 12. So erhältst du: 12cm auf der Karte = 42.000.000 cm in echt.
Unter 42.000.000 cm kann man sich jetzt erstmal nicht wirklich was vorstellen. Doch in zwei Schritten weißt du wie weit die Städte in der Realität auseinander liegen.
Zur Erinnerung: 100cm = 1m; 1.000m = 1km
Du musst jetzt nur noch die 42.000.000 cm in Kilometer umrechnen.
42.000.000 cm = 420.000 Meter = 420 Kilometer
Und schon hast du herausgefunden, dass Berlin und Frankfurt in echt ungefähr 420 Kilometer auseinander liegen.
1 zu 50, 1 zu 2,… – Beispiele für die Maßstabsberechnung mit Dreisatz
Im Folgenden erklären wir dir an gängigen Beispielen, wie du mit dem Maßstab rechnen kannst. Das geht ganz einfach mit dem Dreisatz. Den Dreisatz haben wir im vorherigen Absatz auch schon angewendet.
Maßstab 1 zu 50
Plan: in echt:
1cm → 50cm
10cm → 500cm
10cm → 5m
Maßstab 1 zu 2
Der Maßstab 1:2 bedeutet immer, dass die Realität doppelt so groß bzw. lang ist, wie sie abgebildet wurde. Hast du ein Modell von etwas, ist das Objekt in echt also exakt doppelt so groß. 1 cm am Modell entspricht 2 cm am wahren Objekt.
Maßstab 3 zu 1
Buch: in echt:
1cm → 1/3cm
3cm → 1cm
Maßstab 1 zu 100
Modell: in echt:
1cm → 100cm
50cm → 5000cm
50cm → 50m
Ein Zug, der in Wirklichkeit 50 Meter also 5.000cm lang ist, kann mit einem Modell nachgebaut werden, das nur 50cm lang ist.
Diese Grafik stellt nochmal unterschiedliche Maßstäbe bildlich da. Das größte Auto hat den Maßstab 1:1.
Die nächst kleinere Größe wird mit 1:2 angegeben. Dieses Auto ist also exakt halb so lang wie das Originalauto. So geht es immer weiter.
Wie du siehst, steigt die Maßzahl, je kleiner die Modelle werden.
Hier haben wir dir nochmal alle Rechenwege zusammengestellt, um einen Maßstab oder die Realität zu berechnen.
Hier kannst du dir die Übersicht auch nochmal runterladen.
Größenverhältnisse berechnen – Übungen mit Lösung
Versuche es nun einmal selbst! Lese dir die folgenden Aufgaben in den blauen Kästchen durch und stelle eine Berechnung auf. Danach kannst du dich mit der Lösung überprüfen.
Viel Erfolg!
Lösung
⇒ 15cm * 4 = 60cm
Die Strecke ist in echt 60cm lang
Lösung
⇒ 8cm * 1.500 = 12.000cm
Die Strecke ist in echt 12.000cm = 120m lang.
Lösung
⇒ 4cm / 8 = 0,5cm
Die Strecke ist in echt 0,5cm = 5mm lang.
Lösung
⇒ 18km = 18.000m = 1.800.000cm
1.800.000cm / 6cm = 300.000
Der Maßstab ist 1:300.000
Lösung
⇒ 5m = 500cm
500cm /10cm = 50
Der Maßstab ist 1:50
Lösung
⇒ 9cm = 90mm
90mm/6mm = 15
Der Maßstab ist 15:1
Toller Artikel. Er hat alles sehr gut erklärt. Das Bild mit den Autos gefällt mir sehr gut.
Lehrstoff einfach und verständlich, sodaß auch ein Opa mit 75 eine °Wiederholungsprüfung besteht!!
Danke gut gemacht!