Parallelogramm (2024) – Flächeninhalt, Umfang & Eigenschaften erklärt!

In diesem Artikel findest du alle wichtigen Informationen zum Parallelogramm einfach erklärt.

Hier erfährst du …

• was ein Parallelogramm ist
• welche Eigenschaften ein Parallelogramm hat
• wie du den Umfang berechnen kannst
• wie du den Flächeninhalt berechnen kannst
• wo der Mittelpunkt eines Parallelogramms ist
• was der Unterschied zu anderen Vierecken ist

Beginnen wir gleich mit dem ersten Punkt:

Was ist ein Parallelogramm?

Ein Parallelogramm ist eine zweidimensionale geometrische Figur aus der Familie der Vierecke. Seine Besonderheit ist, dass die einander gegenüberliegenden Seiten zueinander parallel verlaufen.

Die Ecken werden mit Großbuchstaben in alphabetischer Reihenfolge gegen den Uhrzeigersinn benannt. Für die Seiten gilt das Gleiche, nur eben mit kleinen Buchstaben.

Die vier Winkel des Parallelogramms werden entsprechend den Großbuchstaben ihrer jeweiligen Ecken mit den entsprechenden kleinen Buchstaben des griechischen Alphabets benannt.

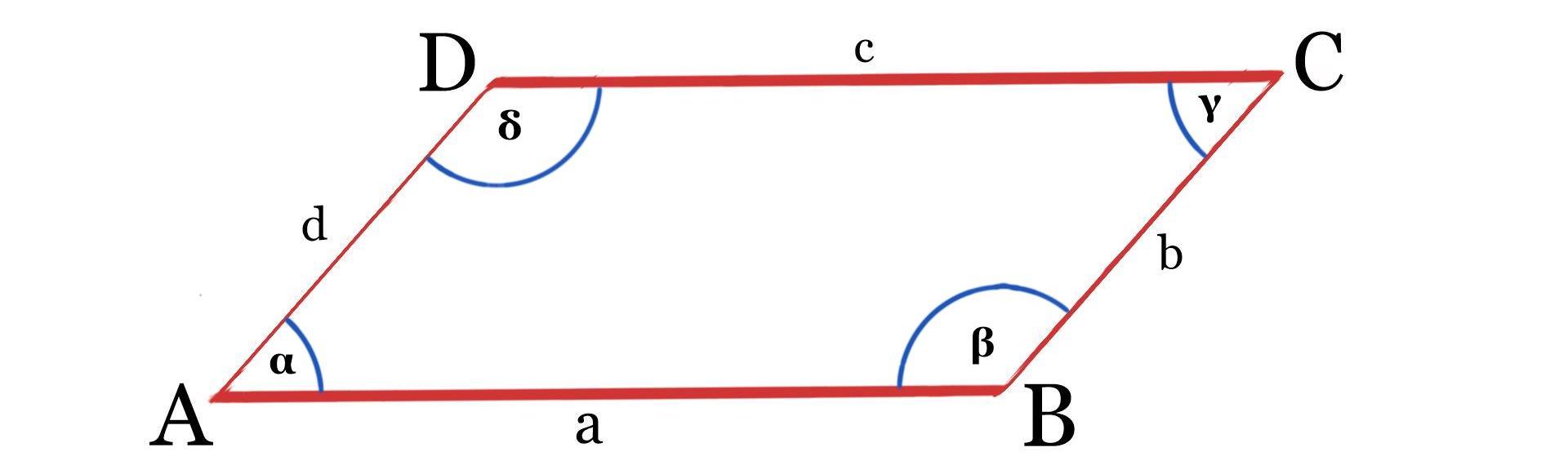
Sehen wir uns als Nächstes die Eigenschaften an:

Eigenschaften

Ein Parallelogramm hat:

1. Vier Ecken (A, B, C, D)
2. Vier Seiten (a, b, c, d)
3. Jeweils zwei Paar parallel verlaufender Seiten
   a ist parallel zu c (a ll c)
   b ist parallel zu d (b ll d)
4. Jeweils zwei Paar gleich lange Seiten
   a ist genauso lang wie c
   b ist genauso lang wie d
5. Vier Winkel (α, β, γ, δ)
   alle Winkel zusammen ergeben 360°
   nebeneinander liegende Winkel ergeben zusammen 180°
   die einander gegenüberliegenden Winkel sind gleich groß
6. Einen Mittelpunkt
   um den Mittelpunkt ist das Parallelogramm punktsymmetrisch

Umfang des Parallelogramms berechnen

Der Umfang lässt sich ganz einfach berechnen. Dafür musst du einfach nur die Länge aller vier Seiten addieren.

Weil die gegenüberliegenden Seiten genau gleich lang sind, kannst du den Umfang auch berechnen, wenn du nur die Länge von zwei aneinander grenzenden Seiten kennst. Zum Beispiel a und b oder b und c.

Flächeninhalt des Parallelogramms berechnen

Um den Flächeninhalt berechnen zu können, musst du die Höhe des Parallelogramms kennen.

Die Höhe ermittelst du dadurch, dass du dir eine Seite aussuchst und dir eine Strecke denkst, die ihren Anfangspunkt auf dieser Seite hat und sie im rechten Winkel schneidet. Die gegenüberliegende Seite bildet den Endpunkt der Strecke. Die Länge der Strecke ist die Höhe des Parallelogramms.

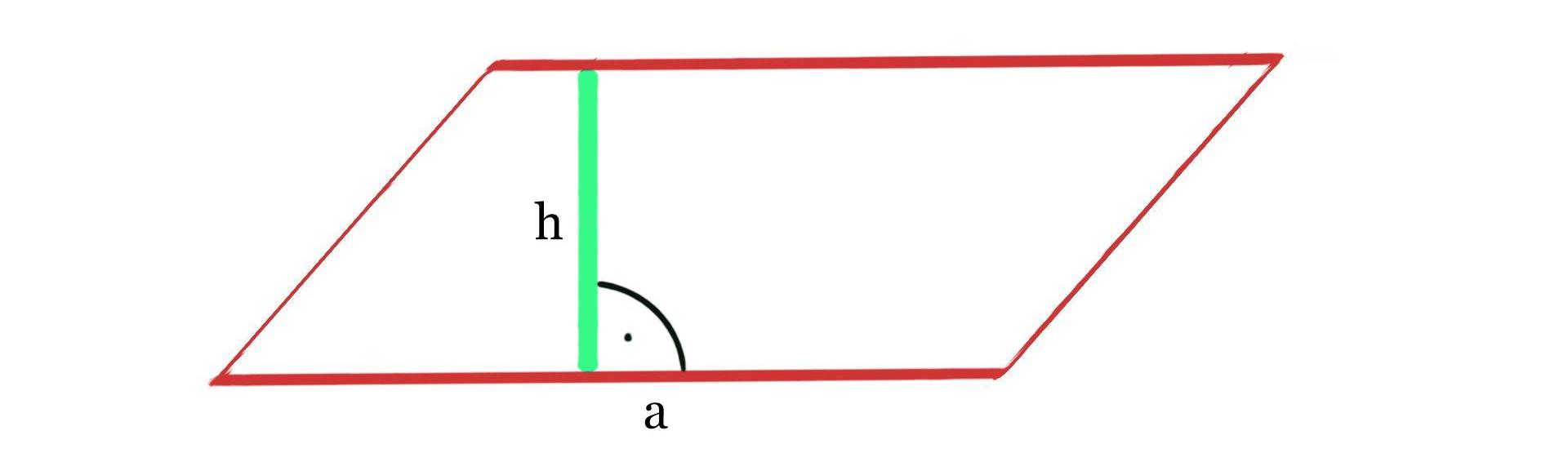
Die Formel ist jetzt ganz leicht zu berechnen:

Achtung: Die Höhe des Parallelogramms verändert sich, wenn du eine andere Seite als Ausgangspunkt wählst. Wenn du die Höhe ausgehend von der Seite b ermittelst, musst du diese Höhe auch mit der Seite b multiplizieren, um den richtigen Flächeninhalt zu erhalten.

Mittelpunkt ermitteln

Um den Mittelpunkt zu bestimmen, musst du zwei Diagonalen einzeichnen. Diese Diagonalen werden meistens als e und f bezeichnet. Sie reichen von einem Eckpunkt zum jeweils gegenüberliegenden Eckpunkt. Also schneidet eine Diagonale A und C, die andere B und D.

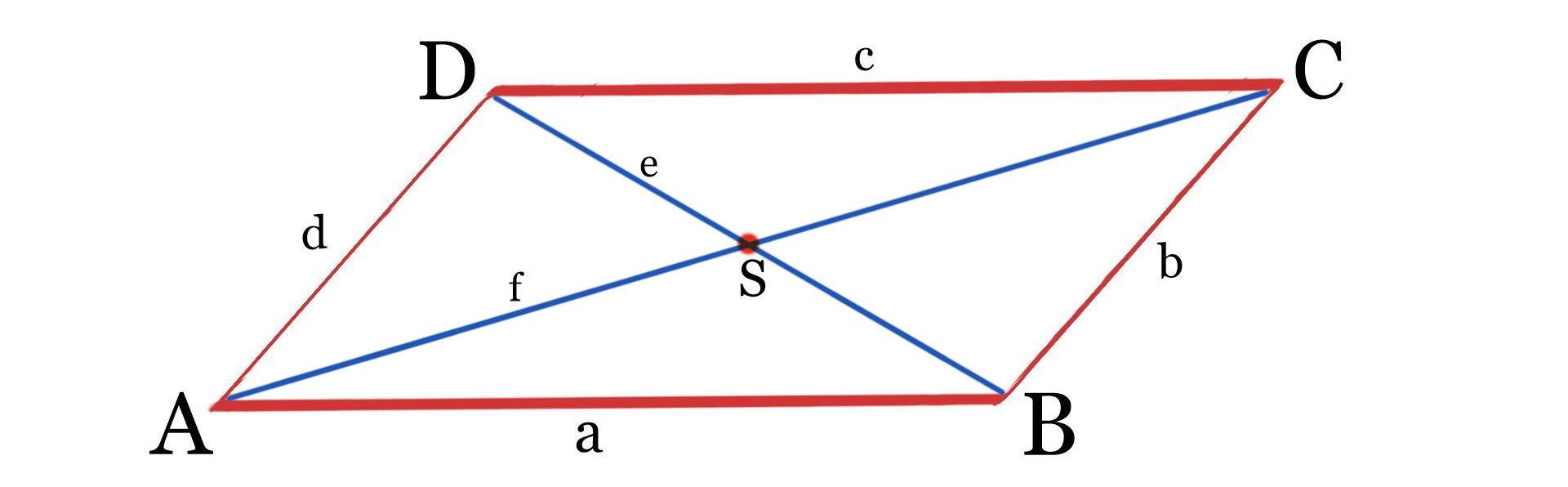
Der Mittelpunkt liegt an der Stelle, an der sich die beiden Diagonalen schneiden und ist das punktsymmetrische Symmetriezentrum des Parallelogramms.

Vergleich mit anderen Vierecken

Das Quadrat ist eine besondere Form des Parallelogramms, weil es zusätzlich noch die Eigenschaften hat, dass alle Seiten gleich lang sind und alle Winkel 90° haben.

Rechtecke und Rauten sind ebenfalls besondere Parallelogramme. Bei Rechtecken ist die zusätzliche Eigenschaft, dass alle Winkel rechte Winkel sind und an Rauten ist besonders, dass alle Seiten gleich lang sind.

Alle Quadrate, Rechtecke und Rauten sind Parallelogramme. Aber nicht alle Parallelogramme sind Quadrate, Rechtecke oder Rauten.

Parallelogramme sind immer auch Trapeze. Trapeze benötigen nur ein Paar parallele Seiten. Deshalb sind Parallelogramme eine besondere Form des Trapezes.

Grundsätzlich sind alle Parallelogramme Vierecke, weil sie 4 Ecken und 4 Seiten haben.

Alle Parallelogramme sind Trapeze und Vierecke. Aber nicht alle Trapeze und Vierecke sind Parallelogramme.

Übungsaufgaben

Jetzt haben wir noch 2 Übungsaufgaben vorbereitet, um dein Wissen zu testen. Wenn du dir bei den Lösungen unsicher bist, kannst du dir natürlich auch die Lösung ansehen.

Aufgabe 1

gegeben: a = 3 cm , d = 5 cm

gesucht: Umfang

Aufgabe 2

gegeben: b = 4 cm , Höhe von d = 7 cm

gesucht: Flächeninhalt

FAQ