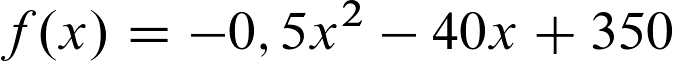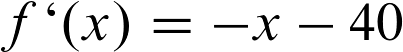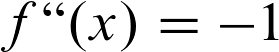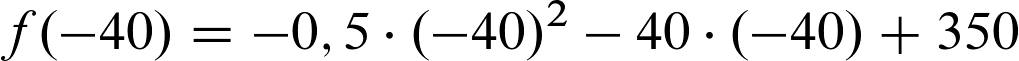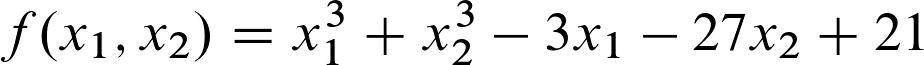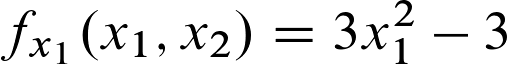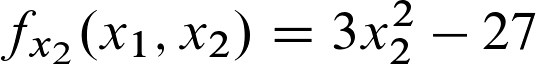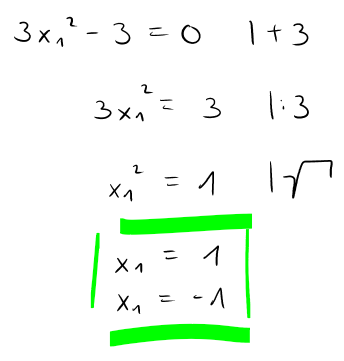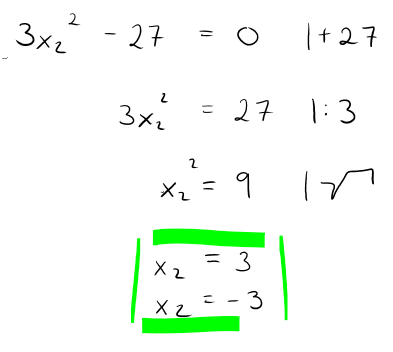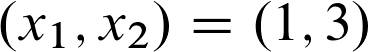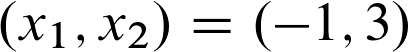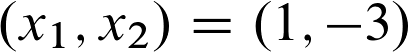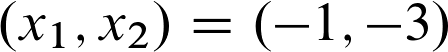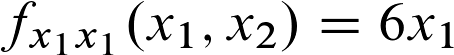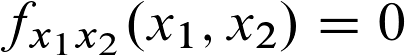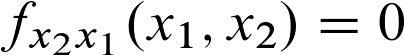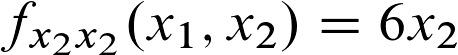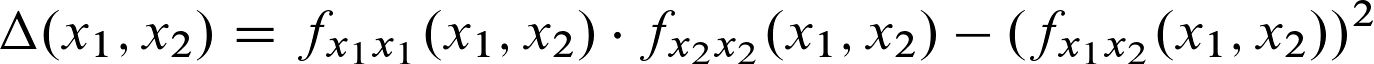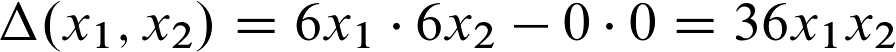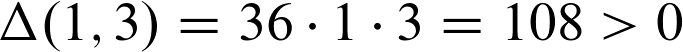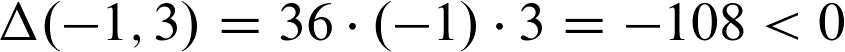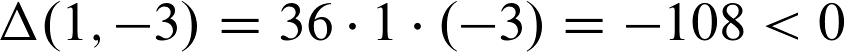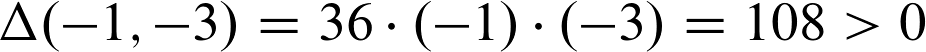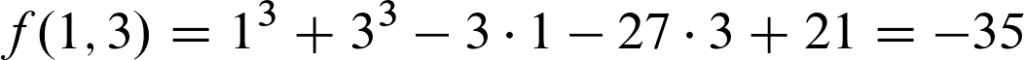4,33 von 5 Sterne
Loading...
Die Extremwertaufgabe ist ein recht umfangreiches Thema, wenn alles abgeklappert werden soll. Aber mach dir nichts draus! Mit diesem Artikel möchte ich dir zeigen…
… was Extremwerte sind,
… wie die Berechnung mit einer unabhängigen Variable (eindimensional) funktioniert,
… dazu noch, wie die Berechnung mit zwei unabhängigen Variablen (mehrdimensional) abläuft
… und zum Schluss die Berechnung von Extrema unter Nebenbedingung (bedingte Extrema)
Wir werden das anhand von kleinen Beispielen Schritt-für-Schritt durchgehen und danach wird dir das Thema bestimmt schon leichter fallen. Also lass uns gleich anfangen!
Fangen wir erst einmal mit der Erklärung von ein paar Begriffen an. Wenn du diese schon kennst, dann kannst du einfach weiter runterscrollen.
Was sind Extremwerte?
Es wird eine bestimmte Umgebung betrachtet, in der der größte bzw. kleinste Funktionswert gefunden werden muss.
Der kleinste Wert wird lokale Minimumstelle (lokales Minimum) und der größte Wert lokale Maximumstelle (lokales Maximum) genannt.
Es gibt auch die sogenannten globalen Extrema, die den größten bzw. kleinsten Wert innerhalb der gesamten Intervallgrenze darstellen (globales Maximum bzw. Minimum).
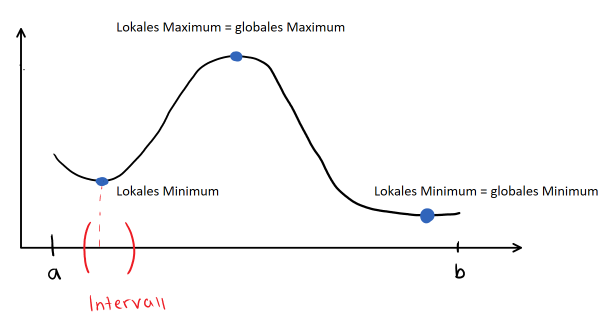
Ich habe dir hier eine kleine Grafik mitgebracht, damit du den Unterschied mal siehst.
Die für dich wichtigen Punkte sind blau in der Grafik markiert. Das a und b kennzeichnen Intervallgrenzen, die rote Klammer das Intervall (die Umgebung, welche wir betrachten sollen).
Das Intervall zeigt auf, dass kein anderer Funktionswert kleiner ist als der markierte. Somit ist die linke Extremstelle ein lokales Minimum – also der kleinste Funktionswert in der betrachteten Umgebung.
Wenn wir uns die gesamte Intervallgrenze anschauen, können wir sehen, welche Funktionswerte die absolut größten und niedrigsten sind. Das sind dann die globalen Extrema.
Was ist nun eine Extremwertaufgabe?
Hier geht es jetzt darum, die oben angesprochenen Extremwerte herauszufinden und zu berechnen. Das werden wir jetzt in den nächsten Abschnitten zusammen machen. Die Unterscheidung erfolgt hierbei nach eindimensionalen und mehrdimensionalen Extremwertaufgaben.
Um klein anzufangen, starten wir erstmal mit den eindimensionalen.
Extremwertaufgabe mit einer unabhängigen Variable
Wichtig ist: du musst zum Thema Ableitung fit sein.
Ich habe dir hier deshalb noch einen Link zu unserem Artikel über Ableitungsregeln reingestellt. Falls du da noch Hilfe gebrauchen solltest, schau gerne mal vorbei!
Jetzt geht es an die erste Beispielaufgabe. Wir werden das Schritt-für-Schritt zusammen durchgehen.
Eine gute Nachricht für dich: die Berechnung verläuft nach einer festen Schrittfolge. Wenn du die also ausreichend lernst, wirst du die Aufgabe in Zukunft auch bearbeiten können.
Beispiel zur Berechnung
Gegeben ist uns folgende Gleichung:
Der erste Schritt ist jetzt, die erste Ableitung der Gleichung zu berechnen.
Als zweiten Schritt, setzen wir die erste Ableitung = 0 und lösen (wenn möglich) nach x auf (Dieser Schritt ist die “notwendige Bedingung” bei der Berechnung einer Extremstelle).
Wir schreiben also:
Die -40 wird auf die andere Seite geholt, indem +40 gerechnet wird.
Das Ganze wird jetzt mit -1 multipliziert und wir bekommen folgendes Endergebnis:
Der berechnete x-Wert wird als “stationäre Stelle” bezeichnet (oder auch extremstellenverdächtig)
Der dritte Schritt ist nun, die zweite Ableitung unserer Gleichung zu berechnen.
Im vierten Schritt soll die stationäre Stelle (aus Schritt 2) überprüft werden, um welche Art von Extremwert es sich handelt (die sogenannte hinreichende Bedingung).
Eigentlich würdest du hier den x-Wert in die zweite Ableitung einsetzen und berechnen. Allerdings haben wir in der zweiten Ableitung kein x mehr, weshalb du das weg lassen kannst.
Somit ist das Ergebnis für unseren vierten Schritt:
Für die Überprüfung gilt jetzt folgendes:
zweite Ableitung < 0 → lokale Maximumstelle
zweite Ableitung > 0 → lokale Minimumstelle
Die -1 ist kleiner als 0, weshalb ein lokales Maximum an der Stelle x = -40 existiert.
Der fünfte und letzte Schritt wäre nun, den Extremwert zu berechnen.
Um das zu tun, setzt du die stationäre Stelle (Schritt 2) in die Ausgangsgleichung ein.
Als Endergebnis haben wir: 1.150 als Extremwert berechnet.
Das war es auch schon!
Wie du siehst: wenn du die Ableitungen und die Schrittfolge übst, kannst du ganz leicht einen Extremwert berechnen!
Übersicht der Schrittfolge
Ich schreib dir hier die Schrittfolge nochmal im Gesamten auf.
- Erste Ableitung berechnen
- Notwendige Bedingung: setze die erste Ableitung = 0 und berechne das Ergebnis (=stationäre Stelle)
- Berechne die zweite Ableitung
- Setze die stationäre Stelle (Schritt 2) in die zweite Ableitung ein, berechne das Ergebnis und prüfe:
- Berechne den Extremwert, indem die stationäre Stelle (Schritt 2) in die Ausgangsgleichung eingesetzt wird.
Und falls du sie dir noch herunterladen möchtest, dann gibt es die Schrittfolge als PDF-Dokument.
Berechnung bei Wendepunkten
Als kleiner Zusatz für dich, falls du das mal brauchen solltest.
Um das berechnen zu können, geht man genau so vor, wie oben auch. Die stationäre Stelle wird in die zweite oder dritte Ableitung eingesetzt, um das Endergebnis berechnen zu können.
Im nächsten Abschnitt geht es jetzt mit mehrdimensionalen Extremwertaufgaben weiter. Wenn du das nicht brauchst, dann scroll einfach weiter, bis zu den bedingten Extrema.
Extremwertaufgabe mit mehreren unabhängigen Variablen
Um diese Aufgabe bearbeiten zu können, musst du die partiellen Ableitungen beherrschen.
Wir haben zum Thema partielle Ableitung einen eigenen Artikel erstellt. Wenn du deine Erinnerung nochmal auffrischen möchtest, schau dort gerne mal vorbei!
Also gut, dann lass uns mal das Verfahren anhand eines Beispiels durchgehen.
Hier auch wieder eine gute Nachricht: es gibt ebenfalls ein Berechnungsschema, welches man durchgeht. Wenn du das verinnerlichen kannst, sollte also nichts mehr schief gehen!
Beispiel zur Berechnung
Für unser Beispiel nehmen wir mal folgende Gleichung zur Hand:
Der erste Schritt besteht nun darin, die partiellen Ableitungen erster Ordnung zu berechnen.
Wir erhalten also folgende Ergebnisse:
Im zweiten Schritt wird die notwendige Bedingung für eine Extremstelle geprüft.
Hierfür nimmst du die partiellen Ableitungen erster Ordnung zur Hand und setzt diese = 0. Das entstandene Gleichungssystem gilt es nun zu berechnen.
Wir erhalten also folgende Stellen:
für x1 : 1 und -1
für x2: 3 und -3
Falls du dir die Rechenwege nochmal anschauen möchtest, gibt es die hier für dich zum Ausklappen:
Rechenweg für Schritt 2
Für die partielle Ableitung erster Ordnung nach x1:
Für die partielle Ableitung erster Ordnung nach x2:
Da jede Stelle mit jeder kombiniert werden muss, erhalten wir in Summe vier stationäre Stellen:
Damit ist der zweite Schritt abgeschlossen und wir können zum nächsten übergehen.
Im dritten Schritt muss nun die partielle Ableitung zweiter Ordnung berechnet werden.
Wir nehmen also die Ableitungen erster Ordnung zur Hand und leiten diese abermals ab. Die Ergebnisse würden dann lauten:
Für die erste Gleichung:
Und für die zweite Gleichung:
Im vierten Schritt geht es nun darum, die stationäre Stelle zu überprüfen.
(das ist hier die hinreichende Bedingung für eine Extremstelle)
Hierfür gibt es zwei Möglichkeiten:
- hast du zwei Variablen (wie hier bei uns im Beispiel), dann kannst du auch die Delta-Funktion nehmen,
- gibt es mehr als zwei Variablen, kommt die Hesse-Matrix und das Prüfen auf Definitheit zum Einsatz
Da unser Beispiel nur zwei Variablen hat, werde ich mit der Delta-Funktion weiter machen. Diese lautet:
Wenn wir das nun mit unseren Werten füllen, kommt folgende Berechnung dabei raus:
Jetzt kommen wir zum eigentlichen Teil, nämlich, jede stationäre Stelle zu überprüfen.
Wir nehmen dafür unsere Delta-Funktion zur Hand, setzen die Werte für x1 und x2 ein und berechnen das Ergebnis.
Im Anschluss wird das Ergebnis auf folgendes geprüft, um eine endgültige Aussage treffen zu können:
Machen wir das Ganze nun mal anhand der stationären Stelle (1,3)
Wir befinden uns also bei dem Fall, dass die Delta-Funktion einen Wert über Null besitzt.
Deshalb nehmen wir jetzt die Ableitung zweiter Ordnung zur Hand (nach x1,x1) und setzen unsere Werte für x1 und x2 dort ein.
Da wir kein x2 haben, lautet die Rechnung 6 * 1 = 6.
Der Wert ist größer als Null, weshalb wir sagen können, dass es sich bei (1,3) um eine lokale Minimumstelle handelt.
Hervorragend! Das gleiche Verfahren wird jetzt für die restlichen stationären Stellen durchgeführt.
Wenn du magst, kannst du dir gerne mal Zettel und Stift zur Hand nehmen und die restlichen stationären Stellen überprüfen. Die übrig gebliebenen sind: (-1,3), (1,-3) und (-1,-3).
Die Lösungen sind hierunter bereitgestellt. Also klick sie einfach an, wenn du soweit bist.
Lösungen - Schritt 4
Für die Stelle (-1,3) lautet die Rechnung:
Hier haben wir nun den Fall, dass das Ergebnis der Delta-Funktion kleiner als Null ist. Aus diesem Grund können wir sagen, dass die Stelle (-1,3) eine Sattelpunktstelle ist.
Bei (1,-3) lautet die Rechnung:
Hier haben wir wieder den gleichen Fall, wie oben auch. Aus diesem Grund können wir also festlegen, dass die Stelle (1,-3) ebenfalls eine Sattelpunktstelle ist.
Zuletzt müssen wir die Stelle (-1,-3) überprüfen. Die Rechnung lautet also:
Hier haben wir wieder den Fall, dass das Ergebnis größer als Null ist. Also nehmen wir wieder die partielle Ableitung zweiter Ordnung (nach x1,x1) zur Hand, setzen die Werte für x1 und x2 ein und berechnen das Ergebnis.
Da bei der Ableitung kein x2 vorhanden ist, lautet die Rechnung: 6 * (-1) = -6.
Der Wert ist kleiner als Null, weshalb wir sagen können, dass die Stelle (-1,-3) eine lokale Maximumstelle ist.
Jetzt können wir mit dem fünften und letzten Schritt weiter machen.
Hier ist es wieder das gleiche Verfahren, wie bei der eindimensionalen Berechnung auch. Die stationäre Stelle wird in die Ausgangsgleichung eingesetzt, um somit den Extremwert berechnen zu können.
Wir nehmen also die Stellen (1,3) [lokales Minimum] und (-1,-3) [lokales Maximum], setzen diese in die Ausgangsgleichung ein und können somit die beiden Extremwerte berechnen.
Wenn wir das für unsere Stellen nun durchführen, kommen wir auf folgende Ergebnisse:
Und fertig sind wir!
Ich stelle dir hier nochmal eine kleine Übersicht bereit, damit du die Schrittfolge beisammen hast.
Übersicht der Schrittfolge
Fassen wir das Ganze nochmal zusammen:
- Partielle Ableitung erster Ordnung berechnen
- Notwendige Bedingung: setze die partielle Ableitung erster Ordnung = 0 und berechne das Ergebnis (=stationäre Stelle).
(Falls du die Wurzel ziehen musst, denk daran, alle Lösungen mit aufzuschreiben.) - Berechne die partielle Ableitung zweiter Ordnung
- Hinreichende Bedingung: überprüfen ALLER stationären Stellen.
5. Berechne den Extremwert, indem die stationären Stellen in die Ausgangsgleichung eingesetzt werden (achte dabei auf die Aufgabenstellung und nach was dort genau gefragt wird).
Ich habe dir hier ebenfalls die Schrittfolge als PDF-Dokument zusammengestellt. Du kannst sie dir also gerne auch herunterladen und damit dann arbeiten.
Extremwertaufgabe mit Nebenbedingung (bedingte Extrema)
Bei diesem Aufgabentyp hast du eine Zielfunktion und Nebenbedingungen gegeben. Du wendest die gleiche Schrittfolge an, wie bei der mehrdimensionalen Extremwertaufgabe.
Allerdings gibt es davor noch etwas anderes zu tun.
Nimm dir eine Nebenbedingung zur Hand und löse sie nach einer beliebigen Variable auf.
- du kannst hier entscheiden, welche das sein soll. Such dir eine aus, die am Einfachsten zu berechnen ist.
Das Ergebnis setzt du nun in die Zielfunktion ein und berechnest diese.
- somit hast du am Ende nur noch eine Unbekannte
Jetzt rechnest du mit der “normalen” Schrittfolge weiter
- dafür nimmst du deine “neue” Zielfunktion zur Hand
- und dann geht es ganz normal weiter, mit der Schrittfolge für die jeweilige Extremwertaufgabe.
- Zusatz: in Schritt 2 der normalen Schrittfolge, hast du eine Variable berechnen können. Setze diesen Wert einfach in die Gleichung der fehlenden Variable (siehe Schritt 1) ein, um die andere herauszufinden.
Wenn du bei Schritt 5 angekommen bist, um den Extremwert zu berechnen:
Du errechnest ja die unbekannten Variablen vorher schon aus. Die Werte werden in diesem Schritt wieder in die Ausgangsgleichung eingesetzt und nach dem gewohnten Verfahren berechnet.
Zusammenfassung – Extremwertaufgabe
Du hast in diesem Artikel also gelernt:
- die Berechnung einer Extremwertaufgabe mit einer Variable (eindimensional)
- wie die Berechnung bei zwei Variablen (mehrdimensional) abläuft (mithilfe der Delta-Funktion)
- und was du tun musst, um eine Extremwertaufgabe mit Nebenbedingung zu lösen
Das gute ist, dass es eine feste Schrittfolge gibt, nach der die Aufgaben zu berechnen sind. Wenn du die verinnerlicht hast, wird das Thema für dich leichter sein.
Sonst muss die Ableitung sitzen, sodass auch die partiellen Ableitungen kein Problem mehr für dich darstellen. Das Ganze musst du einfach bis zum Geht-nicht-mehr üben.
Hat dir der Artikel helfen können?
Wir haben uns bei diesem Artikel viel Mühe gegeben, um dir das Thema näher zu bringen. Also teile uns gerne mit, ob und wie der Artikel dir weiter helfen konnte.
Vielen Dank!
4,33 von 5 Sterne
Loading...
