Du kennst Koordinatensysteme aus der Schule, hast aber noch Fragen zu diesem Thema?
In diesem Artikel erklären wir dir an Hand von Beispielen, was ein Koordinatensystem ist, welche Unterschiede es zwischen den verschiedenen gibt, was die Quadranten sind und wie du ganz einfach Punkte ablesen, bzw. eintragen kannst.
Lass uns starten!
Ein Koordinatensystem hilft dir bei der Darstellung von Punkten oder anderen geometrischen Elementen, indem du diese an Hand von Zahlen, den Koordinaten, eindeutig zuordnen kannst.
Das Koordinatensystem, das du am häufigsten benutzt, hat zwei Achsen, die x-Achse und die y-Achse. Es gibt aber auch den einfachen Zahlenstrahl, der nur eine Achse hat oder auch dreidimensionale Koordinatensysteme, wo es noch eine dritte Achse gibt.
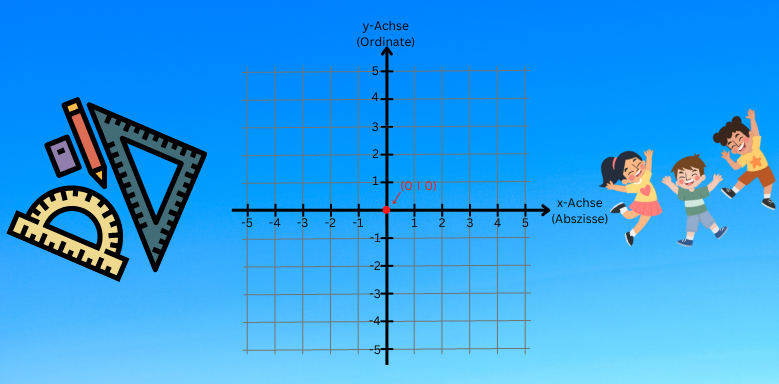
Jedes Koordinatensystem hat einen Nullpunkt. Beim Zahlenstrahl ist es die Koordinate 0 oder beim klassischen zweidimensionalen Koordinatensystem ist es der Punkt mit den Koordinaten (0, 0). Dieser wird als Koordinatenursprung (kurz: Ursprung) bezeichnet.
Aufbau
Damit du das ganze nachvollziehen kannst, betrachten wir erst einmal einen Zahlenstrahl:
Wie du sehen kannst, geht unser Zahlenstrahl von -10 bis 10. Hier kannst du schon direkt eine der Eigenschaften erkennen. Der Abstand zwischen den Zahlen ist immer gleich groß. Einen Wert wie 4 kannst du hier leicht einzeichnen oder ablesen.
Hast du aber einen Punkt mit zwei oder mehr Koordinaten gegeben, dann kannst du diesen nicht mehr auf dem Zahlenstrahl eintragen. Dafür brauchst du dann ein Koordinatensystem mit zwei Zahlenstrahlen, der x- und y-Achse.
Dieses zweidimensionale Koordinatensystem wird auch als kartesisches Koordinatensystem bezeichnet, nach dem französischen Mathematiker René Descartes. Hast du so ein System gegeben, hat dieses die folgenden Eigenschaften:
Eigenschaften
Die waagerechte Achse ist die x-Achse und wird auch als Abszisse bezeichnet
Die senkrechte Achse ist die y-Achse oder Ordinate
Der Schnittpunkt von x-Achse und y-Achse ist der Koordinatenursprung O(0∣0)
Abstände zwischen den Zahlen müssen auf den Achsen gleich groß sein. Das heißt, du kannst auf der x-Achse einen anderen Abstand zwischen den Werten wie auf der y-Achse haben
Koordinatensystem Quadranten
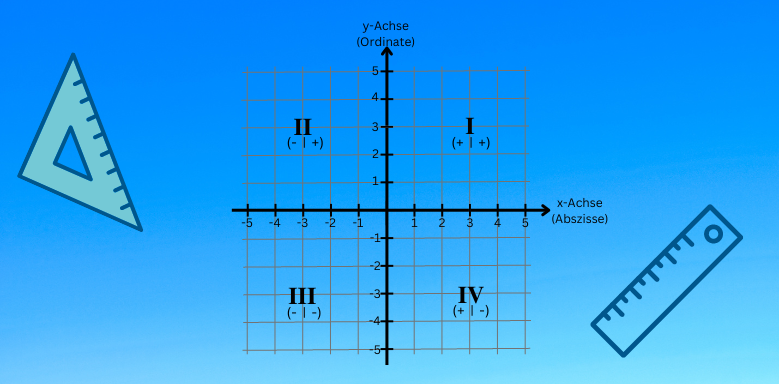
Das Koordinatensystem ist in vier Quadranten unterteilt. Die Aufzählung beginnt oben rechts und sie werden gegen den Uhrzeigersinn aufgezählt. Getrennt werden die einzelnen Quadranten von den Koordinatenachsen.
Für die vier Quadranten gilt:
x und y sind größer 0 (positive Zahlen) im I. Quadranten
Im II. Quadranten ist x<0 (negative Zahl) und y>0 (positive Zahl)
Sowohl x als auch y sind im III. Quadranten kleiner als 0 (negative Zahlen)
Im IV. Quadranten ist x>0 (positive Zahl) und y<0 (negative Zahl)
Punkte die auf den Koordinatenachsen liegen, werden keinem der vier Quadranten zugeordnet, da eine ihrer Koordinaten den Wert 0 hat
Punkte im Koordinatensystem
Du hast einen Punkt gegeben, den du eintragen möchtest oder du willst einen Punkt ablesen? Wir erklären dir jetzt, wie du das machen musst:
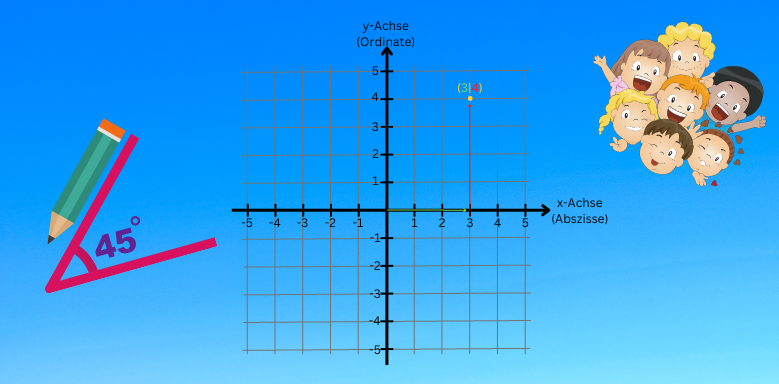
Wenn du einen Punkt P(x∣y) hast, besteht dieser aus zwei Zahlen, den Koordinaten. Die erste Koordinate bezieht sich auf den x-Achsen Wert und der zweite auf die y-Achse Koordinate. Am besten nehmen wir uns mal den Beispiel Punkt P(3∣4).
Um diesen einzuzeichnen, musst du zuerst bis zur Einheit 3 entlang der x-Achse vom Ursprung aus vorrücken. Danach musst du um 4 Einheiten nach oben, parallel zur y-Achse, verschieben. Und schon hast du die Stelle erreicht, um unseren Punkt einzuzeichnen.
Hast du bereits einen Punkt in einem Koordinatensystem eingezeichnet und möchtest dessen Koordinaten herausfinden, dann musst du einfach genau umgekehrt vorgehen.
Koordinatensystem online
Möchtest du dir einfach nur den Verlauf von einem Graphen in einem Koordinatensystem ansehen, oder gucken wo Punkte auf diesem liegen?
Dann nutz doch dieses Online-Tool. So kannst du z.B. auch gucken, wie sich durch Integrieren oder Ableiten die Lage des Graphen in dem Koordinatensystem verändert.
Koordinatensystem 3d
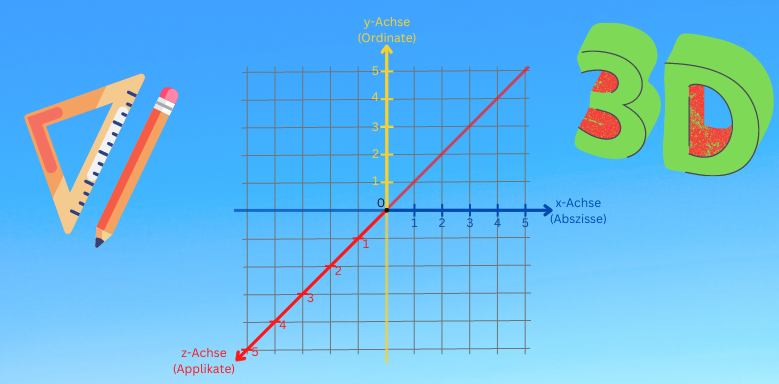
Statt zwei Achsen wie beim kartesischen Koordinatensystem gibt es jetzt drei Achsen. Zusammen stellen sie einen dreidimensionalen Raum dar.
Somit kannst du nicht nur flache Formen wie Rechtecke, sondern auch Körper, wie Würfel oder Pyramiden, darstellen.
Genau wie der Zahlenstrahl und das zweidimensionale Koordinatensystem, gibt es auch hier eine Koordinatenursprung, den Nullpunkt, an dem sich die drei Achsen schneiden.
Die dritte Achse, z-Achse, wird auch als Applikate bezeichnet und ist die räumliche Achse.
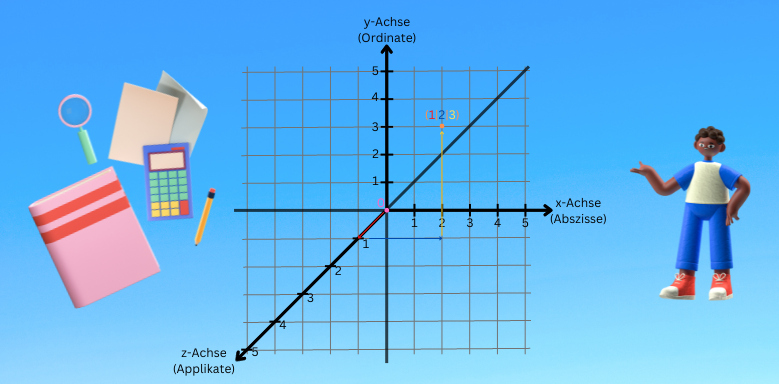
Koordinatensystem xyz zeichnen
Möchtest du selbst ein dreidimensionales Koordinatensystem erstellen ist das ganz einfach und du musst nur die folgenden Schritte beachten:
Du beginnst mit deinem 2d Koordinatensystem, wie du es bereits kennst und beschriftest die x- und y-Achse
Jetzt fehlt nur noch die 3. Achse die z-Achse. Füge diese einfach schräg von oben rechts nach unten links durch die Kästchen verlaufend ein. Aber so, dass diese auch durch den Koordinatenursprung verläuft
Nun musst du die x- und y-Achsen mit den Zahlen Einheiten (1, 2, usw.) beschriften. Am leichtesten wird dir das fallen, wenn du für eine Einheit einen Zentimeter benutzt, da das in den meisten Fällen mit den Kästchen übereinstimmt
Für die Beschriftung der z-Achse ist es am einfachsten für dich, wenn du hierfür ein schräges Kästchen als eine Einheit nimmst
Du kannst jedoch auch frei die Beschriftung aller drei Achsen wählen. Es wird dir jedoch leichter fallen, wenn alle denselben Abstand für eine Einheit haben
Punkte im dreidimensionalen Koordinatensystem
Das Vorgehen bei Punkten kannst du dir ähnlich wie beim zweidimensionalen Koordinatensystem vorstellen. Die Schreibweise der Koordinaten erfolgt in der Reihenfolge das die z-Koordinate zu erst steht und dann die x- und y-Koordinate folgt: P(z∣x∣y)
Damit du dir das ganze wieder besser vorstellen kannst, nehmen wir uns die Beispiel Koordinaten P(1∣2∣3). Bewege dich zuerst um eine Einheit vom Ursprung aus entlang der z-Achse.
Gehe danach von dort um 2 Einheiten parallel zur x-Achse. Jetzt musst du dich nur noch um 3 Einheiten nach oben parallel zur y-Achse bewegen und hast unseren Punkt erreicht.
Du musst nur umgekehrt vorgehen, wenn du die Koordinaten zu einem Punkt eintragen möchtest.