Du sollst Brüche vergleichen? Aber ist das gar nicht so einfach, weil der Nenner unterschiedlich ist oder plötzlich eine ganze Zahl vorkommt? Keine Sorge: wenn du diesen Artikel gelesen hast, kann dir kein Bruch mehr Probleme bereiten.
Es gibt einige Regeln, die man beim Vergleichen von Brüchen beachten sollte. Grundlegend geht es darum, es sich so einfach wie möglich zu machen. Wir zeigen dir einmal alle Regeln, bevor wir sie später genauer erklären.
Regeln zum Vergleichen von Brüchen
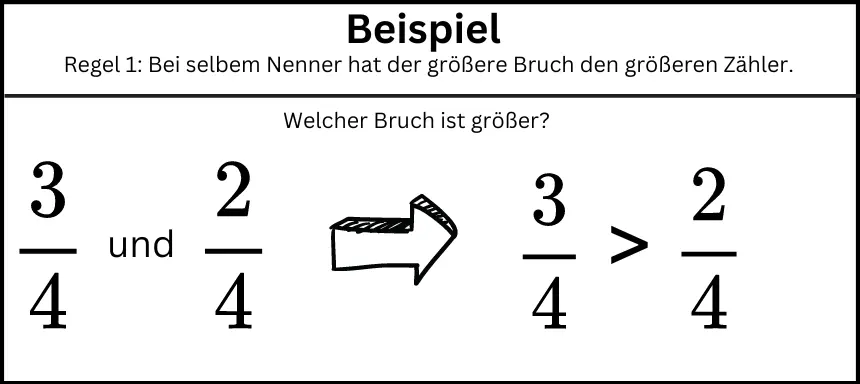
- Wenn zwei Brüche denselben Nenner haben, so hat der größere Bruch den größeren Zähler.
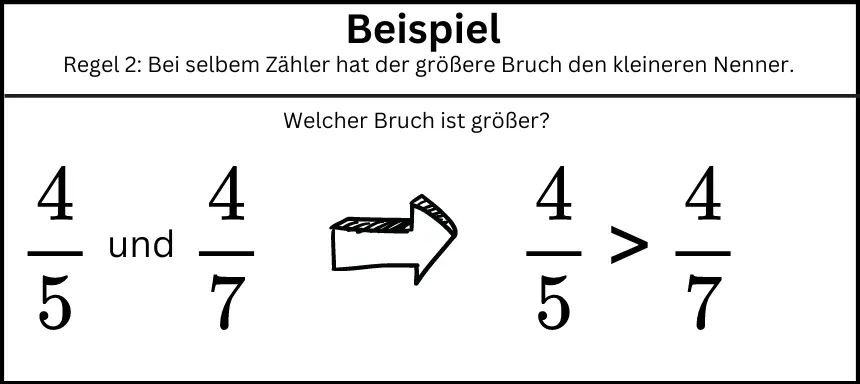
- Wenn zwei Brüche denselben Zähler haben, so hat der größere Bruch den kleineren Nenner.
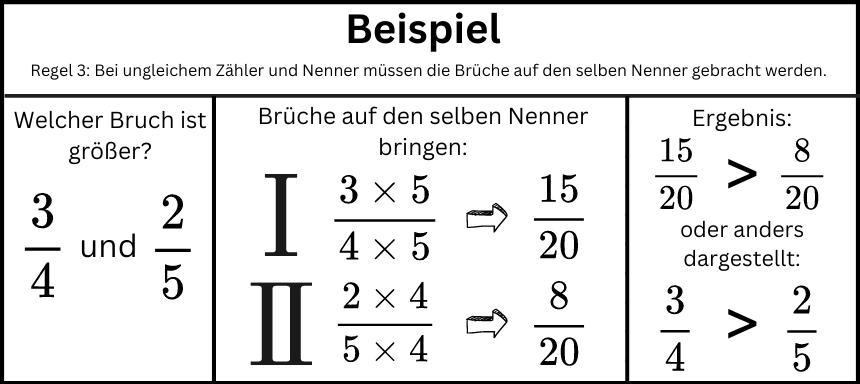
- Wenn zwei Brüche unterschiedliche Zähler und Nenner haben, so bringt man die Brüche auf einen gemeinsamen Nenner und vergleicht danach.

Gleichnamige Brüche
Gleichnamige Brüche haben den gleichen Nenner. Der größere Zähler zeigt hier den größeren Bruch an. Im Beispiel vergleichen wir also die Zähler miteinander – also 3 und 2.
Zählergleiche Brüche
Zählergleiche Brüche haben den gleichen Zähler. Der größere Nenner zeigt hier den kleineren Bruch an. Im Beispiel vergleichen wir also die Nenner – 5 und 7.
Ungleichnamige Brüche
Ungleichnamige Brüche haben weder den gleichen Zähler noch den gleichen Nenner. Du musst die Brüche daher auf einen gemeinsamen Nenner bringen. Dazu muss man einen Bruch mit dem Nenner des jeweils anderes Bruchs erweitern. Im Beispiel multiplizieren wir daher den Nenner und Zähler von ¾ mit 5 und den Nenner und Zähler von ⅖ mit 4.
Gemischte Brüche
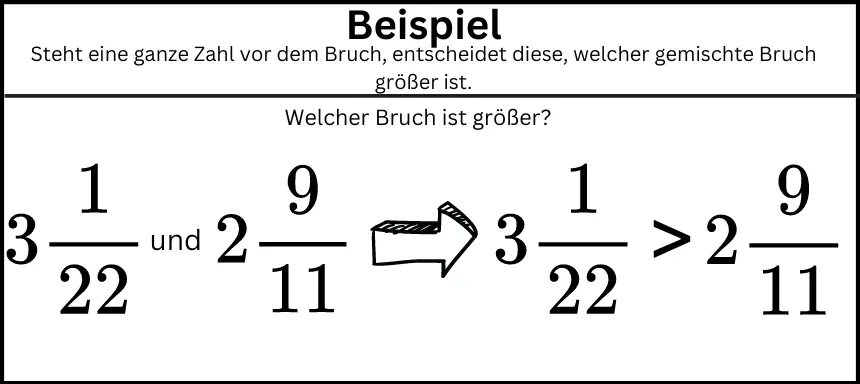
Gemischte Brüche sind Brüche, die zusätzlich eine ganze Zahl vor sich stehen haben. Dabei zeigt die größere ganze Zahl an, welcher gemischte Bruch größer ist. Sind die ganzen Zahlen gleich, dann musst du wieder die Brüche vergleichen, so wie es in den vorigen Schritten erklärt wurde.
Arbeitsblatt: Brüche vergleichen üben!
Im Folgenden haben wir 10 Aufgaben für dich, mit denen du dein Wissen testen kannst. Versuch einfach die Brüche zu vergleichen. Dann kannst du auf das “+” klicken, um die Lösung zu sehen.
2/3 und 1/3
2/3 > 1/3
3/8 und 7/8
3/8 < 7/8
1/3 und 1/4
1/3 > 1/4
3/6 und 3/5
3/6 < 3/5
2/3 und 4/5
2/3 < 4/5
5/8 und 7/13
5/8 > 7/13
2 2/3 und 3 5/7
2 2/3 < 3 5/7
4 1/2 und 5 8/16
4 1/2 < 5 8/16
1 3/4 und 1 7/19
1 3/4 > 1 7/19
2 7/8 und 2 6/9
2 7/8 > 2 6/9
FAQ
Warum vergleicht man Brüche?
- um herauszufinden welcher Bruch kleiner oder größer ist
- um Brüche ordnen zu können
Wie vergleicht man gleichnamige Brüche?
- der größere Zähler zeigt den größeren Bruch
Wie vergleicht man zählergleiche Brüche?
- der größere Nenner zeigt den kleineren Bruch
Wie vergleicht man ungleichnamige Brüche?
- die Brüche müssen auf einen gemeinsamen Nenner gebracht werden
- danach können sie verglichen werden
Wie vergleicht man gemischte Brüche?
- die ganze Zahl vor dem Bruch gibt an welcher Wert größer ist
- ist die Zahl die gleiche, müssen die Brüche wie gewohnt verglichen werden
