4,33 von 5 Sterne
Loading...
Du stehst beim Thema Asymptote total auf dem Schlauch und hast keine Ahnung, was das ist, geschweige denn wie du sie berechnen sollst? Kein Problem, wir sind hier, um dir zu helfen. In diesem Artikel lernst du…
… was eine Asymptote ist
… was es für unterschiedliche Arten gibt und
… wie du sie herausfinden kannst.
Lass uns direkt anfangen!
Asymptote Definition
Asymptoten gehören zum Thema der Kurvendiskussion in der Mathematik.
- Sie sind spezielle Geraden oder Kurven, denen sich der Graph einer Funktion unendlich nah annähert und die in manchen Fällen auch von diesem geschnitten werden.
- Man kann auch sagen, die Funktion schmiegt sich an ihre Asymptote an, wenn der x- oder y-Wert der Funktion immer weiter Richtung +∞ oder -∞ verläuft.
Was bringt die Asymptote?
Es kann sein, dass du mal eine Funktion hast, die eine Definitionslücke aufweist.
- Das heißt, es gibt ein reelles x, für das du keinen Funktionswert berechnen kannst.
- In solch einem Fall kann dieser jedoch Wert näherungsweise bestimmt werden.
- Stell dir vor, du hast die Funktion
f(x) = (x+4) / (x-6) - Für den Wert x = 6 lässt sich kein Funktionswert berechnen, da der Nenner der Funktion 6-6 = 0 werden würde und man nicht durch 0 dividieren kann.
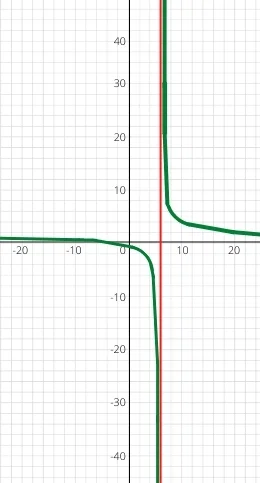
An der Stelle x = 6 hat diese Funktion deshalb eine Definitionslücke und eine senkrechte Asymptote (rot im Bild).
- Es kann auch sein, dass es einen ganzen Bereich der Funktion gibt, der nicht definiert ist.
- Zum Beispiel sind bei f(x) = √6-x alle x ≥ 6 nicht berechenbar, da nicht die Wurzel einer negativen Zahl oder von 0 gezogen werden kann.
- Die Asymptote dieser Funktion läge an der Grenze zum Definitionsbereich bei x = 6.
Kann eine Asymptote geschnitten werden?
Es wird oft gelehrt, dass dies nie passiert. Trotzdem kann es sein, dass eine Funktion ihre Asymptote einmal oder mehrfach schneidet.
- Ein Beispiel für eine Funktion, bei der das unendlich oft passiert, ist f(x) = 1+(sin(5x)/(2x)).
Hat jede Funktion ein asymptotisches Verhalten?
Nein. Eine Funktion hat eine bzw. mehrere Asymptote/n, wenn sie eine oder mehrere Funktionslücke/n aufweist. Dies kann passieren, wenn…
- … der Nenner eines Bruchs 0 wird
z.B. f(x) = 1/5-x bei x = 5 - … die Zahl unter einer Wurzel 0 oder negativ wird
z.B. f(x) = √3-x bei x ≥ 3 - … das Argument einer Logarithmusfunktion 0 oder negativ wird
z.B. f(x) = ln(4+x) bei x ≥ -4
Senkrecht, waagerecht und schief
Es gibt gerade und kurvige Asymptoten. Sind sie gerade, können sie schräg bzw. schief, waagerecht oder senkrecht sein.
- Eine Funktion kann maximal eine schräge, maximal zwei waagerechte oder unendlich viele senkrechte Asymptoten haben.
Lage: parallel zur x-Achse
Funktionsgleichung: g (x) = a (a = Konstante)
Voraussetzung: Zählergrad ≤ Nennergrad
Lage: parallel zur y-Achse
Funktionsgleichung: x = a* (a = Konstante, Polstelle)
Voraussetzung: Nenner = 0, Wurzel oder Argument einer Logarithmusfunktion ≤ 0
Lage: schräge Gerade ohne Bezugspunkt
Funktionsgleichung: g (x) = m*x+b (allgemeine Geradengleichung mit Steigung m)
Voraussetzung: Nennergrad + 1 = Zählergrad
Lage: beliebige Kurve ohne Bezugspunkt
Funktionsgleichung: keine allgemeine Funktionsgleichung
Voraussetzung: Nennergrad + a = Zählergrad a>1
Asymptote berechnen
Bei gebrochen rationalen Funktionen kannst du die unterschiedlichen Asymptoten so ermitteln:
Waagerecht: dort, wo Zählergrad ≤ Nennergrad
- Du suchst die gemeinsame höchste Potenz in Zähler und Nenner
wenn höchster Zählergrad = höchster Nennergrad
2. du dividierst den Faktor vor dieser Potenz im Zähler durch den Faktor im Nenner
Beispiel: f(x) = (4x²-3x+2) : (2x²-9)
höchste gemeinsame Potenz ist ²
-> 4:2 = 2
-> Asymptote bei y = 2
wenn höchster Zählergrad < höchster Nennergrad
2. die x-Achse ist immer die waagerechte Asymptote
Beispiel: f(x) = 5x : (x²+x)
-> Asymptote bei y=0
Senkrecht: bei jenem x, bei dem der Nenner 0 wird
- Nenner gleich Null setzen und x berechnen
Beispiel: f(x) = (7+x) : (5-x)
-> 5-x = 0 => 5 = x
-> Asymptote bei x = 5
Schief: Wenn der höchste Zählergrad um 1 höher als der höchste Nennergrad ist.
- Du suchst die höchste Potenz in Zähler und Nenner
wenn Nennergrad + 1 = Zählergrad, gibt es eine schiefe Asymptote - Zähler mithilfe einer Polynomdivision durch Nenner teilen
- Restteil (mit x im Nenner) kann gestrichen werden und übriger Teil des Ergebnisses ist die Funktionsgleichung der Asymptote
Beispiel: f(x) = (x^3+x²) : (x²-6x)
(x^3+x²) : (x²-6x) = (x+7) + (42x):(x²-6x)
-> Asymptotengleichung => f(x) = x+7
Kurvenförmig: Wenn der höchste Zählergrad um mehr als 1 höher als der höchste Nennergrad ist.
- Du suchst die höchste Potenz in Zähler und Nenner
wenn Nennergrad + a = Zählergrad (a > 1), gibt es eine kurvenförmige Asymptote - Zähler mithilfe einer Polynomdivision durch Nenner teilen
- Restteil (mit x im Nenner) kann gestrichen werden und übriger Teil des Ergebnisses ist die Funktionsgleichung der Asymptote
Beispiel: f(x) = (x3+x) : (x-6)
(x3+x) : (x-6) = x2+6x+37 + (222):(x-6)
-> Asymptotengleichung => f(x) = x2+6x+37
Du brauchst noch ein bisschen Hilfe bei den Potenzen? Wir haben da den perfekten Artikel für dich.
Asymptotisches Verhalten der
e-Funktion
Die normale e-Funktion lautet:
f(x) = e^x (e hoch x)
- Sie hat eine waagerechte Asymptote bei y = 0, also genau auf der x-Achse.
- Deshalb nähert sich die Funktion der x-Achse an, wenn die x-Werte immer kleiner werden.
- Wird die e-Funktion um eine bestimmte Strecke in Richtung der y-Achse verschoben, verschiebt sich auch die Asymptote um diese Strecke und folgt sozusagen der Funktion.
- Eine Verschiebung auf der x-Achse ändert jedoch nichts.
Übungen mit Lösung
Nenner gleich Null setzen und x ausrechnen:
x-6 = 0
x = 6
-> senkrechte Asymptote bei x = 6
Mit Polynomdivision Zähler durch Nenner teilen und Rest streichen:
(8+x²) : x = x+(8/x)
–> schiefe Asymptote bei g(x) = x
Höchste gemeinsame Potenz ist ².
3:2 = 1,5
–> Waagrechte Asymptote bei g(x) = y = 1,5
Mit Polynomdivision Zähler durch Nenner teilen und Rest streichen:
(10x³+6) : (5x) = 2x²+(6):(5x)
–> kurvenförmige Asymptote bei g(x) = 2x²
Hol dir unsere Mathe Hilfe jetzt nach Hause! Das Nachhilfe-Team hält zahlreiche erfahrene Tutoren bereit, die dir Mathematik sowohl Zuhause als auch Online– unser am meisten gewähltes Programm- beibringen möchten!
Kennst du außerdem schon unsere weiteren Ratgeber für das Fach Mathematik? Hier findest du zum Beispiel alles zum berechnen von Diagonalen und Schnittpunkten.
