3,81 von 5 Sterne
Loading...
Die Umkehrfunktion spielt besonders bei der Berechnung einer Aufgabe in einem Kontext eine große Rolle. Wenn du zum Beispiel eine Funktion gegeben hast, die dir den Zusammenhang zwischen Zeit (x) und Bevölkerungszahl (y) angibt, du aber herausfinden möchtest, zu welcher Zeit die Bevölkerungszahl bei einer bestimmten Zahl ist, musst du die Umkehrfunktion bilden.
Wir zeigen dir Schritt für Schritt anhand von Beispielen, wie du eine Umkehrfunktion richtig bildest und worauf du dabei ganz besonders achten musst.
Eine Umkehrfunktion ordnet, wie der Name schon sagt die Variablen x und y umgekehrt zu. Eine Funktion kann nur umgekehrt werden, wenn jedem x-Wert höchstens ein y-Wert zugeordnet wird.
Das heißt, dass x und y-Werte vertauscht werden.
Eine Umkehrfunktion wird durch f-1(x) gekennzeichnet.
Im Allgemeinen wird eine Umkehrfunktion gebildet, indem die Funktion an der Winkelhalbierenden gespiegelt wird. Was das genau bedeutet schauen wir uns jetzt im Detail an.
Die Winkelhalbierende ist eine Funktion der Form g(x) = x.
Diese wird als Spiegelachse genutzt, um die Umkehrfunktion zu bilden. Damit wir aber nicht jeden einzelnen Punkt der Funktion händisch spiegeln müssen, zeigen wir dir wie du die Umkehrfunktion einfach berechnen kannst.
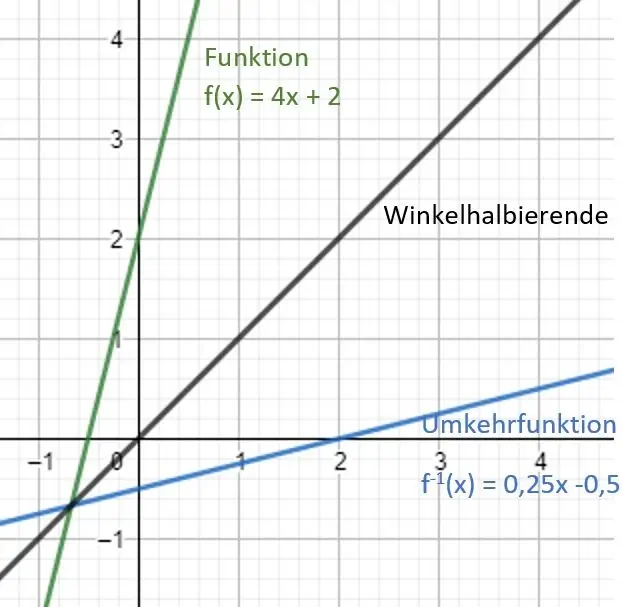
Umkehrfunktion bestimmen anhand eines Beispiels
Die zwei Schritte:
- Funktion nach x auflösen
- die Variablen x und y vertauschen
Schauen wir uns dazu folgende lineare Funktion an:
f(x) = y = 5x + 3
Bei dieser Funktion wird jedem y-Wert genau ein x Wert zugeordnet. Deshalb lässt sich die Funktion umkehren.
1. Funktion nach x auflösen
y = 5x + 3 |-3
y – 3 = 5x |:5
⅕ y – ⅗ = x
2. x und y tauschen
⅕ x – ⅗ = y
Damit ergibt sich die Umkehrfunktion f-1(x) = ⅕ x – ⅗
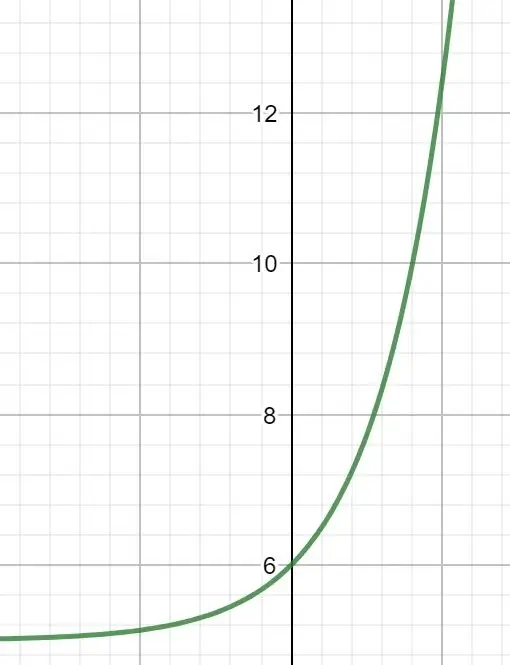
Umkehrfunktion Exponentialfunktion
Die natürliche Exponentialfunktion ist dadurch gekennzeichnet, dass sie sich bei einer Ableitung nicht verändert. Bei einer Umkehrung der Funktion verändert sie sich allerdings.
Die Umkehrfunktion der Exponentialfunktion f (x) = ex ist die natürliche Logarithmusfunktion f-1(x) = ln(x).
Schauen wir uns als Beispiel die Funktion f (x) = y = ex + 5 an.
1. Funktion nach x auflösen
y = ex + 5 | -5
y -5 = ex | ln()
ln(y – 5) = x
2. x und y tauschen
f-1 (x) = y = ln(x – 5)
Damit ergibt sich die Umkehrfunktion f-1(x) = ln(x – 5)
Umkehrfunktion trigonometrische Funktionen
Zu den trigonometrischen Funktionen gehören Sinus, Cosinus und Tangens. Auch diese lassen sich Umkehren.
Umkehrfunktion Sinus
Die Sinusfunktion ist genau wie auch alle anderen trigonometrischen Funktionen periodisch. Das bedeutet, dass sich der Verlauf des Graphen in einem bestimmten Abstand immer wiederholt. Eine Sinusfunktion sieht wie folgt aus:
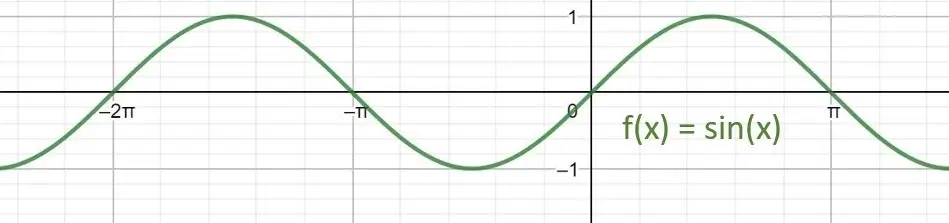
Schauen wir uns ein Beispiel dazu an, wie wir die Umkehrfunktion bilden können.
f(x) = y = sin (2x – 4)
Wie bei der Berechnung aller Umkehrfunktionen müssen wir zwei Schritte durchführen:
- Funktion nach x auflösen
- die Variablen x und y vertauschen
Das Problem dabei ist, dass unser x in der Sinusfunktion steht und wir diese somit nicht durch die 4 Grundrechenarten auf eine Seite bekommen. Um das x aus der Sinusfunktion zu bekommen, müssen wir sin-1 (auch arcsin oder asin genannt) verwenden.
1. Schritt: Funktion nach x auflösen
y = sin (2x – 4) | sin-1
sin-1(y) = 2x – 4 |+4
sin-1(y) + 4 = 2x |:2
0,5 sin-1(y) + 2 = x
2. Schritt: die Variablen x und y vertauschen
0,5 sin-1(x) + 2 = y = f-1(x)
Aber wieso können wir unsere Funktion Problemlos mit sin-1 multiplizieren?
Dazu verwenden wir ein Potenzgesetz.
Dieser besagt, dass bei einer Multiplikation zweier Potenzen mit der gleichen Basis die Exponenten addiert werden.
an ⋅ am = an+m
Auf die Sinusfunktion angewandt:
sin(x) * sin-1 (x) = sin1-1 (x) = sin0(x) = 1x
Im letzten Schritt haben wir wieder ein Potenzgesetz verwendet. Diese besagt, dass Jede Basis mit dem Exponenten 0 gleich 1 ist.
a0 = 1
Umkehrfunktion Cosinus
Bei der Berechnung der Umkehrfunktion der Cosinus Funktion gehen wir genauso vor, wie bei der Berechnung der Umkehrfunktion der Sinusfunktion. Schauen wir uns zuerst an, wie die Sinusfunktion aussieht.
Um die Umkehrfunktion zu berechnen, müssen wir nun nicht sin-1 verwenden, sondern cos-1. Die sonstige Berechnung bleibt aber identisch.
Schauen wir uns dazu dieses Beispiel an:
f(x) = cos (x + 2)
1. Schritt: Funktion nach x auflösen
y = cos (x + 2) | cos-1
cos-1(y) = x + 2 |-2
cos-1(y) – 2 = x
2. Schritt: die Variablen x und y vertauschen
cos-1(x) + 2 = y = f-1(x)
Umkehrfunktion Aufgaben
Hier findest du Aufgaben, um zu überprüfen, ob du verstanden hast, wie eine Umkehrfunktion gebildet wird.
Bilde die Umkehrfunktion f-1(x) der Funktion:
f(x) = 2x + 4
1. Schritt: Funktion nach x auflösen
f(x) = y = 2x + 4
y = 2x + 4 | -4
y -4 = 2x |:2
0,5y – 2 = x
2. Schritt: die Variablen x und y vertauschen
0,5y – 2 = x
0,5x – 2 = y = f-1 (x)
Die Umkehrfunktion lautet f-1 (x) = 0,5x – 2
Bilde die Umkehrfunktion f-1(x) der ganzrationalen Funktion:
f(x) = x2 + 2
1. Schritt
f(x) = y = x2 + 2
y = x2 + 2 | -2
y – 2 = x2 | Wurzel ziehen
= x
2. Schritt: die Variablen x und y vertauschen
= y
Die Umkehrfunktion lautet f-1(x) =
Bilde die Umkehrfunktion f-1(x) der Funktion:
f(x) = x3
1. Schritt: Funktion nach x auflösen
f(x) = y = x3
y = x3 |3. Wurzel ziehen
= x
2. Schritt: die Variablen x und y vertauschen
= y
Die Umkehrfunktion lautet f-1(x) =
FAQ zu Umkehrunktion bilden
Wann ist eine Funktion umkehrbar?
Eine Funktion besitzt eine Umkehrfunktion, wenn jedem x Wert genau ein y Wert zugeordnet wird und auch andersherum. Ist dies nicht der Fall, muss bei der Bestimmung der Umkehrfunktion ein Definitionsbereich festgelegt werden, auf den dieses Kriterium zutrifft.
Wofür brauche ich eine Umkehrfunktion?
Eine Umkehrfunktion brauchst du, wenn du zu einem bestimmten y Wert den zugehörigen x Wert herausfinden möchtest.
Wie berechnet man die Umkehrfunktion?
Zur Berechnung einer Umkehrfunktion müssen wir immer zwei Schritte durchführen:
- Funktion nach x auflösen
- die Variablen x und y vertauschen
Du findest weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.
Artikel hat mir geholfen, danke schön!!
Aber schaut mal bitte:
es müsste doch -2 heißen! bei der folgenden Aufgabe:
1. Schritt: Funktion nach x auflösen
y = cos (x + 2) | cos-1
cos-1(y) = x + 2 |+2
cos-1(y) + 2 = x
Vielen Dank, wurde korrigiert 🙂
“Dieser besagt, dass bei einer Multiplikation zweier Potenzen mit der gleichen Basis die Exponenten addiert werden.
a^n + a^m = a^(n+m)”
Hier hat sich leider ein Fehler eingeschlichen:
Der Text ist richtig, aber die Formel nicht! Auf der linken Seite müsste eine Multiplikation sein.
Wurde korrigiert, vielen Dank!