4,50 von 5 Sterne
Loading...
Symmetrie spielt in der Geometrie eine wichtige Rolle. Dieser Artikel gibt einen kleinen Überblick über die 4 häufigsten Arten der Symmetrie. Wann etwas symmetrisch ist und worin die Unterschiede in den Symmetrien liegen, erfährst du im Folgenden.
Symmetrie kann in 2 Fällen auftreten.
- Ein geometrisches Gebilde kann in sich eine Symmetrie aufweisen.
- Zwei geometrische Gebilde können zueinander eine Symmetrie aufweisen.
Hier ein Beispiel:
Wenn man das Dreieck in der Mitte faltet, passen alle Seiten perfekt aufeinander. Damit ist das Dreieck in sich Achsensymmetrisch.
Klappt man das linke Dreieck entlang der Spiegelachse auf die rechte Seite, dann liegt das linke Dreieck exakt auf dem rechten Dreieck. Damit sind die beiden Dreiecke zueinander achsensymmetrisch
Achsensymmetrie – die bekannteste Symmetrie
Bei der Achsensymmetrie spiegelt man ein geometrisches Gebilde an einer festgelegten Achse (Spiegelachse).
Dabei überträgt man alle Punkte einer Figur mit den selben Abständen zur Spiegelachse auf die gegenüber liegende Seite der Achse.
Hier ein Beispiel:
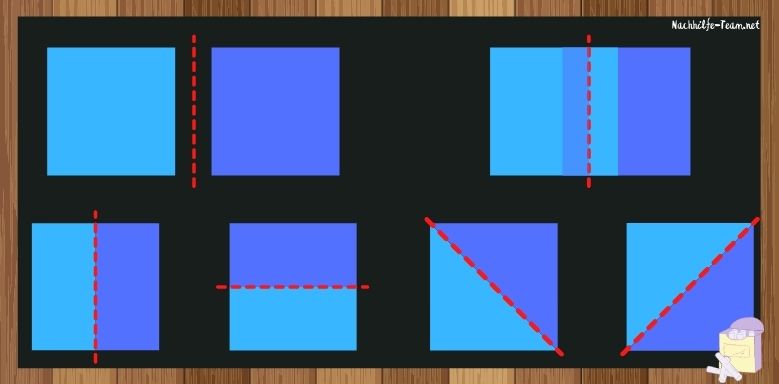
Das Bild zeigt Möglichkeiten, wie Achsensymmetrie in beiden Fällen bei einem Quadrat vorkommen kann.
Du erlebst die Achsensymmetrie täglich, wenn du in den Spiegel schaust.
Der Spiegel ist hierbei die Spiegelachse und spiegelt alles in gleichen Maßen und Abständen im Spiegelbild.
Punktsymmetrie
Bei der Punktsymmetrie gibt es keine Achse, an der Gespiegelt wird.
Wie der Name schon verrät, spiegelt man ein geometrisches Gebilde an nur einem einzigen Punkt.
Dabei überträgt man alle Punkte einer Figur, mit den selben Abständen zum Spiegelpunkt, auf die gegenüberliegende Seite des Spiegelpunktes.
Hier ein Beispiel:
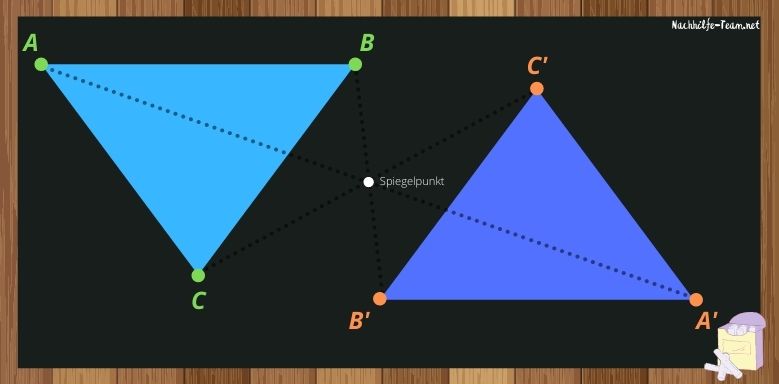
Die beiden Dreiecke sind Punktsymmetrisch zueinander. Alle gespiegelten Eckpunkte haben den gleichen Abstand zum Spiegelpunkt, wie der jeweilige Ursprungspunkt.
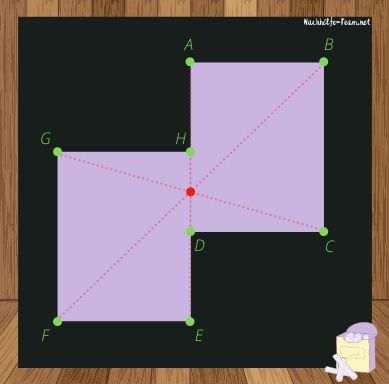
Diese Figur ist in sich Punktsymmetrisch. Alle Eckpunkte lassen sich am Spiegelpunkt spiegeln. Somit ist die Figur nach der Spiegelung auf sich selbst abgebildet.
Drehsymmetrie – die seltenste Symmetrie
Bei der Drehsymmetrie gibt es wie bei der Punktsymmetrie einen Spiegelpunkt.
Um diesen Punkt dreht man ein geometrisches Gebilde um eine bestimmte Gradzahl. Dabei verändern sich alle Punkte einer Figur um die selbe Gradzahl
Hier ein Beispiel:
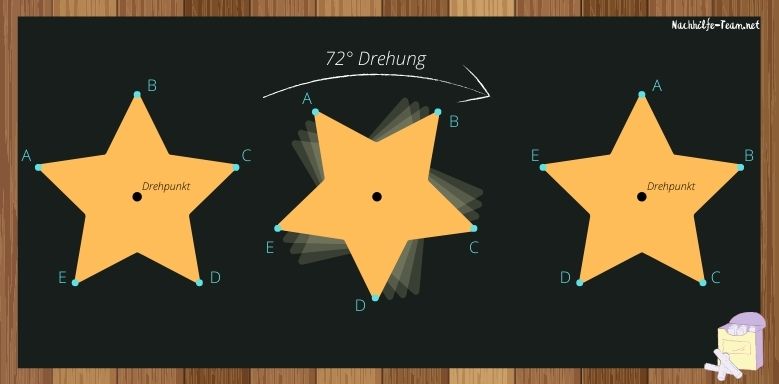
Der Stern ist nach einer Drehung von 72 Grad um den Drehpunkt drehsymmetrisch, da er nach der Drehung genau auf sich selbst abgebildet ist.
Hinweis: Wird bei der drehsymmetrie eine Figur um 180° gedreht, so erhält man eine Punktsymmetrie. Somit ist die Punktsymmetrie eine Form der Drehsymmetrie.
Asymmetrie
Bei der Asymmetrie liegt die Symmetrie in keiner der 3 Formen vor. Dies kann sowohl für eine Figur an sich, als auch für 2 verschiedene Figuren gelten.
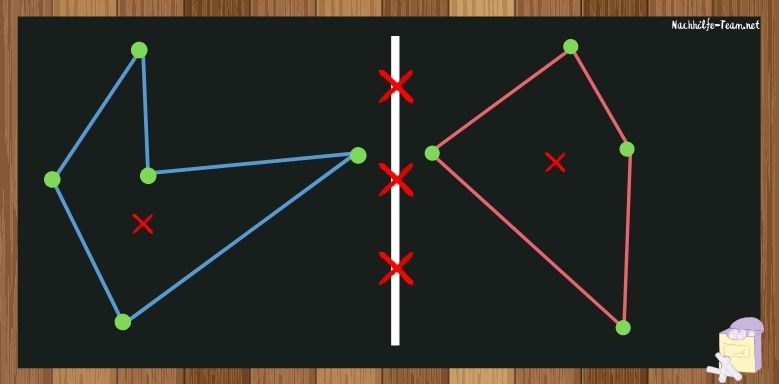
Die Figuren im Bild haben keinerlei Symmetrieeigenschaften an sich. Sie sind weder in sich, noch zueinander Achsen-, Punkt- oder Drehsymmetrisch. Daher spricht man hier von Asymmetrie.
Empfohlene Videos
Achsensymmetrie
Punktsymmetrie
Hat dir unsere Seite gefallen? Wenn wir dir weiterhelfen konnten, würden wir uns über einen Kommentar von dir sehr freuen 🙂
Wenn du noch etwas über andere Mathethemen erfahren willst, lernst du hier wie man Gewichte umrechnet, Flächeninhalte berechnet oder wie Bruchrechnen funktioniert.
Hast du es vielleicht allgemein nicht so mit den Zahlen? Dann wäre Mathe Nachhilfe sehr wahrscheinlich genau das Richtige für dich.
Hier kannst du ganz einfach mit der Mathe Nachhilfe oder der Online Mathe Nachhilfe anfangen.
Wenn du dich vorher noch mehr über das Thema informieren möchtest, findest du hier alle Infos zu unseren Nachhilfe-Leistungen.
Mein Sohn hat aktuell in Mathe das Thema Symmetrie und ich versuche es ihm leicht zu erklären. Die Erklärung finde ich wirklich gut, da mit den Bildern noch ein guter Bezug zur Erklärung entsteht und ich es ihm so deutlich machen kann, vielen Dank dafür. Ich habe nämlich gar nicht bedacht, dass nicht nur eine Forma an sich symmetrisch sein kann, sondern auch zu einer zweiten. Nun kann ich meinem Sohn selbst Mathe Nachhilfe geben.
Supergut erklärt ich hab alles sofort kapiert