4,14 von 5 Sterne
Loading...
Diagonalen begegnen uns oft im Alltag. Bei Fernsehern und Laptops wird die Bildschirmdiagonale immer angegeben. Aber was genau ist eine Diagonale und wie kann ich eine Diagonale berechnen? In diesem Artikel erklären wir dir…
… was eine Diagonale ist
… wie du Diagonalen an verschiedenen Formen und Körpern berechnest
… und was du mit Diagonalen im Alltag anfängst.
Am Ende des Artikels haben wir noch ein paar Übungsaufgaben für dich zu diesem Thema bereitgestellt.
Diagonale – kurze Definition
Der Begriff Diagonale gehört in der Mathematik zum Feld der Geometrie und wird meistens mit “d” angegeben.
Eine Diagonale ist die kürzeste Strecke zwischen zwei Ecken von zweidimensionalen Formen oder dreidimensionalen Körpern.
Bei dieser Verbindung der Ecken ist die Diagonale weder eine Seite noch eine Kante einer Figur, sondern führt sozusagen durch die Form oder den Körper hindurch. Das heißt eine Diagonale ist die Verbindung von zwei Punkten, die noch nicht miteinander verbunden sind.
Diagonale berechnen – wie mache ich das?
Wie du eine Diagonale berechnest, kommt auf den vorliegenden Körper an. Man kann es also nicht pauschal sagen. Im Verlauf dieses Artikels erklären wir bei vielen verschiedenen Körpern, wie du die Diagonalen berechnen kannst.
Was bedeutet die Diagonalen stehen senkrecht zueinander?
Stehen zwei Diagonalen senkrecht zueinander, ist der Winkel zwischen ihnen exakt 90°, also rechtwinklig.
Du willst zum wahren Mathe Experten werden? Wir haben einen idealen Tutor für deine Mathe Nachhilfe! Egal ob Zuhause oder Online.
Unsere erfahrenen Studentenlehrer stehen dir zur Seite.
Schau doch mal vorbei!
Verbindungsstrecke bei Rechteck bestimmen
Die Diagonalen bei einem Rechteck lassen sich ganz einfach mit dem Satz des Pythagoras herleiten. Ein Rechteck besteht aus zwei rechtwinkligen identischen Dreiecken und hat jeweils zwei gegenüberliegende gleich lange Seiten.
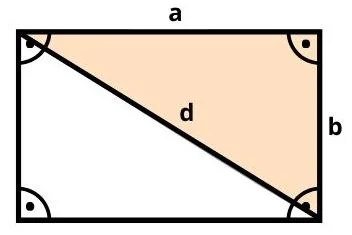
Du musst jetzt also nur die lange Seite (Hypotenuse) des Dreiecks ausrechnen. Denn diese Seite ist die Diagonale des Rechtecks. Der Satz des Pythagoras besagt: a² + b² = c². Also Länge des Rechtecks² • Breite des Rechtecks² = Diagonale².
Wir erinnern uns: Die Diagonale wird immer mit “d” angegeben. In diesem Fall ist sie das gleiche wie “c”.
Nehmen wir an, das Rechteck hat eine Fläche von 4cmx3cm. Damit sind auch die Katheten des Dreiecks 4cm und 3cm lang. Setzen wir diese Werte in den Satz des Pythagoras ein, erhalten wir 4²+3² = c².
Damit wir nur d, also die Diagonale erhalten, müssen wir nun die Wurzel der gesamten Gleichung ziehen.
√4²+3² = d
√16+9 = d
√25 = c
5 = d
Wir erhalten das Ergebnis d = 5 also ist die Hypotenuse der beiden Dreiecke im Rechteck sowie die Diagonale des Rechtecks 5cm lang.
Durch diese Herleitung bekommen wir auch die allgemeine Formel für die Diagonale (d) im Rechteck mit den Seitenlängen a und b: √a²+b² = d
Sind bei einem Rechteck die Diagonalen gleich lang?
Ja, bei einem Rechteck sind die beiden Diagonalen immer gleich lang. Außerdem halbieren sie sich jeweils. Es ist egal, wie du ein Rechteck in zwei Dreiecke aufteilst, die Hypotenusen und damit die Diagonalen des Rechtecks sind immer gleich lang.
Beachte, dass die einzelnen Teile der Formeln immer in der gleichen Maßeinheit z.B. cm angegeben sind. Hast du a in Metern und b in cm, musst du erst eins davon an das andere anpassen und die Längeneinheiten umrechnen. Die Diagonale d ist dann auch in dieser Einheit.
Diagonale beim Quadrat
Ein Quadrat ist eine spezielle Form eines Rechtecks. Auch bei einem Quadrat sind die vier Ecke rechtwinklig, jedoch sind hier alle vier Seiten gleich lang.
Da sich Rechteck und Quadrat so ähnlich sind, ist auch die Berechnung der Diagonale fast gleich.
Wie rechnet man die Verbindungslinien eines Quadrats aus?
Beim Quadrat teilt die Diagonale die Form ebenfalls in zwei identische rechtwinklige Dreiecke.
Auch hier nehmen wir wieder den Satz des Pythagoras zu Hilfe: a² + b² = d². Da beim Quadrat alle Seiten gleich lang sind, wird die Formel zu a² + a² = d² → 2•a² = d².
Lösen wir die Formel jetzt nach d auf, erhalten wir:
√2•a² = d
√2•√a² = d
√2 • a =d
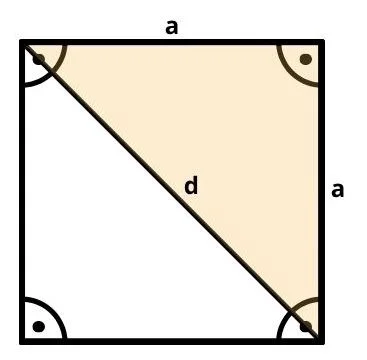
Und damit haben wir die allgemeine Formel für die Diagonale im Quadrat: √2•a =d
Haben wir ein Quadrat mit der Seitenlänge von 6cm ergibt sich daraus: √2•6 = d
Rechnen wir das jetzt aus, bekommen wir d = 8,49cm. Die Diagonale von unserem Quadrat ist also 8,49cm lang.
√2 ist ungefähr 1.414
Die Schrägen einer Raute
Eine Raute wird auch Rhombus, Karo oder, weil sie wie ein Drache aussieht, auch Drachenviereck genannt.
Ein Rhombus besteht aus vier gleichlangen Seiten a, bei denen die gegenüberliegenden zwei parallel zueinander sind. Die gegenüberliegenden Winkel haben die gleiche Größe.
Die zwei Diagonalen einer Raute verbinden jeweils diese Winkel miteinander, halbieren sich gegenseitig und haben unterschiedliche Längen. Außerdem stehen die Diagonalen rechtwinklig zueinander.
Eine Raute sieht aus wie ein schiefes Quadrat und ist eine Untergruppe der Parallelogramme. Was ein Parallelogramm ist, erklären wir weiter unten.
Diagonale berechnen beim Rhombus – wie geht das?
Du kannst jedes Viereck in zwei Dreiecke zerteilen. Bei einem Rhombus sind diese jedoch nicht rechtwinklig. Bei diesen Dreiecken kannst du deshalb auch nicht den Satz des Pythagoras anwenden.
Wenn du diese zwei Dreiecke jedoch ein weiteres mal halbierst, sodass die Raute in vier Dreiecke zerlegt ist, sind die Dreiecke rechtwinklig.
Da die zwei Diagonalen unterschiedlich lang sind, müssen wir auch zwei verschiedene Formeln herleiten. Die längere Diagonale heißt e und die kürzere f.
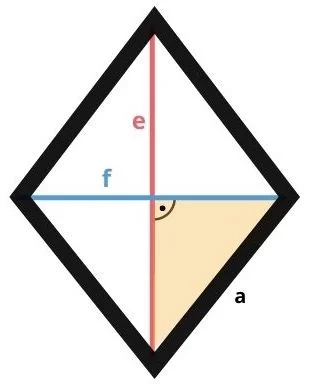
Nimmst du nun eins der vier Dreiecke in der Raute, siehst du, dass die Katheten jeweils halb so lang wie e und f sind.
Wenden wir nun des Satz des Pythagoras für dieses Dreieck an, erhalten wir:
(e/2)² + (f/2)² = a²
Nun müssen wir diese Formel nach e auflösen:
(e/2)² + (f/2)² = a²
(e/2)² = a² – (f/2)²
e/2 = √a²-(f/2)²
e = 2•√a²-(f/2)²
Wir erhalten: e = 2•√a²-(f/2)² und wenn wir nach f auflösen: f = 2•√a²-(e/2)²
Du brauchst immer die Länge der Seiten und einer Diagonale, um die zweite Diagonale auszurechnen.
Beispiel:
Die Seiten der Raute sind 17cm lang. Die Länge der Diagonale f beträgt 16cm.
a = 17cm, f = 16cm, e = ?
e = 2•√17²-(16/2)²
e = 2•√17²-8²
e = 2•√289-64
e = 2•√225
e = 2•15
e = 30
Ergebnis: e = 30cm
Diagonalen im Parallelogramm ausrechnen
Ein Parallelogramm ist eine Form mit vier Seiten, bei denen jeweils zwei parallel zueinander stehen. Bei einem Parallelogramm sind im Vergleich zu einer Raute nicht alle vier Seiten gleich lang, sondern jeweils nur die zwei gegenüberliegenden.
Auch hier heißen die Diagonalen e und f. Wenn du dir das Parallelogramm genau ansiehst, erkennst du, dass du auf der einen Seite ein kleines Dreieck “abschneiden” kannst und so ein rechtwinkliges Dreieck im Parallelogramm erhältst.
Berechnung von f
Wie du in der Grafik siehst, haben wir nun eine kleine Strecke m, deren Länge wir brauchen, um die Diagonale zu bestimmen. Um m rauszufinden, können wir bei dem kleinen Dreieck, das wir abgeschnitten haben, den Satz des Pythagoras anwenden:
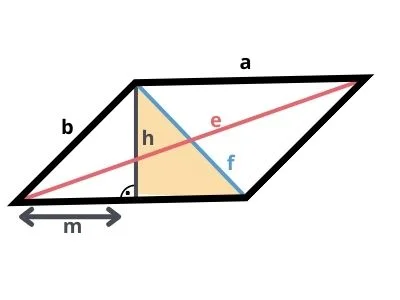
(kurze Seite des Parallelogramms b)² = m²+(Höhe des Parallelogramms ha)²
Lösen wir dies nach m auf, erhalten wir:
b²-h² = m²
√b²-h² = m
Haben wir m ermittelt, können wir mit der Strecke a-m und dem Satz des Pythagoras die Hypotenuse des markierten rechtwinkligen Dreiecks im Parallelogramm ausrechnen. Diese ist gleichzeitig die kürzere Diagonale f.
f² = (a-m)²+h²
f = √(a-m)²+h²
Damit haben wir die eine Diagonale des Parallelogramms ermittelt.
Berechnung von e
Für die zweite Diagonale e schieben wir einfach das kleine Dreieck, das wir auf der einen Seite abgeschnitten haben, umgedreht auf die andere Seite und “kleben” es an das Parallelogramm.
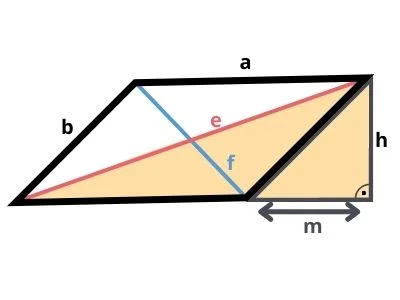
Auch hier entsteht nun ein rechtwinkliges Dreieck, dessen Hypotenuse die Diagonale e ist. Um die Hypotenuse zu bestimmen rechnen wir mit dem Satz des Pythagoras:
e² = (a+m)²+h²
e = √(a+m)²+h²
So einfach ist die Berechnung der zweiten und längeren Diagonalen des Parallelogramms.
Beispiel:
Die lange Seite des Parallelogramms ist 10cm lang und die kurze 7cm. Die Höhe beträgt 5cm.
Wie lang sind die beiden Diagonalen?
a = 10cm, b = 7cm, h = 5cm, f = ?, e = ?
m = √b²-h²
einsetzen ergibt:
m = √7²-5²
m = √49-25
m = √24
m = 4,9
f = √(a-m)²+h²
einsetzen ergibt:
f = √(10-4,9)²+5²
f = √5,1²+5²
f = √26,01+25
f = √51,01
f = 7,14
e = √(a+m)²+h²
einsetzen ergibt:
e = √(10+4,9)²+5²
e = √14,9²+5²
e = √222+25
e = √247
e = 15,7
Ergebnis: f = 7,14cm, e = 15,7cm
Welche Eigenschaft besitzen die Schrägen der Parallelogramme?
- Diagonalen sind nicht gleich lang
- Diagonalen halbieren sich gegenseitig
- Diagonalen teilen das Parallelogramm in insgesamt vier Dreiecke
Hat ein Dreieck auch Verbindungslinien?
Wir haben oben erklärt, dass eine Diagonale immer zwei Ecke verbindet, die nicht durch andere Strecken miteinander verbunden sind. Bei einem Dreieck sind jedoch bereits alle drei Ecken mit den anderen beiden verbunden.
Deshalb hat ein Dreieck auch keine Diagonalen.
Raumdiagonalen beim Quader – jetzt dreidimensional
Ein Quader ist im Gegensatz zu den oben besprochenen flachen Formen ein dreidimensionaler Körper. Das heißt, er hat eine Länge a, Breite b und Höhe h und besteht aus sechs Seiten, von denen jeweils die gegenüberliegenden zwei identisch sind.
Die vier sogenannten Raumdiagonalen führen durch den Quader hindurch und verbinden immer zwei Ecken miteinander.
Diagonale berechnen in 3D
Da alle Ecken eines Quaders rechtwinklig sind, kannst du zur Berechnung der Raumdiagonalen D wieder den Satz des Pythagoras anwenden. Da hier alle Diagonalen gleich lang sind, reicht es, wenn du eine davon ausrechnest.
Stell dir vor, dass im Quader ein aufrechtes rechtwinkliges Dreieck steht. Von diesem möchtest du nun die Hypotenuse, also die längste Seite ermitteln, denn diese ist die Raumdiagonale des Quaders.
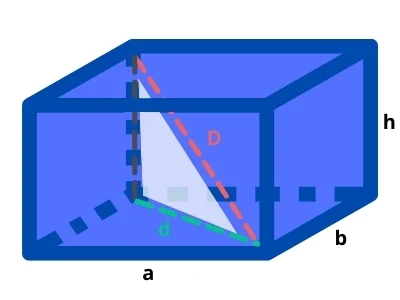
Die beiden Katheten des Dreiecks sind die Höhe des Quaders und die Diagonale der Grundfläche. Die Grundfläche ist, wie jede Seite des Quaders, ein Rechteck. Und wie du hier die Diagonale berechnest, hast du ja oben bereits gelernt.
d² = a² + b²
d = √a²+b²
d = Diagonale der Grundfläche
Nun können wir ganz einfach die Hypotenuse des aufrecht stehenden Dreiecks ausrechnen:
D² = a² + b² + h²
D = √a² + b² + h²
D = Raumdiagonale des Quaders
Beispiel:
a = 6cm, b = 4cm, h = 5cm, D = ?
D = √a² + b² + h²
einsetzen ergibt:
D = √6cm²+4cm²+5cm² = 8,77cm
Ergebnis: D = 8,77cm
Wie viele Diagonalen hat ein Quader?
Ein Quader hat vier Raumdiagonalen, die jeweils zwei Eckpunkte innerhalb des Körpers miteinander verbinden. Die Raumdiagonalen sind alle gleich lang.
Mathematik im Alltag: Die Fernseher-Diagonale
Ein häufiges Beispiel von Diagonalen findest du bei Fernsehern und anderen elektronischen Geräten wie Laptops. Die Bildschirmgrößen werden meistens durch ihre Diagonale angegeben.
So braucht man nämlich nur eine Zahl. Würde man die Größe über die Länge und Breite angeben, müsste man immer zwei Zahlen benennen.
Wie wird die Diagonale beim Fernseher gemessen?
Da Fernseher gemeinhin rechteckig sind, kannst du hier die Formel für Rechtecke anwenden, die wir oben ermittelt haben: √a²+b² = d
Ist der Fernseher 90cm • 50cm groß, beträgt die Diagonale also √90²+50² = 103cm ≈ 40 Zoll.
Diagonale beim Fernseher – was bedeutet das?
Die Diagonale beim Fernseher oder bei anderen Bildschirmen sagt aus, wie weit zwei Ecken voneinander entfernt sind, die nicht durch Kanten verbunden sind. Also von links unten nach rechts oben oder von links oben nach rechts unten.
Je länger die Diagonale ist desto größer ist der Bildschirm, ohne dass sich das Verhältnis von Länge und Breite verändert.
Wie groß ist ein 55 Zoll Fernseher in cm?
Zoll, im englischen Sprachraum auch Inch genannt, ist eine Maßeinheit , die oft für Bildschirmdiagonalen verwendet wird. 1 Zoll entspricht 2,54cm. Das heißt ein 55 Zoll Fernseher hat eine Bildschirmdiagonale von 139,7cm.
Zum Abschluss haben wir hier noch eine Übersicht mit allen Formeln für die Diagonalen der verschiedenen Körper.
Hier gibt’s die Übersicht auch als Download.
Diagonale berechnen – Übungen mit Lösungen
Wenn du willst, kannst du dein Wissen sofort mit unseren Übungsaufgaben testen.
In den Aufgaben werden dir die Körper und verschiedene Längen gegeben. Deine Aufgabe ist es, die Diagonale zu berechnen. Klick einfach auf eine Aufgabe, um dir die Lösung anzuzeigen.
d = √15cm²+9cm² = 17,5cm
e = 2•√4cm²-(3cm/2)² = 7,4cm
D = √10cm²+4cm²+7cm² = 12,8cm
d = √2 • 12cm = 16,97cm
m = √7²-5² = 4,9cm
f = √(8cm-4,9cm)²+5cm² = 5,9cm
