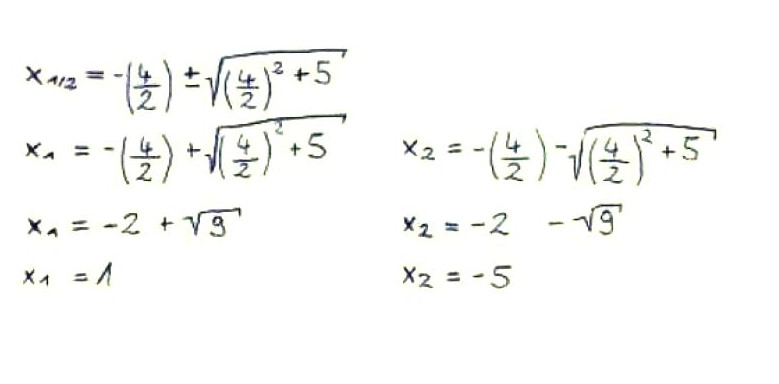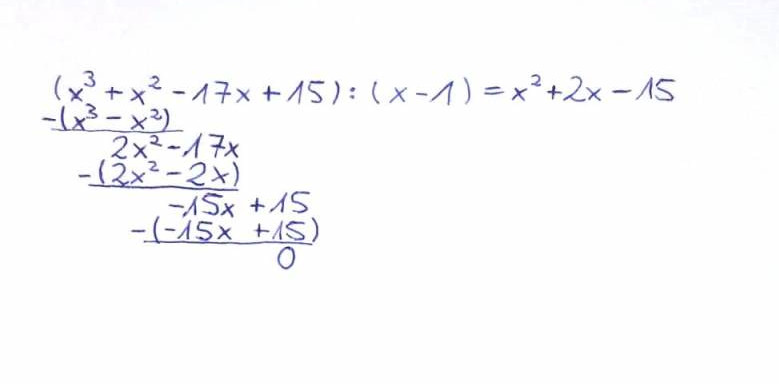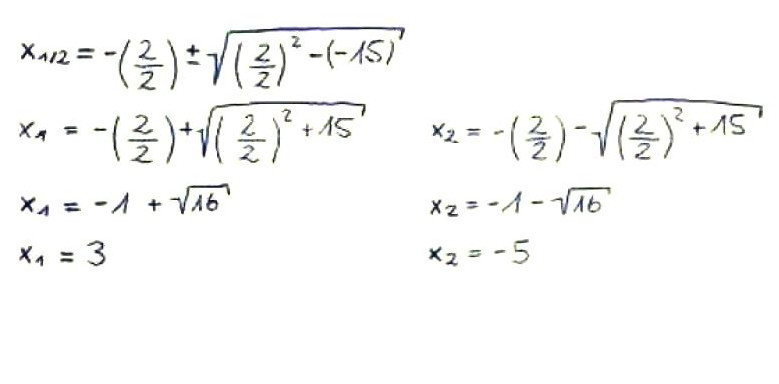3,74 von 5 Sterne
Loading...
Nullstellen berechnen kommt immer mal wieder im Matheunterricht vor. Deshalb ist es wichtig zu wissen, was Nullstellen sind und wie man sie ermittelt.
Im folgenden Artikel erklären wir dir Schritt für Schritt, wie du die Nullstellen einer Funktion findest.
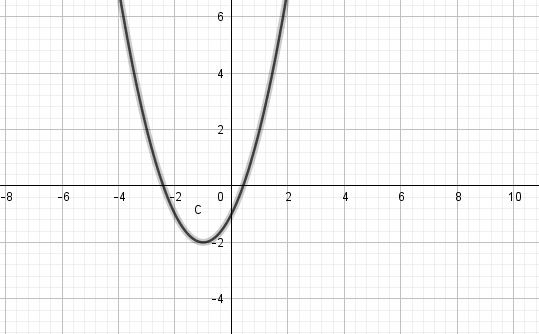
Wenn du den Graphen einer Funktion zeichnest, kann es sein, dass der Graph die x-Achse schneidet. An diesen Schnittpunkten mit der x-Achse, findest du dann die Nullstellen.
Deswegen beträgt y = 0.
Dabei kann es sein, dass ein Graph keine Nullstelle, genau eine Nullstelle oder mehrere Nullstellen hat.
Dieser Graph hat zum Beispiel zwei Nullstellen, weil zwei mal die x-Achse geschnitten wird.
Nullstellen einer Funktion berechnen – so geht’s
Nullstellen berechnen: Lineare Funktion
Im ersten Schritt setzen wir nun die Null für y bzw. f(x) ein.
Beispiel 1:f(x)=2x-6
Diese Funktion ist linear. Nachdem wir die Null eingesetzt haben erhalten wir:
0=2x-6
Im nächsten Schritt musst du die Gleichung dann nach x auflösen. Somit machst du also Äquivalenzumformungen:
⇔0=2x-6 |+6
⇔ 6=2x |:2
⇔ 3=x
Als Ergebnis erhältst du die Nullstelle. Der Punkt an dem du die Nullstelle im Koordinatensystem findest, ist dann (3/0).
Nullstellen berechnen: Quadratische Funktion
Beispiel 2: f(x)=x²+4x-5
Das zweite Beispiel ist eine quadratische Funktion. Im ersten Schritt setzt du für f(x) wieder die Null ein.
0=x²+4x-5
Im zweiten Schritt musst du die pq-Formel bei quadratischen Funktionen anwenden.
pq-Formel: \displaystyle x_{1,2}=-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}
Für p setzt du nun die Zahl ein, die vor dem x steht. Bei dieser Gleichung ist das also die 4. Für q setzt du die Zahl ein, die alleine ohne x steht. In diesem Beispiel ist das die (-5).
Damit ergeben sich die Nullstellen (1/0) und (-5/0).
Was muss ich bei der pq-Formel beachten?
Bei der pq-Formel muss man darauf achten, dass vor dem x² keine Zahl mehr steht.
Wenn die Funktion f(x)=2x²+6x-4 lautet, muss die Funktion erst durch 2 geteilt werden, bevor du in die Formel einsetzt. Danach steht keine Zahl mehr vor dem x²:
0=2x²+6x-4 |:2
⇔ 0=x²+3x-2
Beachte, dass du hier alle Teile durch 2 teilst, also auch die Zahl vor dem x und die Zahl, die alleine steht.
Merke: Um die pq-Formel anwenden zu können, muss die Funktion folgende Form haben:
f(x)=x²+ax+b (a und b stehen für beliebige Zahlen)
Nullstellen berechnen: e-Funktion
Viele e-Funktionen haben keine Nullstellen. Beispielsweise hat f(x)=\displaystyle e^{x} keine Nullstellen, weil die Funktion sich der x-Achse nur annähert. Aber sie schneidet sie nicht.
Das liegt daran, dass e hoch irgendeine Zahl nie gleich Null wird. Damit die e-Funktion Nullstellen hat, braucht sie beispielsweise den Zusatz -2.
Beispiel 3: f(x)=\displaystyle e^{x-3}-2
Nun kannst du die Funktion gleich Null setzen.
0=\displaystyle e^{x-3}-2
Im nächsten Schritt löst du die Funktion so auf, dass auf der linken Seite nur noch das e mit seinem Exponenten steht.
0=\displaystyle e^{x-3}-2 |+2
⇔ 2=\displaystyle e^{x-3}
Danach löst du die Funktion wie folgt mit dem natürlichen Logarithmus auf.
2=\displaystyle e^{x-3} |ln
⇔ ln2=x-3
⇔ 0,693=x-3 |+3
⇔ 3,693=x
Somit liegt die Nullstelle bei (3,693/0).
Nullstellen ablesen – wie geht das?
Manchmal sind Funktionen in folgender Form angegeben:
Beispiel 4: f(x)=(x-3)(x+4)
Diese Form nennt man die faktorisierte Form, da die Funktion in zwei Faktoren (Klammern) dargestellt wird. An dieser Stelle kannst du die Nullstellen ablesen, indem du die Klammern einzeln gleich der Null setzt.
x-3=0 |+3
⇔ \displaystyle x_1=3
x+4=0 |-4
⇔ \displaystyle x_2=(-4)
Dadurch wird eine Klammer zur Null und du würdest Null mal die andere Klammer rechnen. Dies muss also immer Null ergeben. Hier wurde beispielsweise die 3 eingesetzt:
(3-3)(3+4)=0
Somit ergeben sich bei der Funktion die Nullstellen (3/0) und (-4/0).
Nullstellen berechnen: Funktion 3. Grades – in 3 einfachen Schritten
Funktionen 3. Grades erkennt man daran, dass der höchste Exponent eine 3 ist.
Beispiel 5: f(x)=x³+x²-17x+15
Schritt 1: Errate eine Nullstelle
Dazu setzt du einfach Zahlen wie 0;1;2;-1;-2 für x ein. Dies machst du bis das Ergebnis Null ist.
f(0)=0³+0²-17×0+15
f(0)=15
Somit ist (0) keine Nullstelle.
f(1)=1³+1²-17×1+15
f(1)=0
Folglich hast du (1) als Nullstelle erraten.
Schritt 2: Polynomdivision anwenden
Bei der Polynomdivision teilst du die Funktion dann schriftlich durch (x minus die geratene Nullstelle).
Schritt 3: pq-Formel anwenden
Die pq-Formel kannst du einfach wieder wie im zweiten Beispiel verwenden. Dadurch ergeben sich neben der geratenen Nullstelle (1/0), noch die Nullstellen (3/0) und (-5/0).
Nullstellen bestimmen – Merke
Art der Funktion | Ermittlung der Nullstellen |
Lineare Funktionen | Funktion gleich Null setzen und nach x auflösen |
Quadratische Funktion | pq-Formel anwenden |
Faktorisierte Form | Nullstellen ablesen |
Ganzrationale Funktionen | Polynomdivision anwenden |
e-Funktionen | natürlichen Logarithmus verwenden |
Nullstellen berechnen: Aufgaben
Finde die Nullstellen. Danach runde, wenn nötig, auf bis zu zwei Nachkommastellen.
f(x)= 7x-14
g(x)= -6x-2
h(x)=x²+5x-1
i(x)= -2x²+1,8x+3,6
f(x)=7x-14
⇔0=7x-14 |+14
⇔14=7x |:7
⇔2=x
g(x)= -6x-2
⇔0=-6x-2 |+2
⇔2=-6x |:(-6)
⇔ -(1/3)=x
h(x)=x²+5x-1
\displaystyle x_{1,2}=-\dfrac{5}{2}\pm\sqrt{\left(\dfrac{5}{2}\right)^2-(-1)}\displaystyle x_1≈0,19
\displaystyle x_2≈ -5,19
i(x)= -2x²+1,8x+3,6
⇔0= -2x²+1,8x+3,6 |:(-2)
⇔0=x²-0,9x-1,8
\displaystyle x_{1,2}=-\dfrac{(-0,9)}{2}\pm\sqrt{\left(\dfrac{(-0,9)}{2}\right)^2-(-1,8)}\displaystyle x_1≈1,87
\displaystyle x_2≈ -0,97
Finde die Nullstellen. Danach runde, wenn nötig, auf bis zu zwei Nachkommastellen.
f(x)=x³+x²-10x+8
g(x)=\displaystyle e^{x+1}-9
f(x)=x³+x²-10x+8
f(1)=0
x³+x²-10x+8 : (x-1)=x²+2x-8
\displaystyle x_{2,3}=-\dfrac{2}{2}\pm\sqrt{\left(\dfrac{2}{2}\right)^2-(-8)}\displaystyle x_2=2
\displaystyle x_3=-4
g(x)=\displaystyle e^{x+1}-9
⇔0=\displaystyle e^{x+1}-9 |+9
⇔9=\displaystyle e^{x+1} |ln
⇔ln9=x+1 |-1
⇔x≈1,20
Lies die Nullstellen ab.
f(x)=(x-4)(x+3,76)
g(x)=(x+5)(x+3)
h(x)=(x-4,7)(x-5,8)
i(x)=(x+1)(x-2)
f(x)=(x-4)(x+3,76)
\displaystyle x_1=4 \displaystyle x_2= -3,76
g(x)=(x+5)(x+3)
\displaystyle x_1= -5 \displaystyle x_2 = -3
h(x)=(x-4,7)(x-5,8)
\displaystyle x_1=4,7 \displaystyle x_2=5,8
i(x)=(x+1)(x-2)
\displaystyle x_1= -1 \displaystyle x_2=2
Bist du schon optimal für deinen Mathekurs ausgestattet?
Nullstelle berechnen – FAQ
Was sind Nullstellen einer Funktion?
Schnittpunkte einer Funktion mit der x-Achse
Wann gibt es eine Nullstelle?
Immer wenn der Graph einen oder mehrere Schnittpunkte mit der x-Achse hat, gibt es Nullstellen.
Was ist die Nullstelle bei einer Parabel?
Bei der Normalparabel f(x) = x^2 liegt die Nullstelle bei (0/0). Wenn der Graph verschoben wird, verschieben sich auch die Nullstellen.
Wie kann man die Nullstelle genau ablesen?
Um die Nullstelle ablesen zu können, muss die Funktion in der faktorisierten Form angegeben sein.
Kann eine Parabel nur eine Nullstelle haben?
Ja, dann liegt der Scheitelpunkt des Graphen genau auf der x-Achse.
Konntest du die Rechenwege gut nachvollziehen?
Erzähle uns gerne in den Kommentaren, ob dir die Erklärungen geholfen haben!
Falls deine Schwierigkeiten in Mathe oder anderen Fächern mal über Nullstellen hinausgehen, lohnt es sich vielleicht einen Nachhilfelehrer um Unterstützung zu bitten.
Wenn du aber noch mehr über Mathe lernen willst, helfen dir vielleicht unsere Artikel zum Berechnen vom Schnittpunkt zweier Geraden, zum Arithmetischen Mittel und zu linearen Gleichungen.
Alles verständlich?
In jedem unserer Artikel steckt eine Menge Arbeit. Zeig uns doch durch eine Bewertung, ob du den Artikel gut fandst. Wir danken dir vielmals!
3,74 von 5 SterneLoading...