Du bist dir unsicher, wie man die Lösungen einer quadratischen Gleichung mithilfe der pq-Formel berechnet? Dann bist du bei uns genau richtig. Hier werden wir dir die pq- Formel veranschaulichen und mit Beispielen erklären, wie man sie anwendet.
pq-Formel – Erklärung
Die Pq-Formel kann verwendet werden, um quadratische Funktionen oder quadratische Gleichungen zu lösen. Quadratische Gleichungen besitzen immer mindestens ein x², aber keine höheren Potenzen wie x³ oder x4.
Damit du eine Aufgabe mit der pq-Formel lösen kannst, brauchen wir noch die entsprechende Formel.
Wie lautet die pq-Formel?
Wie der Name schon sagt, benötigt man für die pq-Formel p und q. P ist immer die Zahl, die vor x steht, und q ist die Zahl ohne x. p und q sind reelle Zahlen und x eine reelle Variable.
x² – 7 x + 2 = 0 ⇛ p = – 7
x² – 7 x + 2 = 0 ⇛ q = 2
x¹ und x² stehen dafür, dass du zwei Lösungen berechnen kannst.
pq-Formel anwenden
Um die pq-Formel anwenden zu können, muss die quadratische Gleichung vor dem Lösen in die Normalform umgewandelt werden.
Quadratische Gleichungen haben die Form:
Beispiel für eine quadratische Gleichung:
2 x² + 6 x + 2 = 0 → a = 2 b = 6 c = 2
Die Normalform von quadratischen Gleichungen sieht folgendermaßen aus:
Beispiel einer quadratischen Gleichung in Normalform:
2 x² + 6 x + 2 = 0 | : 2
x² + 3 x + 1 = 0
Die 2 vor dem x² muss weg, da die Normalform kein Vorfaktor hat. Deshalb wird die quadratische Gleichung durch 2 dividiert. Zahlen aus deiner Gleichung kannst du nun in die pq-Formel einsetzen. Wie das geht, erklären wir dir im nächsten Kapitel.
Es werden vier Typen von quadratischen Gleichungen in Normalform unterschieden. In der Tabelle siehst du für jeden Gleichungstyp ein Beispiel.

Die pq-Formel können wir bei allen vier Typen anwenden. Allerdings empfiehlt sich eine Anwendung nur für gemischtquadratische Gleichungen mit absolutem Glied, da für die anderen Typen einfachere Lösungsverfahren herrschen.
Quadratische Gleichungen lösen mithilfe der pq-Formel
Wenn die quadratische Gleichung in Normalform vorliegt, kannst Du die pq-Formel verwenden. Dies schauen wir uns an einem Beispiel an.
Beispiel: Löse die Gleichung – 4 x² – 24 x – 32 = 0
1. Wie du siehst, ist unsere Gleichung nicht in der Normalform. Du musst die Gleichung durch – 4 dividieren, um das negative Vorzeichen und die 4 wegzukriegen.
– 4 x² – 24 x – 32 = 0 | : (-4)
x² + 6 x + 8 = 0
2. Aus der Normalform kannst du dann p und q herauslesen. Unser p ist die 6, da sie vor dem x steht. Die 8 ist unser q, da sie ohne die Variable x steht.
x² + 6 x + 8 = 0
p = 6 q = 8
3. Nun kannst du p und q in die Lösungsformel einsetzen. Du setzt für p die 6 und für q die 8 ein.
4. Wenn es möglich ist, vereinfachst du .
Du bekommst als Ergebnis -3, da = – 3 sind. Als nächstes berechnest du das Quadrat in der Wurzel.
Du rechnest = 3 und quadrierst die 3. Als Ergebnis erhältst du die Zahl 9.
x₁,₂ = – 3 ± √9 – 8
5. Anschließend rechnest du den Wert in der Wurzel aus und bekommst als Ergebnis eine 1. Anschließend ziehst du die Wurzel aus 1.
x₁,₂ = – 3 ± √1
6. Jetzt kannst du die Lösungen berechnen. Du rechnest einmal -3 + 1 = -2 und einmal -3 – 1 = -4 . Als Ergebnis erhältst du -2 und -4.
x₁,₂ = – 3 ± 1
x₁ = – 3 + 1 = -2 x₂ = – 3 – 1 = -4
7. Zum Schluss schreibst du die Lösungsmenge auf.
L = { -4 ; -2 }
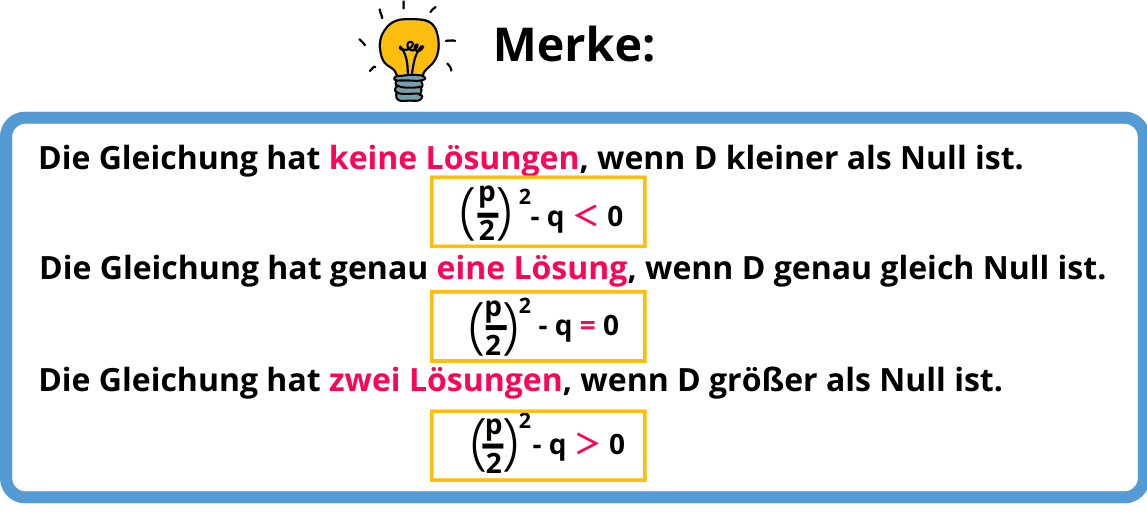
Die Diskriminante bei der pq-Formel
Die Diskriminante ist der Term , der unter der Wurzel steht. Sie wird oft mit D abgekürzt. Anhand der Diskriminante D der pq-Formel lässt sich die Anzahl der Lösungen einer quadratischen Gleichung angeben.
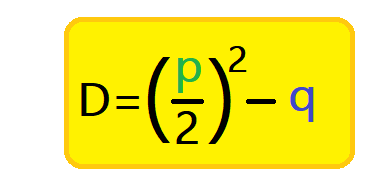
pq-Formel Beispiele
Die pq-Formel kann eine verschiedene Anzahl von Lösungen liefern. Damit du die diese kennenlernst, zeigen wir dir drei Beispiele.
pq-Formel Beispiel mit zwei Lösungen
Gegeben ist die quadratische Gleichung: 3 x² + 3 x = 18
1. Zuerst bringst du die Gleichung in die Normalform. Alle Werte auf der rechten Seite bringst du auf die linke Seite, sodass nach dem Gleichheitszeichen eine 0 steht.
3 x² + 3 x = 18 | -18
3 x² + 3 x – 18 = 0
2. Da die Gleichung noch immer nicht in der Normalform ist, muss es durch die 3 dividiert werden.
3 x² + 3 x – 18 = 0 | : 3
x² + x – 6 = 0
3. Du setzt für p die Zahl 1 in die Formel ein. Für q setzt du die -6 ein. Hierbei musst du beachten das Vorzeichen mitzunehmen.
p = 1 q = – 6
4. Du rechnest nun das Quadrat in der Wurzel aus. Anschließend rechnest du den Wert in der Wurzel aus.
x₁,₂ =
5. Die Wurzel aus kannst du ziehen und bekommst als Ergebnis 2,5. Nachdem du das gemacht hast kannst du die Lösungen für x₁ und x₂ berechnen.
x₁,₂ = – 0,5 ± 2,5
x₁ = – 0,5 + 2,5 = 2 x₂ = – 0,5 – 2,5 = -3
6. Zu guter Letzt schreibst du noch die Lösungsmenge auf.
L = { -3 ; 2 }
pq-Formel Beispiel mit einer Lösung
Gegeben ist die quadratische Gleichung: x² – 8 x + 16 = 0
1. Da die Gleichung schon in der Normalform vorliegt, kannst du p und q herauslesen und diese in die Lösungsformel direkt einsetzen. Für p setzt du – 8 ein und für q die 16 ein.
p = – 8 q = 16
2. Als Nächstes vereinfachst du und berechnest das Quadrat in der Wurzel. Danach rechnest du den Wert in der Wurzel aus. Die Gleichung hat genau eine Lösung, da D genau gleich Null ist.
x₁,₂ = 4 ± √16 – 16
x₁,₂ = 4 ± √0
3. Die Wurzel von 0 ist 0 und du erhältst genau eine Lösung.
x₁,₂ = 4 ± 0
x₁,₂ = 4
4. Die Lösungsmenge der quadratischen Gleichung schreibst du zum Schluss auf.
L = { 4 }
pq-Formel Beispiel mit keiner Lösung
Gegeben ist die quadratische Gleichung: x ² – 5 x + 8 = 0
1. An dieser Stelle brauchst du die Gleichung nicht in die Normalform zu bringen, da diese bereits schon vorliegt. p und q kannst du aus der Gleichung herauslesen und diese in der Formel einsetzen.
p = – 5 q = 8
2. Das Quadrat in der Wurzel kannst du dann ausrechnen. Anschließend berechnest du den Wert in der Wurzel.
3. Da du aus einer negativen Zahl die Wurzel nicht ziehen darfst, hat die Gleichung keine Lösung.
⚡Abbruch
4. Die Lösungsmenge für keine Lösung sieht folgendermaßen aus.
L= { }
pq-Formel Aufgaben
Rechne die folgenden 3 Aufgaben und schaue, ob die pq-Formel richtig anwendest. Anschließend kannst du durch einen Klick deine Lösung überprüfen.
1. Löse die quadratische Gleichung mit Hilfe der pq-Formel:
– 4 x² + 8 x + 12 = 0
– 4 x² + 8 x + 12 = 0 | : (-4)
x² – 2 x – 3 = 0
p = – 2 q = – 3
x₁,₂ = 1 ± √1 +3
x₁,₂ = 1 ± √4
x₁,₂ = 1 ± 2
x₁= 1 + 2 = 3 x₂= 1 – 2 = -1
L = { -1 ; 3 } ⇒ Zwei Lösungen
2. Löse die quadratische Gleichung mit Hilfe der pq-Formel:
x² – 6 x + 20 = – 4
x² – 6 x + 20 = – 4 |+ 4
x² – 6 x + 24 = 0
p = – 6 q = 24
x₁,₂ = 3 ± √9 – 24
x₁,₂ = 3 ± √-15 ⚡Abbruch
L= { } ⇒ Keine Lösung
3. Löse die quadratische Gleichung mit Hilfe der pq-Formel:
8 x² + 16 x = – 8
8 x² + 16 x = – 8 | + 8
8 x² + 16 x + 8 = 0 | : 8
x² + 2 x + 1 = 0
p = 2 q = 1
x₁,₂ = – 1 ± √1 -1
x₁,₂ = – 1 ± √0
x₁,₂ = -1 ± 0
x₁,₂ = -1
L= { -1 } ⇒ Eine Lösung
FAQ
Wie lautet die pq - Formel?
Die pq-Formel lautet:
Was ist das P in der pq - Formel?
p ist die Zahl bei einer quadratischen Gleichung, die vor dem einzelnen x steht.
Beispiel: x² + 5 x + 2 = 0 ⇛ p = 5

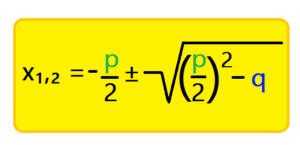
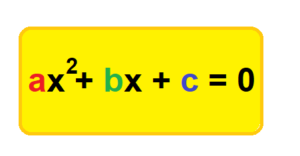
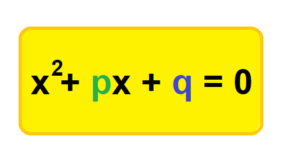

Ich verstehe die Lösungen der Beispiele 2 und 3 nicht
Zum Beispiel mit einer Lösung
p = – 8 q = 16
x₁,₂ = − −8/2 ± √(8/2)² −16
x₁,₂ = 4 ± √16 – 16
Warum nicht :
x₁,₂ = − −8/2 ± √( – 8/2)² −16
x₁,₂ = 4 ± √ –16 – 16
x₁,₂ = 4 ± √ –32
Entsprechend im Beispiel mit keiner Lösung
x₁,₂ = − -5/2 ± √(-5/2)² −8
x₁,₂ = 2,5 ± √25/4 – 8
Warum nicht :
x₁,₂ = 2,5 ± √ –25/4 – 8
x₁,₂ = 2,5 ± √ –6,25 – 8
x₁,₂ = 2,5 ± √ –14,25
Hallo, deine Frage lässt sich ganz einfach erklären. Wenn du eine negative Zahl hoch 2 rechnest, kommt immer eine positive Zahl dabei heraus. Beispielsweise für das erste: (-8/2) ist gleich -4. -4 hoch 2 ist das gleiche wie (-4) * (-4). Und minus mal minus ergibt plus. Deswegen kommt 16 und nicht -16 als Ergebnis heraus. Ich hoffe wir konnten dir deine Frage beantworten 🙂
Ich verstehe nicht woher ihr die zahlen für p&q nehmt. Kann ich da beliebige zahlen nehmen?
Du musst die Formel in die Normalform bringen, dann kannst du die Zahl, welche vor dem einzelnen X steht als p verwenden und die Zahl, die am Ende alleine steht, als q. Im Artikel findest du auch eine Beispielaufgabe die es verdeutlicht. Liebe Grüße