4,00 von 5 Sterne
Loading...
In diesem Artikel wird dir erklärt, wie man von einer Normalparabel zur allgemeinen Parabel 2. Ordnung gelangt. Hier wirst du außerdem alle Eigenschaften einer Parabel 2. Ordnung kennenlernen. Bereit, ein Profi zu werden?
Legen wir direkt los.
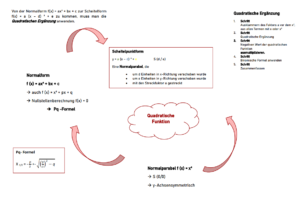
Eine quadratische Funktion ist eine Funktion, bei der das größte Polynom x² in der Gleichung ist. Der Graph der quadratischen Funktion ist eine Parabel. Deshalb spricht man ebenfalls über eine Parabelgleichung. Die Formel der quadratischen Funktion lautet:
Synonyme für quadratische Funktionen
- ganzrationale Funktion zweiten Grades
- Parabelgleichung
- allgemeine Normalform
f(x) = ax² + bx + c
Normalparabel – Was ist das?
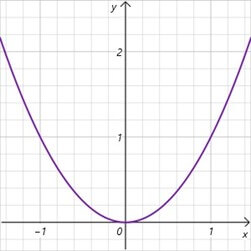
Die Normalparabel ist die einfachste und speziellste Parabel mit der Gleichung f(x) = x². Speziell, weil sie ihren Scheitelpunkt im Koordinatenursprung 0 (0/0) hat. Sie ist nach oben geöffnet und symmetrisch zur y-Achse.
Kommen wir zu den Eigenschaften. Durch diese können wir verstehen, wie sich eine quadratische Funktion – sprich eine Parabel – verändern kann.
Alle Eigenschaften auf einen Blick
Wie du oben sehen kannst, lautet die quadratische Funktionsformel f(x) = ax² + bx + c.
Um die Veränderung zu sehen, müssen wir diese Formel jedoch in die Scheitelform f(x) = a (x – d) ² + e umwandeln. Dies geht durch Anwendung der Quadratischen Ergänzung.
Nehmen wir dazu ein Beispiel: Für die quadratischen Funktion f(x) = 2x² – 4x – 2 lautet die Scheitelpunktform durch Anwendung der quadratischen Ergänzung f(x) = 2 (x – 1) ² – 4.
Dazu befolgst du am besten diese 5 Schritte:
Quadratische Ergänzung
f(x) = 2x² – 4x – 2
f(x) = 2 (x² – 2x) – 2
f(x) = 2 (x² – 2x + 1 – 1) – 2
f(x) = 2 (x – 1) ² – 2 – 2
f(x) = 2 (x – 1) ² – 4
Wichtig für dich zu verstehen ist, dass diese zwei Gleichungen in der Form vielleicht verschieden sind, aber es genau die gleiche Gleichung ist und dass die nur einen Graphen hat.
Machen wir weiter und nutzen dieses Beispiel, um die Eigenschaften besser zu verstehen.
Verschiebung in y – Richtung
Verschiebung in y – Richtung heißt, dass die Parabel nach oben und nach unten geöffnet werden kann.
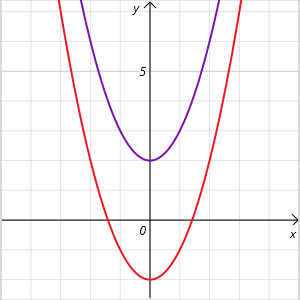
Bei einer Verschiebung nach oben addiert man ein e zu x²: f(x) = x² + e.
Bei einer Verschiebung nach unten subtrahiert man ein e zu x²: f(x) = x² – e.
Im obigen Schaubild siehst du zwei Parabeln: die erste wurde um 2 Einheiten nach oben verschoben, also heißt ihre Gleichung f(x) = x² + 2. Die zweite wurde um 2 Einheiten nach unten verschoben, somit heißt die Gleichung f(x) = x² – 2.
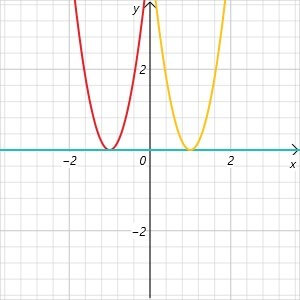
Verschiebung in x – Richtung
Bei der Verschiebung in x Richtung wird die Funktionsgleichung nach links oder nach rechts verschoben.
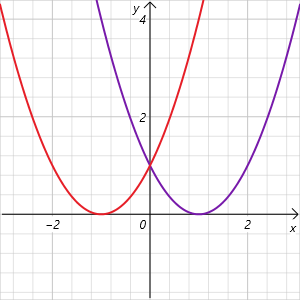
Bei einer Verschiebung nach rechts wird zur Normalparabel ein positives d hinzugefügt:
f(x) = (x – d) ².
Bei einer Verschiebung nach links wird zur Normalparabel ein negatives d hinzugefügt:
f(x) = (x + d) ².
Im obigen Schaubild siehst du zwei Parabeln: die erste wurde um eine Einheit nach links verschoben, also heißt ihre Gleichung f(x) = (x + 1) ². Die zweite wurde um eine Einheit nach rechts verschoben, somit heißt diese Gleichung f(x) = (x – 1) ².
Streckung und Stauchung
Du kannst auch eine Parabel strecken und stauchen.
Streckung und Stauchung in y-Richtung
Wenn in y-Richtung gestreckt bzw. gestaucht werden soll, wird der ganze Funktionsterm mit dem Faktor a multipliziert.
g(x) = a * f(x)
a* f(x), a > 1 – Streckung in y-Richtung
a* f(x), a < 1 – Stauchung in y-Richtung
Streckung und Stauchung in x-Richtung
Wenn in x-Richtung gestreckt bzw. gestaucht werden soll, wird der x-Wert mit dem Faktor a multipliziert.
g(x) = f(a*x)
f(a*x), a > 1 – Stauchung in x-Richtung
f(a*x), a < 1 – Streckung in x-Richtung
Ist das a negativ, dann wird der Graph an der x-Achse gespiegelt.
Soweit alles verstanden? Nein? Keine Sorge, ich habe dir eine Zusammenfassung als PDF-Datei hier unten zum Download erstellt, die du dir zu Hilfe nehmen kannst. Bei der zweiten Datei findest du Aufgaben mit Lösungen, die du zum üben benutzen kannst.
Quadratische Funktion – Zusammenfassung
Hier zur Zusammenfassung: PDF Zusammenfassung Quadratische Funktion
Quadratische Funktion – Aufgaben
Der Graph der Funktion h mit h(x) = ½ x² – x soll mit dem Faktor 3 in y-Richtung gestreckt werden. Gib die Funktionsgleichung des durch die Streckung entstandenen Funktionsgraphen an. Vereinfache die Gleichung so weit wie möglich.
h(x) = ½ x² – x
h(x) = 3 * (½ x² – x)
h(x) = 3/2x² – 3x
Quadratische Funktion – FAQ
Was ist eine Quadratische Funktion?
Eine quadratische Funktion ist eine Funktion, bei der das größte Polynom die x² in der Gleichung ist. Mann nennt sie auch Parabelfunktion, da ihr Graph eine Parabel ist.
Was ist der Unterschied zwischen einer quadratischen Funktion und der Scheitelform?
Der Unterschied liegt an die Darstellungsform der Gleichungen. Quadratische Funktion: f(x) = ax² +bx +c
Scheitelform: f(x) = a (x – d) ² +e
Der Graph ist identisch.
Was ist die Normalparabel?
Die Normalparabel ist die einfachste quadratische Funktion, bei der der Scheitelpunkt im Ursprung ist S (0/0). Ihre Gleichung lautet: f(x) = x².
Wie findest du diesen Artikel? Wir würden uns über eine Sternenbewertung freuen. Hast du Anmerkungen oder ein positives Feedback? Bitte lass uns in deinem Kommentar, wissen was du über unseren Artikel denkst. Wir danke dir sehr. 🙂 4,00 von 5 SterneLoading...
Dies könnte ebenfalls interessant für dich sein:
