3,57 von 5 Sterne
Loading...
Du willst bei einer Funktion die Monotonie bestimmen und weißt nicht weiter? Dann bist du hier richtig! Wir erklären dir alles zu dem Thema und beantworten deine Fragen. Am Ende des Artikels warten auch noch Übungsaufgaben auf dich, um dein Wissen sofort zu testen.
Monotonie Definition
Monotonie in der Mathematik gehört zum Thema Kurvendiskussion und wird im Matheunterricht häufig verwendet. Die Monotonie einer Funktion f(x) sagt aus, wie eine Funktion verläuft d.h. wie sie im Koordinatensystem aussieht.
Die Funktion wird immer von links nach rechts angeschaut und so bestimmt, ob sie steigt, oder fällt.
Da es hier darum geht, wie sich eine Funktion verhält, sprechen wir auch vom Monotonieverhalten. Man kann die Funktion auch in verschiedene Abschnitte einteilen und für jeden Abschnitte die Monotonie bestimmen.
Monotonie bestimmen – was sind die unterschiedlichen Monotonien?
- monoton steigend
–> Funktion steigt insgesamt, hat aber ebene oder fallende Bereiche
- streng monoton steigend
–> die Funktion steigt stetig
- monoton fallend
–> Funktion fällt insgesamt, hat aber ebene oder steigende Bereiche
- streng monoton fallend
–> die Funktion fällt stetig
In der folgenden Grafik sind die Monotonien der einzelnen Abschnitte der Funktion benannt. Insgesamt ist die Funktion monoton fallend.
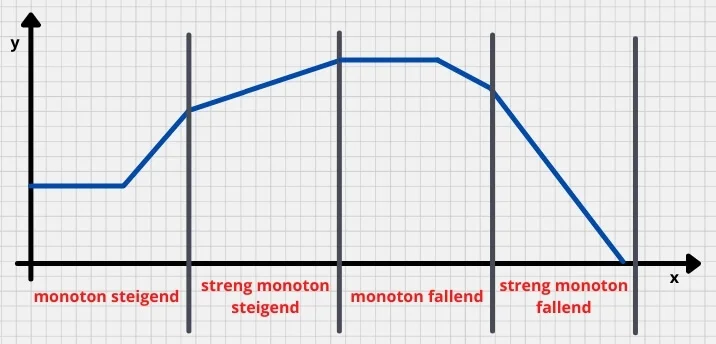
Welche Funktion ist monoton fallend und steigend?
Hier sind Beispiele für Funktionen mit verschiedenen Monotonie-Arten:
monoton steigend: f(x) = x⁵-6x
streng monoton steigend: f(x) = x+15
monoton fallend: f(x) = -x³
streng monoton fallend: f(x) = -9x
Wann liegt keine Monotonie vor?
Ist der komplette Graph einer Funktion perfekt senkrecht oder waagerecht, bezeichnet man ihn als konstant. Hier trifft keine der vier Arten von Monotonie zu, da sich der Graph nicht verändert. Die Funktion sieht zum Beispiel so aus:
f(x) = 2
Der Wert der Funktion ist immer 2, egal wie x lautet.
Steigung bestimmen inklusive Beispiele
Willst du die Monotonie einer Funktion ermitteln, musst du zuerst die Extrempunkte berechnen. Die Monotonie kann rechts und links dieser Stellen unterschiedlich sein. Deshalb ist es wichtig, die Funktion in Intervalle um und neben diesen Extrempunkten einzuteilen.
Was sind Monotonieintervalle?
Monotonieintervalle sind einzelne Abschnitte einer Funktion z.B. vom Punkt x=-4 bis x=0: Intervall [-4;0]. Für jedes Intervall kann die Monotonie einzeln angegeben werden.
Wie berechne ich die Monotonie?
Willst du die Monotonie bestimmen, gibt es zwei Alternativen für dich. Für beide benötigst du die erste Ableitung der Funktion. Die erste Ableitung einer Funktion ist nämlich ihre Steigung und genau die wollen wir ja bei der Monotonieberechnung herausfinden.
Die ersten beiden Schritte sind also bei beiden Alternativen die gleichen.
Wir berechnen die Nullstellen der ersten Ableitung, da dort die Steigung der Ursprungsfunktion 0 ist und es sich deshalb um eine Extremstelle handelt.
Brauchst du noch ein bisschen Hilfe beim Berechnen der Nullstelle(n)? Dann haben wir den perfekten Artikel für dich!
Alternative A
(mit zweiter Ableitung):
- Erste Ableitung der Funktion berechnen
- Erste Ableitung = 0 setzen, um die Nullstelle(n) der Ableitung zu ermitteln
- Zweite Ableitung berechnen
- Nullstelle(n) der ersten Ableitung in die zweite Ableitung einsetzen und Funktionswert der zweiten Ableitung ausrechnen
- Extremstelle(n) ermitteln: Ist der Wert von 5. < 0, handelt es sich um einen Hochpunkt, bei f’’(x) > 0 ist es ein Tiefpunkt und bei f’’(x) = 0 ein Wendepunkt.
- Die Monotonie des Graphen um die Extremstellen bestimmen.
Alternative B
(ohne zweite Ableitung):
- Erste Ableitung der Funktion berechnen
- Erste Ableitung = 0 setzen, um die Nullstelle(n) der Ableitung zu ermitteln
- Intervalle um die Nullstelle(n) der ersten Ableitung aufstellen
- Steigung/erste Ableitung von beliebigen Zahlen in den Intervallen berechnen
- Vorzeichen der Intervalle bestimmen
- Mit den Vorzeichen der Intervalle die Steigung um die Extrempunkte der Funktion ermitteln
f’’(x) < 0 → Hochpunkt
f’’(x) > 0 → Tiefpunkt
Bei einem Hochpunkt fällt die Funktion links und rechts davon streng monoton.
Bei einem Tiefpunkt steigt die Funktion links und rechts davon streng monoton.
Beispiel 1: f(x) = 3x²-12x+2
Alternative A
(mit zweiter Ableitung):
- Erste Ableitung
f’(x) = 6x-12 - Nullstelle(n) der ersten Ableitung bestimmen
6x-12 = 0
6x = 12
x = 2
Bei x = 2 hat die Ableitung eine Nullstelle f(2) = -10 → bei (2/-10) hat die Funktion eine Extremstelle. - Zweite Ableitung berechnen
f’’(x) = 6 - Nullstelle(n) der ersten Ableitung in die zweite einsetzen
f’’(2) = 6 - Extremstelle(n) bestimmen
f’’(2) = 6 > 0 → (2/-10) ist ein Tiefpunkt. - Die Monotonie des Graphen um die Extremstelle(n) bestimmen
]-∞; 2] streng monoton fallend
[2; ∞[ streng monoton steigend
Alternative B
(ohne zweite Ableitung):
- Erste Ableitung
f’(x) = 6x-12 - Nullstelle(n) der ersten Ableitung bestimmen
6x-12 = 0
6x = 12
x = 2
Bei x = 2 hat die Ableitung eine Nullstelle f(2) = -10 → bei (2/-10) hat die Funktion eine Extremstelle. - Intervalle um die Nullstelle(n) der ersten Ableitung aufstellen
Nullstelle der Ableitung bzw. Extrempunkt der Funktion: x = 2
Intervalle: ]-∞;2] und [2;∞[ - Erste Ableitung von beliebigen Zahlen in den Intervallen um die Extremstelle(n) herum berechnen
f’(x) = 6x-12
f’(1) = -6
f’(3) = +6 - Vorzeichen der Intervalle bestimmen
]-∞;2] → negatives Vorzeichen
[2;∞[ → positives Vorzeichen - Mit den Vorzeichen der Intervalle die Steigung um die Extrempunkte ermitteln
Im Intervall ]-∞;2] also links vom Extrempunkt fällt die Funktion streng monoton.
Im Intervall [2;∞[ also rechts vom Extrempunkt steigt die Funktion streng monoton.
Wie du siehst, ist es egal, mit welchem Weg wir die Monotonie bestimmen. Wir kommen mit beiden Wegen auf das gleiche Ergebnis.
f’(x) = Ableitung an einer bestimmten Stelle x
f’(x) > 0 → streng monoton steigend
f’(x) ≥ 0 → monoton steigend
f’(x) < 0 → streng monoton fallend
f’(x) ≤ 0 → monoton fallend
Beispiel 2: f(x) = 5x+20
Alternative A
(mit zweiter Ableitung):
- Erste Ableitung
f’(x) = 5 - Nullstelle(n) der ersten Ableitung bestimmen
Die Ableitung ist überall 5. Das heißt, die Ableitung hat keine Nullstelle(n) und die Funktion keine Extremstelle(n). - Zweite Ableitung berechnen
f’’(x) = 0 - Nullstelle(n) der ersten Ableitung in die zweite einsetzen
Ist hier nicht möglich, da die erste Ableitung keine Nullstelle hat. - Extremstelle(n) bestimmen
Es gibt hier bei dieser Funktion keine Extremstellen. - Die Monotonie des Graphen um die Extremstelle(n) bestimmen
Die erste Ableitung und damit die Steigung der Funktion ist überall 5. Die Funktion ist also streng monoton steigend.
Auch hier ist das Ergebnis bei beiden Wegen gleich.
Alternative B
(ohne zweite Ableitung):
- Erste Ableitung
f’(x) = 5 - Nullstellen der ersten Ableitung bestimmen
Die Ableitung ist überall 5. Das hießt, die Ableitung hat keine Nullstelle(n) und die Funktion keine Extremstelle(n). - Intervalle um die Nullstellen der ersten Ableitung aufstellen
Da die Funktion keine Extremstellen hat, gibt es auch keine Intervalle darum. Das einzige Intervall ist ]-∞;∞[. - Erste Ableitung von beliebigen Zahlen in den Intervallen um die Extrempunkte herum berechnen
Bei jedem beliebigen x ist die erste Ableitung +5. - Vorzeichen der Intervalle bestimmen
Das Vorzeichen ist überall +. - Mit den Vorzeichen der Intervalle die Steigung um die Extrempunkte ermitteln
Die Steigung ist überall 5. Die Funktion ist also streng monoton steigend.
Monotonie bestimmen als streng monoton steigend
Wenn eine Funktion überall streng monoton steigend ist, hat sie keine Extrempunkte sondern verläuft stetig steigend.
Damit dies der Fall ist, muss die Ableitung bzw. die Steigung der Funktion immer den gleichen Wert (>0) haben. Hat die Ableitung mindestens eine Nullstelle, beträgt die Steigung dort 0. Deshalb ist die Funktion dann nicht mehr streng monoton steigend, sondern nur noch monoton steigend.
Beispiel:
f(x) = x+6
f’(x) = 1
Die Steigung beträgt überall 1.
Das Gleiche gilt für streng monoton fallende Funktionen.
Monotoniebestimmung ohne Ableitung – so geht’s
Wie du oben gesehen hast, brauchst du für beide Wege der Monotoniebestimmung, die wir hier gezeigt haben, die erste Ableitung der Funktion.
Es gibt aber eine Möglichkeit, wie du die Monotonie bestimmen kannst, ohne die Funktion abzuleiten.
Du kannst den Graphen der Funktion einfach aufzeichnen und grafisch analysieren. Jedoch gibt es hier den Nachteil, dass du den Graphen vermutlich nicht 100% exakt zeichnen und so die Monotonie und die Intervalle nur grob bestimmen kannst.
Fazit: Jetzt kennst du alle Wege, wie du bei einer Funktion die Monotonie bestimmen kannst. Mit den Aufgaben weiter unten kannst du direkt üben.
Hast du Fragen oder Anregungen? Schreib sie uns gerne in die Kommentare.
Steigung feststellen – Aufgaben mit Lösungen
Bei diesen Aufgaben sind immer die Ausgangsfunktionen gegeben und du sollst ausrechnen, in welchen Intervallen die Funktion welche Monotonie hat.
Klicke einfach auf die Aufgaben, um die Lösung anzuzeigen.
f'(x) = 8x-40
8x-40=0 –> x=5
f'(4) = -16; f'(6) = 8 –> Tiefpunkt bei x=5
]-∞;5] s.m.f.
[5;∞[ s.m.s.
f'(x) = 3x²-147
3x²-147=0 –> x=7; x=-7
f'(-8) = 45; f'(-6) = -39; f'(6) = -39; f'(8) = 45 –> HP bei x = -7; TP bei x = 7
]-∞;-7] s.m.s.
[-7;7[ s.m.f
[7;∞[ s.m.s.
f'(x) = 10
f'(x) hat keine Nullstelle -> f(x) hat keine Extrema
]-∞;∞[ s.m.s.
Streng monoton steigend sind nicht nur einige Kurven, sondern auch deine Noten, wenn du beim Nachhilfe-Team bist!
In zahlreichen Städten Deutschlands, von Berlin, über Köln bis nach München, sind wir tätig und geben fleißig Nachhilfe. Gerne auch bei dir Zuhause oder direkt Online durch unser beliebtes Mathematik Online Lernprogramm!
Schau unter den Links gerne mal vorbei! Wir freuen uns auf dich.