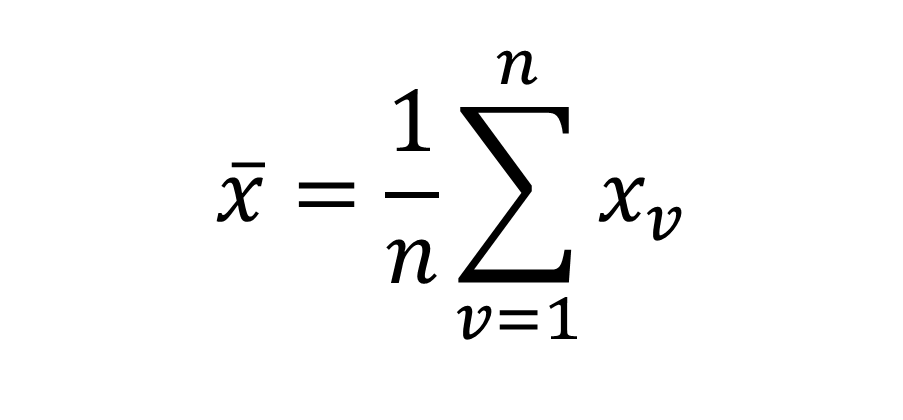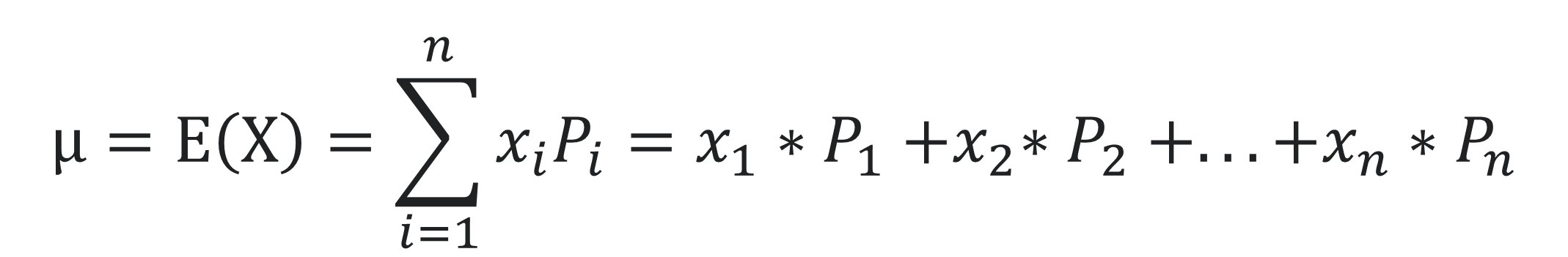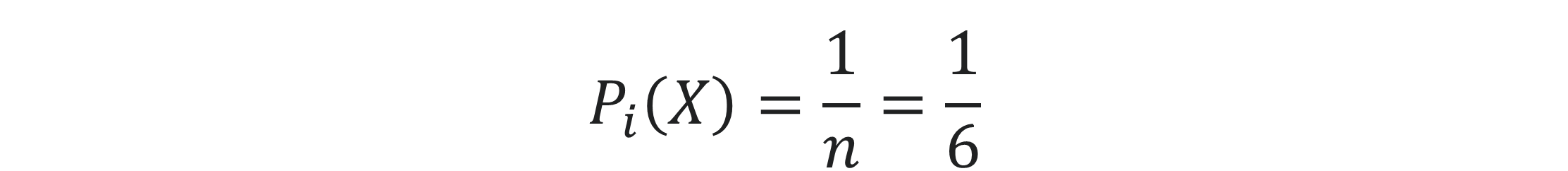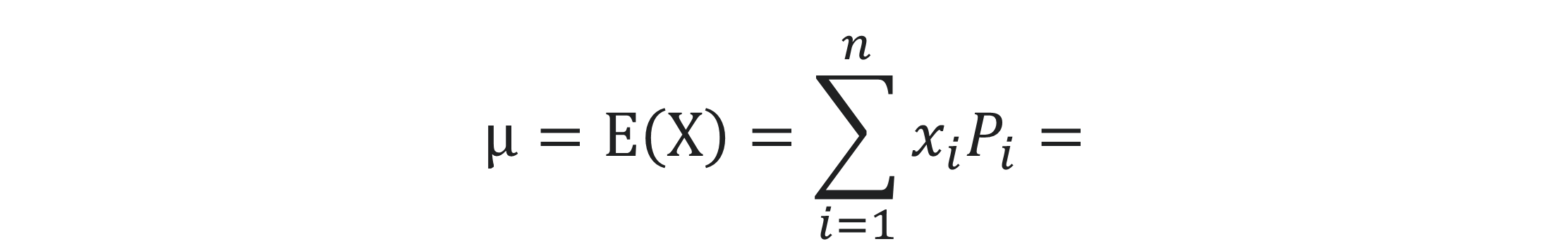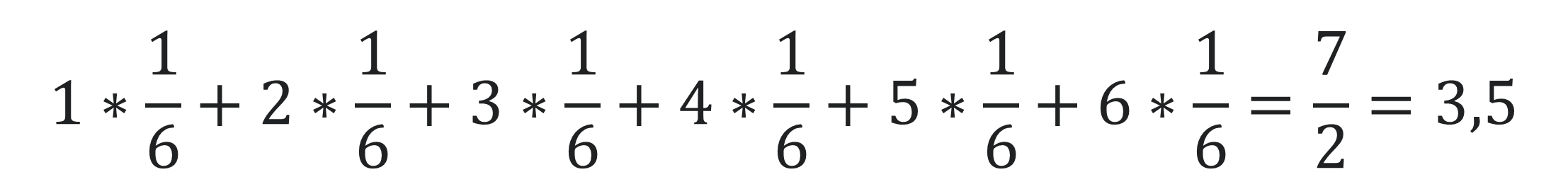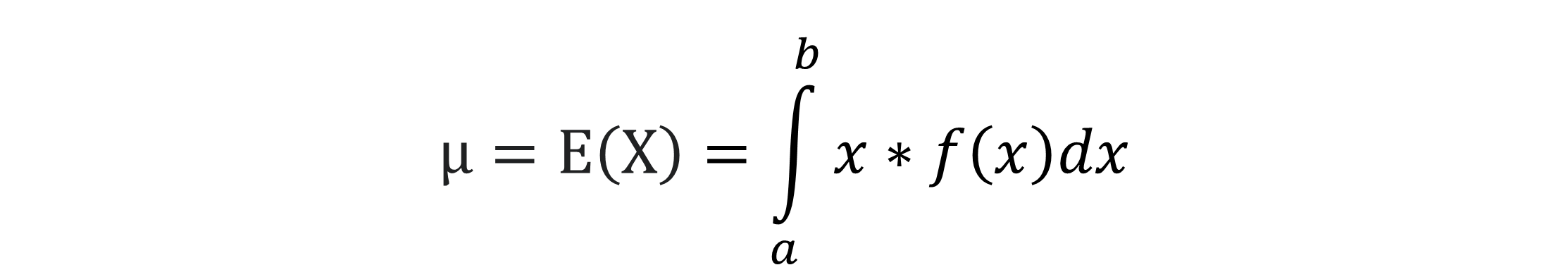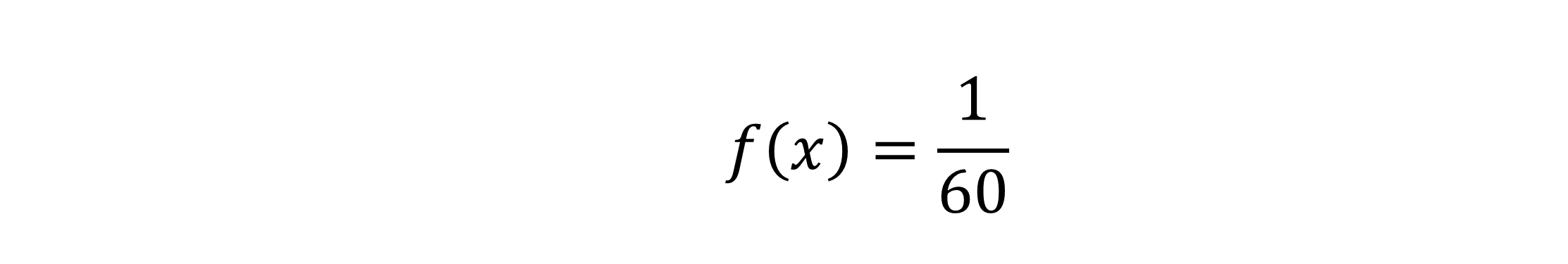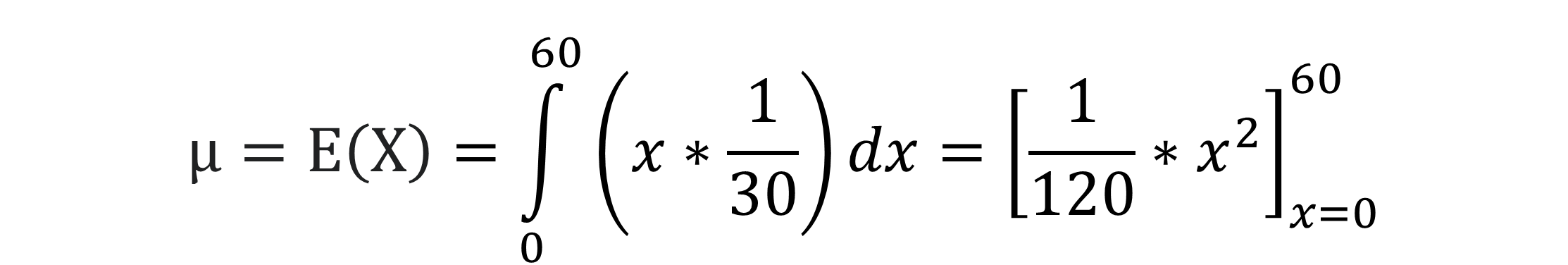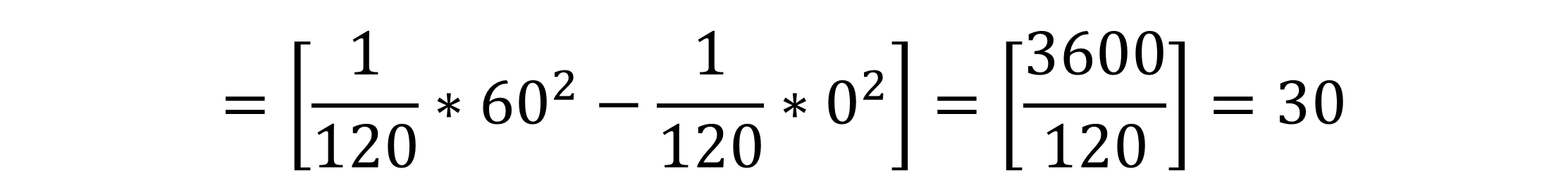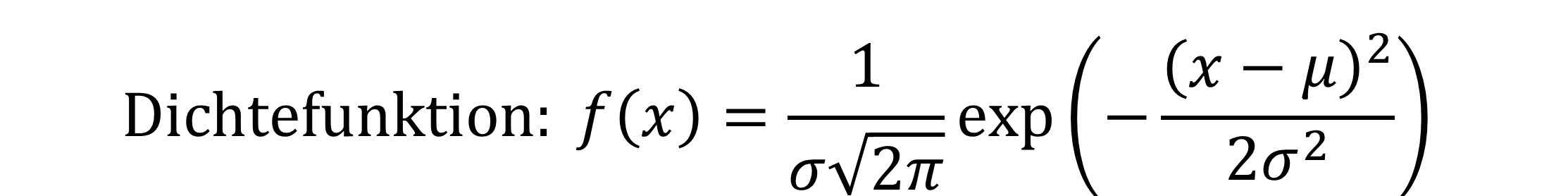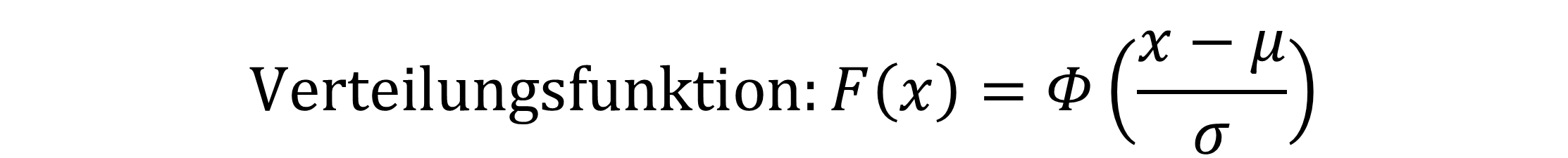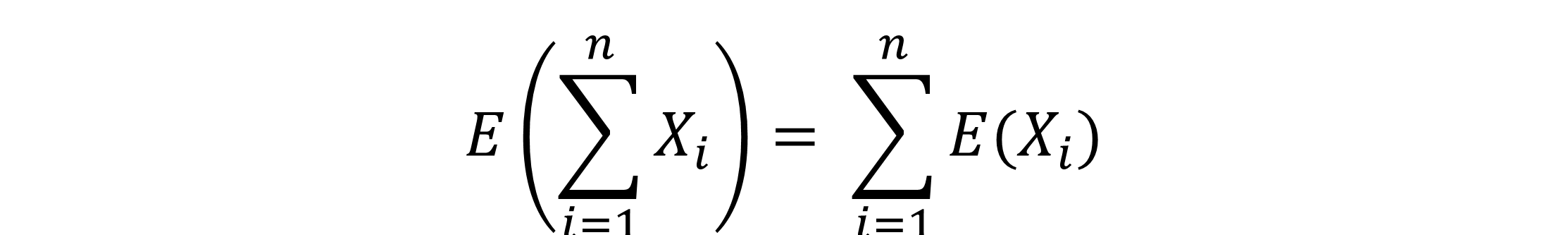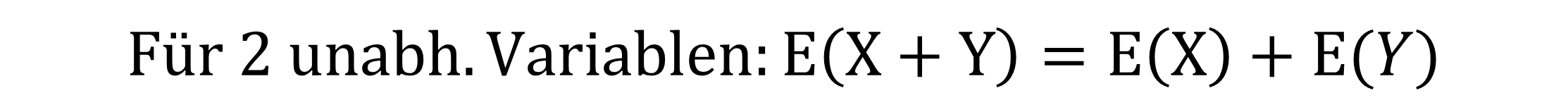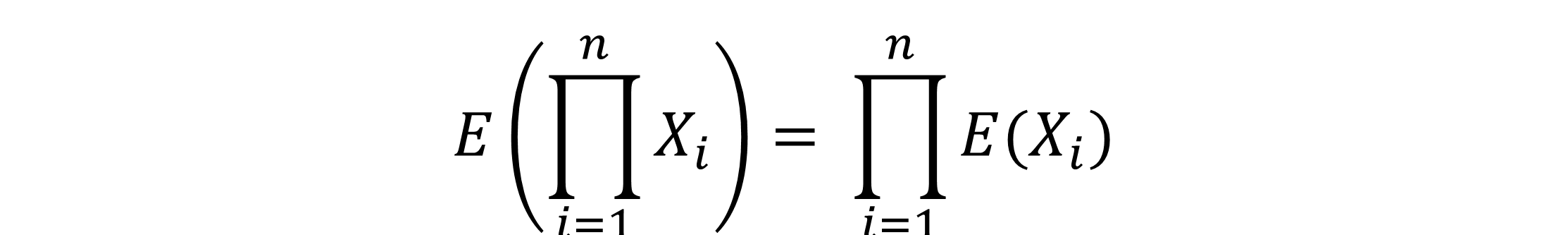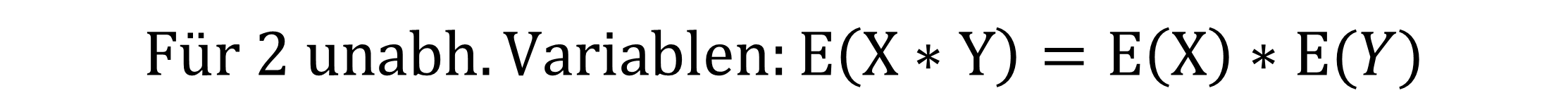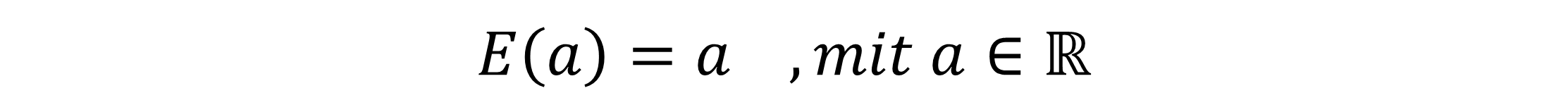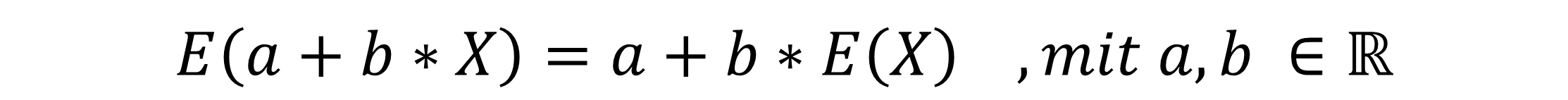Erwartungswert leichtverständlich mit Beispielen erklärt

In diesem Artikel erfährst du, was der Erwartungswert ist und wie man ihn berechnet. Das Ganze wird dir anschaulich und leicht verständlich mit Beispielen erklärt.

Abschließend noch ein Quiz, damit du kontrollieren kannst, ob du das Gelernte verstanden hast.

Los geht’s!

Erwartungswert Definition – Was ist das?

Der Erwartungswert von der Variable X ist ein Lageparameter der Verteilung von Zufallsvariablen in der Stochastik und kann für fast jede Wahrscheinlichkeitsverteilung berechnet werden. Er wird in der Mathematik mit E(X) oder dem griechischen Buchstaben μ (gesprochen “my”) abgekürzt.

Wenn du ein Zufallsexperiment unendlich oft wiederholst, zeigt dir der Erwartungswert, welchen “Mittelwert” (Durchschnitt) du langfristig erwarten kannst. Beispielsweise bei einem Würfelwurf-Experiment die Augenzahl, die du auf lange Sicht im Durchschnitt werfen wirst.

Mathematisch lässt sich der Erwartungswert von der Variablen X berechnen, indem du das arithmetische Mittel (Durchschnitt/Mittelwert) von allen Realisationen von X mit den Wahrscheinlichkeiten P dieser multiplizierst.

Wie berechnet man den Erwartungswert – Formel:

Nachdem du eine grundlegende Definition des Erwartungswertes erhalten hast, zeigen wir dir jetzt, wie du den Erwartungswert berechnen kannst. Dabei muss der Erwartungswert für diskrete und stetige Zufallsvariablen unterschieden werden.

Berechnung Erwartungswert – diskrete Zufallsvariablen

Bevor wir zur Berechnung kommen, zeigen wir dir noch einmal, was eine diskrete Zufallsvariable auszeichnet:

Wie bereits weiter oben erklärt, wird der Erwartungswert μ einer diskreten Zufallsverteilung berechnet, indem man die Summe aus der Multiplikation aller einzelnen Realisationen von x mit der individuellen Eintrittswahrscheinlichkeit P bildet.

Rechenbeispiel für diskrete Zufallsvariablen:

Um dir das Ganze zu verdeutlichen, nehmen wir unser Würfelbeispiel vom Anfang und gehen von einem handelsüblichen Würfel mit sechs Seiten aus ➔ n = 6. Dadurch das unser Würfel nicht gezinkt ist, ist die Eintrittswahrscheinlichkeit für jede Augenzahl (1-6) gleich (Gleichverteilung) und lässt sich wie folgt berechnen:

Unsere sechs Realisationen der Zufallsvariable X sind: x₁=1, x₂=2, x₃=3, x₄=4, x₅=5, x₆=6. Setzen wir nun unsere Werte in die Formel zur Berechnung des Erwartungswertes ein.

Somit können wir beim Würfeln eines normalen Würfels erwarten, dass die Augenzahl beim einmaligen Werfen 3,5 ist. Das bedeutet auch, dass der Durchschnitt aller gewürfelten Augenzahlen auf lange Sicht 3,5 beträgt, was auch nach der Häufigkeitsverteilung Sinn macht, da die beiden Zahlen in der Mitte (3, 4) am häufigsten geworfen werden.

Berechnung des Erwartungswerts bei stetigen Zufallsvariablen

Auch hier erklären wir dir noch einmal vor der Berechnung des Erwartungswertes, was eine stetige Zufallsvariable ist.

Die Berechnung des Erwartungswerts für eine stetige Zufallsvariable X erfolgt wie bei der diskreten Zufallsvariable mit dem Formen eines gewichteten arithmetischen Mittels. Jedoch wird hier ein Integral mit dem Intervall von a bis b gebildet, indem die Zufallsvariable X mit der Wahrscheinlichkeitsfunktion f(x) multipliziert wird.

Rechenbeispiel für stetige Zufallsvariablen:

Damit du das ganze nachvollziehen kannst, hier eine kleine Beispielrechnung. Stell dir vor, du wohnst in einem kleinen Dorf und der Bus, mit dem du in die Stadt fahren möchtest, fährt nur einmal in der Stunde.

Da du keine Uhr bei dir hast, weißt du nicht wann der letzte Bus abgefahren ist oder der nächste losfahren wird. Du möchtest jetzt berechnen, wie lange du im Schnitt in den nächsten 60 Minuten auf die Ankunft des Busses warten musst.

Die Wahrscheinlichkeitsfunktion ist für dieses Beispiel gleichverteilt, da die Wahrscheinlichkeit, dass der Bus innerhalb der nächsten Stunde (60 Minuten) an der Haltestelle hält, zu jedem Zeitpunkt gleich groß ist.

Diese Zufallsgröße (der Zeitpunkt) ist stetig, da er auf die kleinste Millisekunde genau angegeben werden könnte, also überabzählbar ist.Damit das nicht unübersichtlich wird, geben wir die Ankunft des Busses nur auf die Minute genau an. Die Funktion lautet für uns:

Um den Erwartungswert berechnen zu können, brauchen wir noch die Intervallgrenzen a und b unseres Integrals. Für unser Beispiel ist a=0 und b=60, weil die Möglichkeit besteht, dass der Bus genau im nächsten Moment hält (0 Minuten) oder genau vor einem Moment abgefahren ist und du jetzt für eine Stunde (60 Minuten) warten musst.

Damit haben wir jetzt alle notwendigen Teile für das Integral, um den Erwartungswert zu berechnen.

Somit beträgt der Erwartungswert 30 Minuten. Daraus kannst du schließen, dass wenn du häufig in die Stadt fahren willst und du nicht weißt wie viel Uhr es ist, du im Schnitt 30 Minuten auf deinen Bus warten musst.

Erwartungswert für verschiedene besondere Verteilungen:

Wenn du den Erwartungswert für die ein oder andere Wahrscheinlichkeitsverteilung berechnen möchtest, geht das einfacher als im letzten Abschnitt erklärt und bei einigen brauchst du nur den Wert ablesen 🙂.

Erwartungswert – Bernoulli-Verteilung

Die Bernoulli-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Sie wird auch Null-Eins-Verteilung genannt, da es für die Zufallsvariable X nur zwei mögliche Ergebnisse gibt: 0 (= Misserfolg) und 1 (= Erfolg).

Die Wahrscheinlichkeit, die den Erfolg angibt, ist P. Die Gegenwahrscheinlichkeit Q gibt an, mit wie viel Prozent es ein Misserfolg ist und lässt sich errechnen, indem man 1-P=Q berechnet.

Für die Bernoulli Verteilung ist es total einfach den Erwartungswert herauszufinden, da du in diesem Fall einfach nur die Wahrscheinlichkeit P ablesen musst, weil hier P=μ=E(x) gilt.

Erwartungswert für die Binomialverteilung

Auch die Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, wie die Bernoulli-Verteilung. Sie hat den Unterschied, dass nicht die einmalige Durchführung betrachtet wird, sondern das Zufallsexperiment n-mal wiederholt wird.

Dementsprechend lässt sich der Erwartungswert für die Binomialverteilung berechnen, indem man die Wahrscheinlichkeit P mit der Anzahl n multipliziert: μ=E(x)=P ∗ n.

Der Erwartungswert in der Normalverteilung

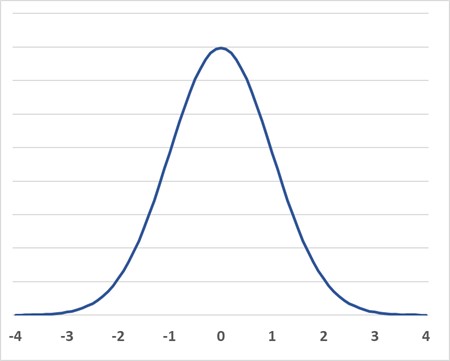
Die Dichte der Funktion ist symmetrisch um den Punkt x = μ. Dementsprechend ist der Erwartungswert auch der Median (x _0,5 = μ).

Du kannst aus einer graphischen Darstellung einer Normalverteilungsfunktion den Erwartungswert bestimmen, indem du den höchsten Punkt bestimmst.

Hier zur Erinnerung die Dichtefunktion und die Verteilungsfunktion der Normalverteilung:

Sowohl die Dichte- als auch die Verteilungsfunktion folgen immer dem gleichen Schema. Sie unterscheiden sich immer nur durch die unterschiedlichen Werte für μ und σ.

Wenn du den Erwartungswert für eine Normalverteilung angeben musst, kannst du einfach den jeweiligen μ-Wert aus der Funktion ablesen.

Der Erwartungswert und die Exponentialverteilung

Auch die Exponentialverteilung ist eine stetige Verteilung, die als Besonderheit das parameter Lamda “λ” enthält. Das λ verändert sich im Wert, der aber eine positive reelle Zahl sein muss.

Um den Erwartungswert zu berechnen musst du hier eins durch Lamda teilen: μ=E(x)=1/λ

Tabelle – Zusammenfassung Verteilungen

Vier simple Rechenregeln für Erwartungswerte:

Zum Abschluss noch vier einfache Rechenregeln, die du für dich bei der Berechnung von Erwartungswerten anwenden kannst.

1. Wenn du den Erwartungswert von der Summe von zwei oder mehr verschiedenen Zufallsvariablen hast, kannst du diese wie folgt umformen:

2. Wenn du zwei oder mehr unabhängige Zufallsvariablen hast, kannst du das Produkt dieser Erwartungswerte (Multiplikation) mit dieser Regel umformen:

3. Wenn du den Erwartungswert für eine Konstante a berechnen möchtest, ist dies immer die Konstante selbst. Eine Konstante ist eine Zahl mit einem festen Wert, der nicht variiert werden kann.

4. Wenn du einen Erwartungswert mit einer unabhängigen Zufallsvariable X und zwei Konstante a und b hast, die Element der reellen Zahlen sind, kannst du die lineare Transformation zur Umformung nutzen:

Abschlussquiz: