4,28 von 5 Sterne
Loading...
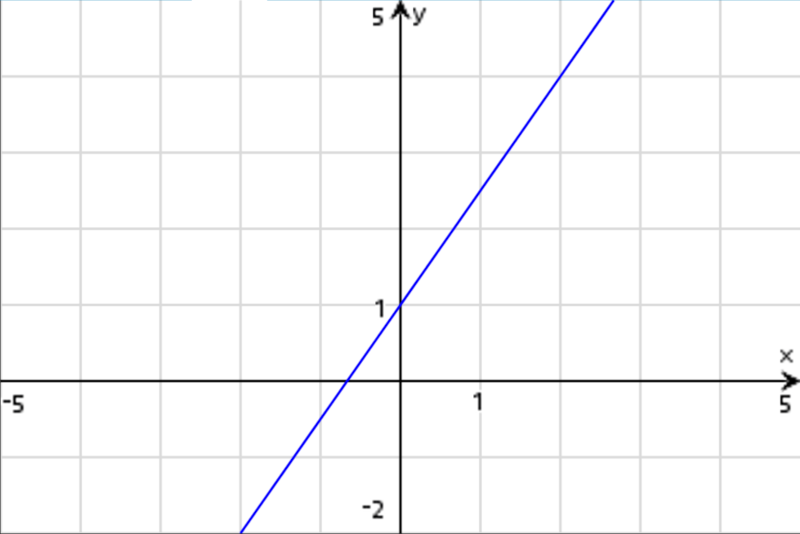
Das Thema Steigung berechnen ist ein recht einfaches mathematisches Problem. Dafür brauchst du jedoch ein paar wichtige Formeln und Infos.
Wir zeigen dir…
… was eine Steigung genau ist,
… wie du sie direkt von einem Graphen ablesen,
… aus unterschiedlichen gegebenen Werten berechnen,
… und auch selbst in ein Koordinatensystem einzeichnen kannst.
Also, schnapp dir etwas zum Mitschreiben und los geht’s!
Ein Hausdach beispielsweise muss ein bestimmtes Gefälle haben, damit das Regenwasser gut abfließen kann. Aber auch bei kleinen Heimwerker-Projekten wirst du sicherlich selbst einmal in die Situation kommen, eine Steigung auszurechnen.
Sicherlich kennst du auch das Verkehrsschild, welches ein starkes Gefälle ankündigt.
In der Mathematik ist die Steigung insb. bei der Kurvendiskussion wichtig.
Doch was hat es eigentlich mit den Begriffen Steigung, Gefälle und sogar Neigung auf sich?
Es gibt eigentlich keinen Unterschied. Auch wenn Steigung meist für einen positiven Anstieg und Gefälle für eine negative Neigung verwendet wird, ist mit Steigung alles gemeint. Die Steigung ist ein Maß für die Steilheit von Geraden.
Mathematische Form
Die Gleichung einer linearen Funktion hat die Form:
m: Steigung
n: Wert auf y-Achse
An der Funktion kannst du erkennen, wie steil der Graph steigt oder fällt:
Beispiel:
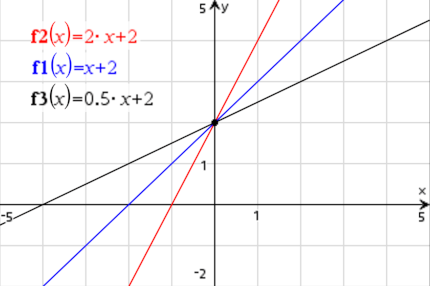
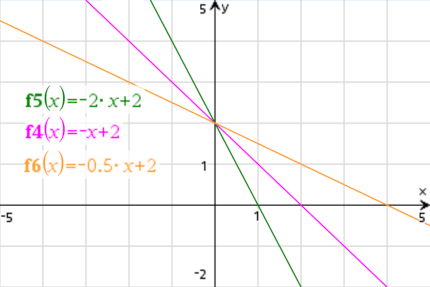
→ Links im Bild siehst du positive Steigungen und rechts im Bild sind die Funktionen fallend. Wenn du auf den Betrag “m” achtest siehst du außerdem, wie sich die einzelnen Steigungen verändern.
Steigung berechnen Formel
Für die Berechnung der Steigung gibt es keine allgemeingültige Formel. Je nach dem was gegeben und gesucht ist, gibt es unterschiedliche Herangehensweisen.
Hast du einmal die Regeln verstanden, wird dir das Bestimmen der Steigung sehr leicht fallen.
Steigung ablesen
Um die Steigung einfach ablesen zu können, muss der Funktionsgraph in einem Koordinatensystem gegeben sein. Dafür verwendest du das Steigungsdreieck.
Steigungsdreieck
Das Steigungsdreieck dient zur Veranschaulichung der Steigung einer linearen Funktion. Du beginnst immer am Schnittpunkt der Funktion mit der y-Achse (hier n = 2) und gehst so viele Kästchen bzw. Einheiten nach rechts, bis sich mit einem geraden Strich nach oben eine eindeutige Zahl ablesen lässt.
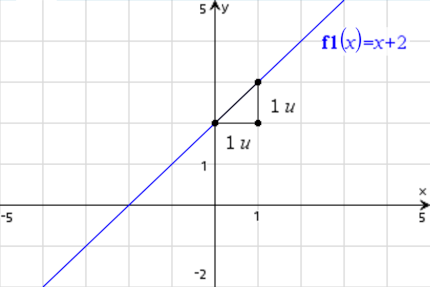
→ 1 Einheit nach rechts, 1 nach oben → Steigung m = 1
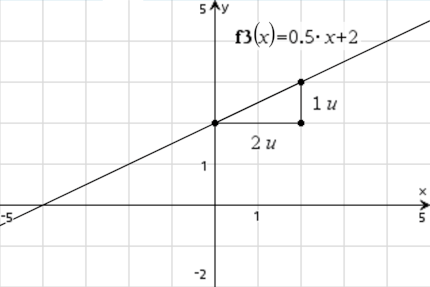
→ 2 Einheiten nach rechts, 1 nach oben → Steigung m = 0.5
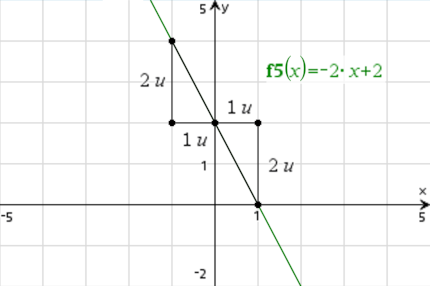
Genauso funktioniert es übrigens auch bei Graphen mit negativer Steigung. Entweder du gehst nach rechts und unten, oder nach links und oben. Das Prinzip bleibt das gleiche.
In diesem Beispiel ist die Steigung m = -2.
Steigung einer Geraden berechnen
Alternativ kannst du die Steigung auch rechnerisch bestimmen.
Nehmen wir wieder das Beispiel von oben. Ist der Graph der Funktion gegeben, musst du zwei Punkte auf dem Funktionsgraphen ablesen und diese dann in die Steigungsformel einsetzen.
Steigungsformel
Punkte \displaystyle P_{ 0 } (x_{ 0 }/y_{ 0 }) und \displaystyle P_{ 1 } (x_{ 1 }/y_{ 1 })
Steigungsformel \displaystyle m = \frac{\Delta y}{\Delta x} = \frac{ (y_{ 1 }-y_{ 0 }) }{ (x_{ 1 }-x_{ 0 }) }
Im Beispiel: \displaystyle P_{ 0 } (0/2) und \displaystyle P_{ 1 } (2/3)
\displaystyle m = \frac{3-2}{2-0}\displaystyle m = \frac{1}{2}= 0.5
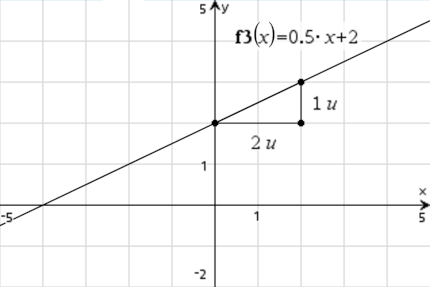
Sind allerdings schon zwei Punkte gegeben, musst du diese nicht ablesen und kannst sie direkt in die Steigungsformel einsetzen.
Steigungswinkel berechnen
Um den Steigungswinkel besser zu verstehen, klären wir erstmal, was man überhaupt unter der Angabe von Grad und Prozent bei Steigungen versteht.
Steigungen in Prozent
Erinnerst du dich noch an das Verkehrsschild?
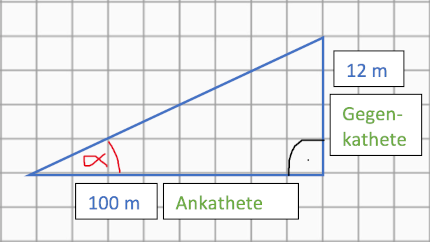
Das Schild weist auf ein Gefälle bzw. eine Steigung von 12 Prozent hin. Das bedeutet, dass pro 100 m waagerechter Strecke die Höhe um 12 m zunimmt.
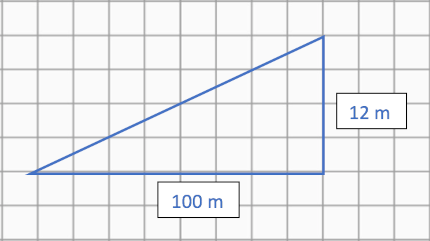
[Abbildung ist nicht verhältnismäßig]
Berechnung: \displaystyle \frac{Höhenunterschied}{waagerechte\ Strecke}=\frac{12}{100}= 12\ \%
Steigungen in Grad
Die Steigung kann aber auch über den Steigungswinkel α angegeben werden. Um den Winkel zu berechnen, brauchen wir die Trigonometrie.
Formel: \displaystyle tan (\alpha)=\frac{ Gegenkathete }{ Ankathete }=m
Im Beispiel:
\displaystyle tan (\alpha)=\frac{ 12 }{ 100 }
Wenn wir jetzt aber den Winkel bestimmen wollen, müssen wir nach α umstellen und den arctan (oft auch \displaystyle tan^{ -1 }) berechnen:
\displaystyle \alpha= arctan(\frac{ 12 }{ 100 })= 6.84°
Allg. Formel: \displaystyle \alpha=arctan(\frac{ Höhenunterschied }{ waagerechte\ Strecke })= arctan (m)
Ist die Steigung negativ, musst du 180 Grad zu dem Ergebnis hinzurechnen, da du lediglich den kleineren negativen Winkel berechnest!
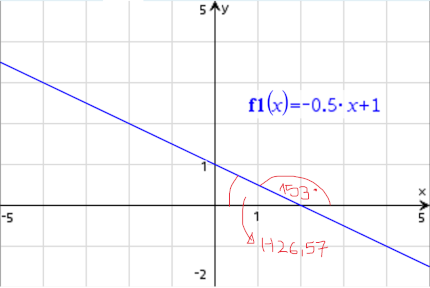
Beispiel:
\displaystyle f(x) = -0.5x + 1
→ \displaystyle arctan (m) = arctan(- 0.5) = -26.57°
\displaystyle + 180° \approx 153°
Sonderfälle:
Gerade parallel zur x-Achse → α = 0 Grad
Gerade parallel zur y-Achse → α = 90 Grad
Prozent – Grad Umrechnung
Steigungswinkel (°) = \displaystyle arctan(\frac{ Steigung\ (\%) }{ 100 })
Steigung (%) = \displaystyle tan( Steigungswinkel\ (°)) * 100
Gerade mit Steigungsdreieck zeichnen
Hast du die Aufgabe, eine lineare Funktion bzw. Gerade mit vorgegebener Funktionsgleichung in ein Koordinatensystem zu zeichnen, hilft dir das Steigungsdreieck.
Gehe wie folgt vor:
Aufgaben mit Lösungen – Jetzt bist du dran
Um das Gelernte anzuwenden, haben wir noch je eine Aufgabe zu der jeweiligen Aufgabenstellung.
Mach dir erst Gedanken bzw. Notizen und überprüfe dann deine Lösungen.
Die Steigung kannst du wie abgebildet mit dem Steigungsdreieck bestimmen. Die Funktionsgleichung erhälst du durch einsetzen von n und m.
y = mx + n
m = 1.5
n = 1
y = 1.5x + 1
\displaystyle P_{ 0 } (0/2) und \displaystyle P_{ 1 } (1/4)
\displaystyle P_{ 0 } (x_{ 0 }/y_{ 0 }) und \displaystyle P_{ 1 } (x_{ 1 }/y_{ 1 })
\displaystyle m = \frac{\Delta y}{\Delta x} = \frac{ (y_{ 1 }-y_{ 0 }) }{ (x_{ 1 }-x_{ 0 }) }\displaystyle m = \frac{ 4-2 }{ 1-0 } = \frac{ 2 }{ 1 }=2
Steigung von 25 Prozent
Eine Steigung von 25 % bedeutet einen Höhenunterschied von 25 m bei 100 m waagerechter Strecke.
\displaystyle tan (\alpha)=\frac{ Gegenkathete }{ Ankathete }\displaystyle \alpha=arctan(\frac{ Gegenkathete }{ Ankathete })
\displaystyle \alpha=arctan(\frac{ 25 }{ 100 })
\displaystyle \alpha=14.04°
FAQ Steigung berechnen
Die Steigung wird mit der Steigungsformel berechnet.
Diese lautet: \displaystyle m = \frac{\Delta y}{\Delta x} = \frac{ (y_{ 1 }-y_{ 0 }) }{ (x_{ 1 }-x_{ 0 }) }=\frac{Höhenunterschied}{waagerechte\ Strecke}
Das bedeutet, dass auf einer waagerechten Strecke von 100 m eine Höhe von 10 m überwunden wird.
100 % Steigung entsprechen 45 Grad. Kurze Erklärung: Höhen- und Längenunterschied sind je 100, sodass eine Gerade im Quadrat winkelhalbierend ist und einen Winkel von 45 Grad einschließt.
Ja. Bei genau 45 Grad ist die Steigung 100 %. Alles darüber hinaus stellt eine höhere Steigung als 100 % dar.
Nicht nur Graphen steigen, sondern auch deine Noten, wenn du beim Nachhilfe-Team dabei bist!
93% unserer Nachhilfeschüler haben sich nach mind. 4 Einheiten bei uns um 1-2 Noten verbessert!
Egal ob in Berlin, Köln oder München – wir sind überall vertreten und helfen gern!
Nutze jetzt auch unser Online-Programm und starte durch!
Außerdem würden wir uns sehr über deine Bewertung freuen! Damit tust du uns einen großen Gefallen 😉
4,28 von 5 SterneLoading...
Kennst du schon unsere Beiträge zur Zinsrechnung, Trigonometrie und zur pq-Formel?