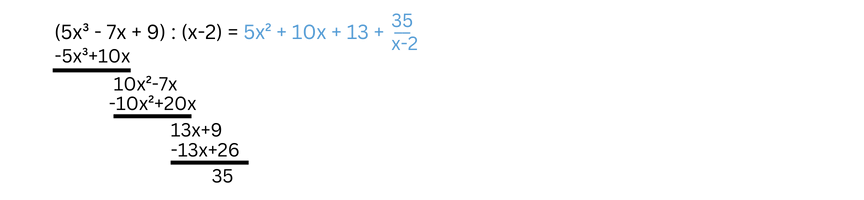Polynomdivision – Einfache Schritt-für-Schritt Anleitung

In deinem Mathe Unterricht wurde das Thema Polynomdivision behandelt, aber du verstehst nicht wirklich, wie es funktioniert und was das eigentlich bringen soll?

Keine Sorge, in diesem Artikel erklären wir dir ganz einfach anhand von Beispielen, wie du die Polynomdivision korrekt benutzt und weshalb sie verwendet wird. Außerdem kannst du dich direkt an Übungsaufgaben messen und wir zeigen dir, was es mit dem schriftlichen Dividieren aus der Grundschule zu tun hat.

Legen wir sofort los!

Polynomdivision – einfache Erklärung

Was ist die Polynomdivision eigentlich? Dafür müssen wir zuerst klären, was Polynome denn sind. Polynome sind mehrliedige Terme, die Potenzen enthalten, so wie diese hier :

f(x) = 4x² + 2x – 10
g(x) = x-2

Die Polynomdivision ist jetzt also, wie der Name sagt, eine Division von diesen beiden Termen. Du kannst damit also etwa sowas hier ausrechnen:

Wie du auf diese Lösung kommst, werden wir dir gleich Schritt für Schritt erklären. Es hat also große Ähnlichkeit mit dem schriftlichen Dividieren, wie du es schon aus der Grundschule kennst.

Polynomdivision  an Beispielen simpel erklärt

Um dieses Verfahren durchzuführen, braucht man mehrere Schritte. Lass dich davon allerdings nicht abschrecken, denn obwohl es viel aussehen mag, ist es dennoch überhaupt nicht kompliziert.

Im ersten Schritt überlegen wir uns, womit wir x multiplizieren müssen, um 4x² zu erhalten. Die Antwort ist natürlich 4x, denn 4x × x = 4x². Diese Antwort schreiben wir als ersten Teil der Lösung rechts neben das =.

(4x² + 2x – 10) : (x-2) = 4x

Jetzt multiplizieren wir das gefundene 4x mit dem Divisor, also x-2. Das Ergebnis davon ist 4x × (x-2) = 4x² – 8x. Das schreiben wir nun unter das erste Polynom, wie bei der schriftlichen Division müssen wir davor aber noch ein Minus-Zeichen setzen sowie einen Strich.

Jetzt ziehen wir (4x²-8x) von dem Polynom darüber ab und schreiben das Ergebnis unter den Strich.

Das kann man bis jetzt als den ersten Durchgang bezeichnen. Wir wiederholen die Schritte 1 bis 3 mit dem Term, der übrig bleibt: 10x-10. Wir fragen uns erneut, womit man x multiplizieren muss, um 10x zu erhalten. Die Antwort, 10, schreiben wir auf die Ergebnisseite rechts.

Wir multiplizieren die 10 mit (x-2) und schreiben das Ergebnis unter das Restpolynom. Minus Zeichen und Strich darunter nicht vergessen!

Wir ziehen wieder das Restpolynom ab und schreiben das Ergebnis unter den Strich.

Dieser Durchgang wäre damit auch geschafft. Jetzt fangen wir wieder von vorne an und überlegen uns, womit wir x multiplizieren müssen, um auf 10 zu kommen. Wir sehen, dass das nicht geht. Somit sind wir am Ende der Polynomdivision angekommen und müssen nur noch den Rest zum Ergebnis schreiben. Das wäre 10:(x-2).

Polynomdivision mit Rest – das solltest du wissen!

Unsere Beispielaufgabe hat jetzt einen Rest – also die Rechnung geht nicht “glatt” auf und deswegen müssen wir 10/(x-2) hinten dran hängen. Das ist nicht schlimm und wird in den meisten Fällen so auftreten. Allerdings gibt es auch Aufgaben, die ohne Rest auskommen. Diesen Fall werden wir uns weiter unten in den Übungsaufgaben noch anschauen.

Polynomdivision Nullstellen berechnen

Mit Hilfe der Polynomdivision können wir Nullstellen von Funktionen berechnen, die nicht so einfach mit der pq-Formel zu ermitteln sind. Also etwa x^3-3x²-6x+8. Nun muss die Voraussetzung sein, dass du bereits eine Nullstelle dieser Funktion kennst. Es gibt eine Methode, in der wir eine Nullstelle sozusagen “erraten” können. Und zwar mit den Teilern des absoluten Gliedes.

Das absolute Glied einer Funktion ist immer der Zahlenwert, an dem kein x-Wert angegliedert ist, hier also die 8. Die Teiler von 8 sind 1,2,4, -1, -2 und -4. Jetzt führen wir nach und nach die Polynomdivision durch, bis wir eine Lösung ohne Rest erhalten und haben somit eine Nullstelle der Funktion. Wenn wir das ganze mit der obigen Funktion und dem Teiler 1 benutzen, erhalten wir dieses Ergebnis:

Somit ist eine Nullstelle also 1. Somit können wir nun die Lösung der Polynomdivision nehmen, also x²-2x-8 und dort einfach die PQ-Formel anwenden, um auf die weiteren Nullstellen zu kommen.

Polynomdivision Aufgaben zum Nachrechnen

Wir haben ja schon bei den Nullstellen gesehen, dass es Lösungen ohne Rest gibt. Im Folgenden haben wir dir eine Aufgabe gestellt, bei der dies auch der Fall ist. Versuche, sie selbst zu lösen und klicke auf die Lösung, um diese sowie den Rechenweg zu sehen.

Polynomdivision Rechner

Hoffentlich kannst du jetzt fehlerfrei die Polynomdivision durchführen! Falls es doch mal schnell gehen muss oder du deine Lösung kontrollieren willst, kannst du das ganz einfach über diese Website machen : Matheretter

Wir hoffen, dass wir dir die Polynomdivision anschaulich beibringen konnten. Hast du noch Fragen? Dann stell sie gerne in den Kommentaren.

Falls du weitere Hilfe zu Mathe-Themen benötigst, dann schau dich doch gerne auf unserer Website um. Wir haben Erklärungen zu vielen verschiedenen Matheproblemen, die du dir schnell und unkompliziert anschauen kannst.

Benötigst du doch noch ein wenig mehr Unterstützung? Unser Nachhilfeangebot wird dir dabei weiterhelfen! Und das Beste: Du kannst es sogar online in Anspruch nehmen. Unsere qualifizierten Nachhilfelehrer werden dir mit Rat und Tat bei all deinen Fragen zur Seite stehen.