Brüche kürzen – schnell und leicht erklärt

3,67 von 5 SterneLoading...

Du sollst im Matheunterricht Brüche kürzen, aber verstehst nur Bahnhof? Dann bist du hier richtig! Wir erklären dir anhand von Beispielen, wie man Brüche problemlos kürzt.

Lass uns beginnen…

Was ist ein Bruch?

Brüche bestehen aus einem Zähler und einem Nenner, die durch einen horizontalen Bruchstrich getrennt sind. Die Zahl über dem Bruchstrich heißt Zähler, die Zahl unter dem Bruchstrich Nenner. Der Bruchstrich zwischen Zähler und Nenner bedeutet, dass der Zähler durch den Nenner geteilt werden soll (Division).

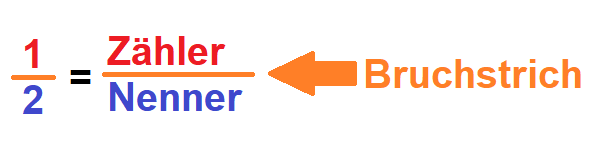
Brüche kürzen – Erklärung

Brüche zu kürzen heißt Brüche zu vereinfachen oder zu verkleinern. Du kannst Brüche kürzen, indem du Zähler und Nenner jeweils durch die gleiche Zahl dividierst.

Damit du verstehst wie das Kürzen von Brüchen funktioniert, schauen wir uns das folgende Beispiel anhand einer Pizza an:

Die linke Pizza schneiden wir in 4 Stücke, die alle gleich groß sind.

2 der 4 Stücke werden verspeist, sodass ein Bruch von \displaystyle \frac{\color{red}{2}}{\color{blue}{4}} verbleibt. Da 2 von 4 Stücke noch übrig sind, bleibt die halbe Pizza übrig.

Rechts siehst du aber nur 1 von 2 Stücken der Pizza, also \displaystyle \frac{\color{red}{1}}{\color{blue}{2}}.

Zwar hat sich an der Menge der Pizza nichts geändert. Trotzdem werden zwei verschiedene Brüche verwendet, die beide dasselbe meinen.

➡️ Das hat zur Folge, dass zwei Viertel Stücke einer Pizza und eine halbe Pizza gleich viel sind.

Brüche kürzen – Beispiel

Nachdem du jetzt gesehen hast, was ein Bruch ist und was Brüche kürzen bedeutet, lernst du in diesem Kapitel, wie man einen Bruch genau kürzt. Betrachten wir nun das folgende Beispiel.

Beispiel: Du hast den Bruch \displaystyle \frac{\color{red}{14}}{\color{blue}{36}}und sollst ihn mit 2 kürzen.

Du teilst Zähler und Nenner durch 2. Im Zähler rechnest du 14 : 2 und im Nenner 36 : 2. Du erhältst den gekürzten Bruch.

\displaystyle \frac{\color{red}{14}}{\color{blue}{36}} = \displaystyle \frac{\color{red}{14}\color{green}:2}{\color{blue}{36}\color{green}:2} = \displaystyle \frac{\color{red}{7}}{\color{blue}{18}}

Lassen sich sowohl Zähler als auch Nenner durch dieselbe Zahl teilen, so ändert sich der Wert des gekürzten Bruches nicht.

Kürzungszahl überlegen

Die Kürzungszahl ist die Zahl, bei der man Zähler und Nenner durch dieselbe Zahl dividiert. Bevor du einen Bruch kürzt, überlegst du dir durch welche Zahl Zähler und Nenner teilbar sind. Im Zähler und im Nenner darf keine Kommazahl (kein Rest) stehen.

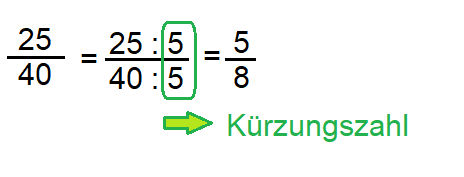
Damit du das besser verstehst, kannst du dir das Beispiel anschauen.

Beispiel: Wir haben den Bruch \displaystyle \frac{\color{red}{5}}{\color{blue}{10}} und sollen kürzen.

Beispielsweise kannst du den Bruch nicht mit 2 kürzen, da 5 nicht durch 2 teilbar ist und du im Zähler eine Kommazahl erhältst. Deshalb überlegst du dir eine andere Kürzungszahl.

\displaystyle \frac{\color{red}{5}}{\color{blue}{10}} = \displaystyle \frac{\color{red}{5}\color{green}:2}{\color{blue}{10}\color{green}:2} = \displaystyle \frac{\color{red}{2,5}}{\color{blue}{5}}

Den Bruch kannst du mit 5 kürzen, da 5 und 10 durch 5 teilbar sind. Wenn du im Zähler 5 durch 5 teilst, bekommst du eine 1. Im Nenner erhältst du eine 2, da 10 durch 5 teilbar ist.

\displaystyle \frac{\color{red}{5}}{\color{blue}{10}} = \displaystyle \frac{\color{red}{5}\color{green}:5}{\color{blue}{10}\color{green}:5} = \displaystyle \frac{\color{red}{1}}{\color{blue}{2}}

Die Kürzungszahl ist somit die 5.

Brüche vollständig kürzen

Das Ziel des Kürzens besteht darin, den Bruch in eine Form zu bringen, dass dieser nicht weiter gekürzt werden kann. Das ist dann der Fall, wenn der Bruch nicht mehr weiter teilbar ist. Dann spricht man davon, dass der Bruch vollständig gekürzt ist.

Im vorherigen Abschnitt haben wir bereits gelernt, wie man einen Bruch kürzt, zum Beispiel:

\displaystyle \frac{\color{red}{16}}{\color{blue}{36}} = \displaystyle \frac{\color{red}{16}\color{green}:2}{\color{blue}{36}\color{green}:2} = \displaystyle \frac{\color{red}{8}}{\color{blue}{18}}

An dem Bruch \displaystyle \frac{\color{red}{8}}{\color{blue}{18}} erkennen wir jedoch, dass es sich nochmals kürzen lässt:

\displaystyle \frac{\color{red}{8}}{\color{blue}{18}} = \displaystyle \frac{\color{red}{8}\color{green}:2}{\color{blue}{18}\color{green}:2} = \displaystyle \frac{\color{red}{4}}{\color{blue}{9}}

Wir stellen fest, dass wir normalerweise gleich mit der Zahl 4 vollständig kürzen können:

\displaystyle \frac{\color{red}{16}}{\color{blue}{36}} = \displaystyle \frac{\color{red}{16}\color{green}:4}{\color{blue}{36}\color{green}:4} = \displaystyle \frac{\color{red}{4}}{\color{blue}{9}}

Der Grund für das Kürzen ist, dass die kleineren Zahlen im Zähler und Nenner ein leichteres Rechnen ermöglichen. Zudem ist der Rechenweg übersichtlicher und strukturierter.

Brüche kürzen mit dem größten gemeinsamen Teiler – Schritt für Schritt

Um Brüche in die vollständig gekürzte Form zu bringen, kann hierbei der größte gemeinsame Teiler (ggT) von Zähler und Nenner helfen. Mithilfe des ggT lässt sich der Bruch so weit wie möglich kürzen. Als Teiler bezeichnet man all die Zahlen, die durch eine Zahl geteilt werden können, ohne dass ein Restwert verbleibt.

Beispiel: Der Bruch \displaystyle \frac{\color{red}{18}}{\color{blue}{24}} soll so weit wie möglich gekürzt werden.

1. Zunächst schreibst du alle Teiler vom Zähler auf, also all die Zahlen, die durch 18 teilbar sind. Dasselbe Spiel macht man mit dem Nenner 24. Beispielsweise ist die 4 kein Teiler von 18, da 18 : 4 = 4,5 sind und ein Rest übrig bleibt. Hingegen ist die 3 ein Teiler von 18, da 18 : 3 = 6 ist und kein Rest übrig bleibt.

Teiler von 18 {1,2,3,6,9}

Teiler von 24 {1,2,3,4,6,8,12}

---

2. Anschließend suchst du in den beiden geschweiften Klammern die größte Zahl heraus, also den größten gemeinsamen Teiler von 18 und 24. In dem Fall ist es die Zahl 6.

Teiler von 18 {1,2,3,6,9}

Teiler von 24 {1,2,3,4,6,8,12}

---

3. Der Bruch kann mit der 6 vereinfacht werden.

\displaystyle \frac{\color{red}{18}}{\color{blue}{24}} = \displaystyle \frac{\color{red}{18}\color{green}:6}{\color{blue}{24}\color{green}:6} = \displaystyle \frac{\color{red}{3}}{\color{blue}{4}}

Brüche kürzen mit der Primfaktorzerlegung – Schritt für Schritt

Eine andere Methode, um Brüche vollständig zu kürzen ist die Primfaktorzerlegung. Bei einer Primzahl handelt es sich um eine natürliche Zahl. Diese ist nur durch sich selbst und durch 1 teilbar, wobei die 1 selbst keine Primzahl ist. Die ersten Primzahlen lauten 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31.

Beispiel: Mit Hilfe der Primfaktorzerlegung sollst du den Bruch \displaystyle \frac{\color{red}{16}}{\color{blue}{24}} vollständig kürzen.

1. Zähler und Nenner werden in Primfaktoren zerlegt. Die Zahl 16 im Zähler lässt sich durch die Primzahl 2 zerlegen. Dadurch entsteht die Multiplikation von 2 mal 8. Die 8 wiederum lässt sich ebenfalls durch die 2 zerlegen. Daher entsteht die Multiplikation von 2 mal 4. Die 4 kannst du nun auch noch einmal zerlegen in 2 × 2.

  16 = 2 × 8

               = 2 × 2 × 4

                       = 2 × 2 × 2 × 2

---

2. Bei der Zahl 24 im Nenner  lässt sich dieses Spiel wiederholen. Die Zahl 24 lässt sich ebenfalls mit 2 kürzen und man erhält die Kombination aus 2 × 12.  Die 12 kann mit der 2 weiter gekürzt werden und man erhält die Multiplikation 2 × 6. Die 6 lässt sich zerlegen in 2 × 3.

        24 = 2 × 12

                   = 2 × 2 × 6

                          = 2 × 2 × 2 × 3

---

3. Im Zähler und Nenner können wir die gleichen Zahlen durchstreichen und das Ergebnis berechnen. Im Zähler und Nenner können wir die 2 dreimal wegstreichen. Die Zahl 2 bleibt im Zähler übrig und im Nenner erhält man die Zahl 3.

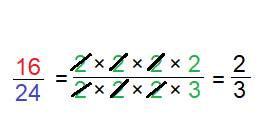
Brüche kürzen und erweitern

Brüche kürzen heißt Zähler und Nenner durch die gleiche Zahl dividieren. Beim Erweitern von Brüchen multiplizierst du Zähler und Nenner durch dieselbe Zahl.

Wie beim Kürzen bleibt der vom Bruch dargestellte Wert unverändert. Erweitern ist das Gegenteil von Kürzen.

Beispiel: Du sollst den Bruch \displaystyle \frac{\color{red}{2}}{\color{blue}{5}}mit der 5 erweitern.

Du multiplizierst Zähler und Nenner mit der 5. Im Zähler rechnest du 2 × 5 und im Nenner 5 × 5. Damit erhältst du den erweiterten Bruch.

\displaystyle \frac{\color{red}{2}}{\color{blue}{5}} = \displaystyle \frac{\color{red}{2}\color{black} × \color{green}5}{\color{blue}{5}\color{black} ×\color{green}5} = \displaystyle \frac{\color{red}{10}}{\color{blue}{25}}

Brüche kürzen Aufgaben

Und jetzt bist du an der Reihe! Hier findest du Aufgaben, die dir beim Üben helfen. Anschließend findest du zu den Übungsaufgaben die passenden Lösungen. Klicke einfach auf die Links und schon öffnen sich die Dateien.

Viel Erfolg!

Brüche kürzen – Aufgaben

Brüche kürzen – Lösungen

FAQ