Du wirst im Matheunterricht nicht daran vorbeikommen, dass du einen Schnittpunkt berechnen sollst. Es ist also ratsam, alles darüber zu wissen und die Berechnung zu beherrschen. In diesem Artikel lernst du, was ein Schnittpunkt ist und wie du ihn in verschiedenen Fällen ermitteln kannst.
Los geht’s…
Schnittpunkt berechnen – wie geht das?
Damit du den Punkt findest, in dem sich zwei Graphen schneiden, musst du zuerst die dazugehörigen Funktionen gleichsetzen. Genau an diesem Schnittpunkt haben die Funktionen nämlich den gleichen Wert.
Als nächsten Schritt löst du diese Gleichung nach x auf und hast so den x-Wert des Schnittpunktes. Setzt du diesen Wert in eine der beiden Funktionen ein, erhältst du den y-Wert und so den kompletten Schnittpunkt.
Beispiel:
f(x) = 12x+20
g(x) = 35-18x
setze f(x) = g(x) und löse nach x auf:
12x+20 = 35-18x
30x = 15
x = 0,5
setze x = 0,5 in f(x) oder g(x) ein
→ Schnittpunkt bei (0,5/26)
Wie liest man den Schnittpunkt ab?
Wenn du ein zweidimensionales Koordinatensystem mit zwei Graphen graphisch vor dir hast, kannst du den Punkt, in dem sich die Graphen treffen auch ermitteln, ohne den Schnittpunkt berechnen zu müssen.
Dazu gehst du vom Schnittpunkt jeweils ganz gerade zur x- und zur y-Achse und liest den entsprechenden Wert ab.
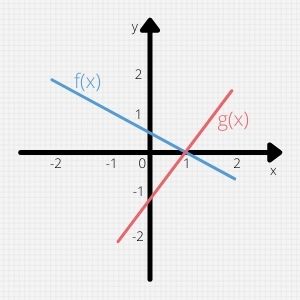
In unserer Grafik siehst du sofort, dass der Schnittpunkt von f(x) und g(x) bei dem Punkt (1/0) liegt.
Diese Methode hat jedoch den Nachteil, dass du den Punkt eventuell nicht ganz exakt ablesen kannst, wenn das Koordinatensystem nicht genau gezeichnet ist.
Schnittpunkt berechnen bei linearen Funktionen
Lineare Funktionen (m*x+b) können nur einen Schnittpunkt besitzen, wenn sie unterschiedliche Steigungen haben. Sind die Steigungen jedoch gleich, verlaufen die Geraden der Funktionen parallel zueinander und treffen sich nie.
Beispiel für parallele Geraden:
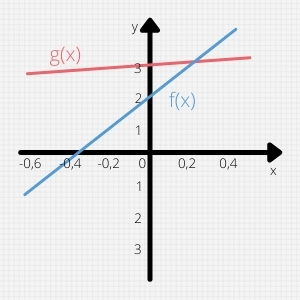
f(x) = 15x+8
g(x) = 15x+3
Beide Funktionen haben die Steigung +15, deshalb verlaufen sie parallel.
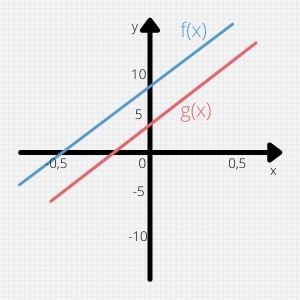
Beispiel für nicht-parallele Geraden:
f(x) = 5x+2
g(x) = 3+x
5x+2 = 3+x
4x = 1
x = 0,25
f(0,25) = 3,25
→ Schnittpunkt bei (0,25/3,25)
Wie viele Schnittpunkte können zwei lineare Funktionen haben?
Eine lineare Funktion hat überall die gleiche Steigung. Deshalb verlaufen die Graphen von zwei linearen Funktionen immer gerade. Das führt dazu, dass zwei lineare Funktionen höchstens einen Schnittpunkt haben können.
Wenn sie sich einmal geschnitten haben, werden sie sich nie wieder annähern.
Zwei Geraden haben also entweder keinen oder einen Schnittpunkt.
Erhältst du beim Gleichsetzen der Funktionen eine immer wahre Aussage z.B. 15 = 15, sind die Funktionen identisch und liegen perfekt aufeinander. Sie haben dann unendlich viele gemeinsame Punkte, jedoch keinen Schnittpunkt.
Wo sich quadratische Funktionen schneiden
Quadratische Funktionen haben die Form: a*x²+b*x+c
Auch hier kannst du wie oben den Schnittpunkt berechnen:
- Funktionen gleichsetzen
- Nach x auflösen
- x in eine der Funktionen einsetzen
- y-Wert bestimmen
- Schnittpunkt benennen
Bei quadratischen Funktionen erfordert jedoch die Auflösung nach x noch einen Schritt mehr.
Beispiel:
f(x) = x²+10x-8
g(x) = 5x²-13
f(x) = g(x)
x²+10x-8 = 5x²-13
x²-5x²+10x = -13+8
-4x²+10x = -5
Um hier jetzt die Gleichung zu lösen, benötigen wir die pq-Formel. Diese lautet:
Sie kann bei einer quadratischen Funktion der Form x²+px+q = 0 angewendet werden. Wir müssen unsere Funktion also erstmal in diese Funktion umwandeln.
-4x²+10x = -5
-4x²+10x+5 = 0
x²-2,5x-1,25 = 0
-> p = -2,5; q = -1,25
Jetzt setzen wir p und q in die Formel ein und erhalten:
x₁ = 2,927 und x₂ = -0,427
f(2,927) = 29,837 → erster Schnittpunkt bei (2,927/29,837)
f(-0,427) = -12,088 → zweiter Schnittpunkt bei (-0,427/-12,088)
Lineare und quadratische Funktion – schneiden sie sich?
Bei einer linearen und einer quadratischen Funktion kannst du auch ganz einfach den Schnittpunkt berechnen. Der Vorgang ist der gleiche wie oben. Du setzt zuerst die Funktionen gleich, löst nach x auf und kannst so den y-Wert und damit den Schnittpunkt oder die Schnittpunkte bestimmen.
Beispiel:
f(x)= 3x²+12x-5
g(x) = 16+9x
f(x) = g(x)
3x²+12x-5 = 16+9x
3x²+3x-21 = 0
x²+x-7 = 0
Auch hier kannst du wieder die pq-Formel anwenden:
p = 1; q = -7
-> x₁ = 2,193
-> x₂ = -3,193
f(2,193) = 35,744 → erster Schnittpunkt bei (2,19/35,74)
f(-3,193) = -12,73 → zweiter Schnittpunkt bei (-3,193/-12,73)
Schnittpunkt berechnen bei Parabel und Gerade
Parabeln und Geraden können sich in keinem, einem oder zwei Punkten schneiden.
Da eine Parabel eine quadratische Form (a*x²+b*x+c) hat, ist hier das Vorgehen das gleiche wie im vorherigen Punkt.
Du kannst hier also einfach bei einer quadratischen und einer linearen Funktion den Schnittpunkt berechnen.
Vektoren und ihre Schnittpunkte
Wir erklären dir, wie du den Schnittpunkt berechnen kannst, wenn du zwei Vektoren hast. Den Vorgang zeigen wir dir an einem Beispiel.
Du hast zu Beginn zwei Geraden mit den Vektoren:
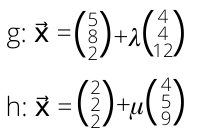
Der erste Schritt ist nun, zu checken, ob die Richtungsvektoren, also die Vektoren mit ? oder ? in den einzelnen Geraden jeweils Vielfachen voneinander sind.
Dafür testest du, ob es ein x gibt, mit dem man den einen Richtungsvektor multiplizieren könnte, um auf den anderen zu kommen.
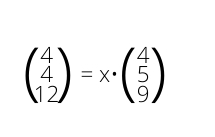
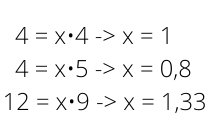
Bei unseren Geraden ist das nicht der Fall, die x sind nicht gleich. Die Geraden sind also linear unabhängig. Das heißt, sie sind entweder windschief oder schneiden sich.
Nun überprüfen wir, ob es einen Schnittpunkt gibt. Dazu müssen wir ? und ? bestimmen. Dies tun wir, indem wir beide Geraden gleichsetzen und in ein Gleichungssystem mit drei Zeilen umwandeln.
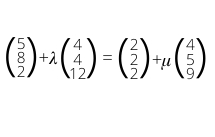
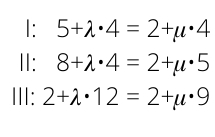
Jetzt lösen wir die ersten beiden Zeilen nach ? auf und setzen II in I ein:
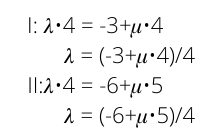

So können wir ? ausrechnen. Dieses ? setzen wir in II ein und erhalten auch ?.
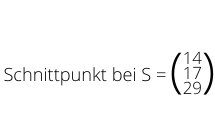
Mit der dritten Zeile, die wir bisher noch gar nicht gebraucht haben, überprüfen wir unser ? und ?. Wenn wir beide Zahlen einsetzen und ein wahres Ergebnis (z.B. 5 = 5) erhalten, haben die beiden Geraden einen Schnittpunkt.


Diesen Schnittpunkt erhalten wir ganz einfach, wenn wir jetzt ? oder ? in g bzw. h einsetzen.
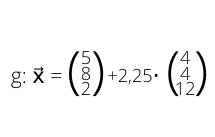
Schnittpunkt berechnen – Aufgaben mit Lösung
Bei diesen Aufgaben sind immer die Funktionen f(x) und g(x) vorgegeben und du sollst den/die Schnittpunkt/e der Funktionen bestimmen.
S = (-74|-1883)
S1 = (-0.06|-1.677) und S2 = (0.214|19.677)
S = (12.948|90.381)
S1 = (-25.454|11.546) und S2 = (1.454|38.454)
Es gibt keinen Schnittpunkt weil beide Geraden die gleiche Steigung haben (-8). Die Geraden verlaufen parallel.
Schnittpunkte – FAQ
Was ist ein Schnittpunkt?
Ein Schnittpunkt ist eine Stelle, an der sich Graphen schneiden.
Wie viele Schnittpunkte können zwei Graphen haben?
Zwei Graphen können maximal einen Schnittpunkt haben.
Welche Formel benötigt man bei der Schnittpunktberechnung von Quadratischen Funktionen?
Die p-q Formel.
Du möchtest noch tiefer in die Mathematik einsteigen?
Unser Nachhilfe-Team bietet in vielen Städten Deutschlands, wie München, Köln oder Berlin erfolgssichere Mathe Nachhilfe an.
Du möchtest noch flexibler sein? Unser Online-Programm garantiert dir genau das! Und du sparst sogar zusätzliche Anfahrtskosten 😉
Schau doch mal unverbindlich vorbei!

