- Zum einen kannst du beide Funktionen zeichnen und so den Schnittpunkt in deiner Zeichnung ablesen.
- Das Problem bei diesem Verfahren ist, dass der Schnittpunkt nur selten direkt auf einem Kästchen liegt, sodass du ihn direkt ablesen kannst.
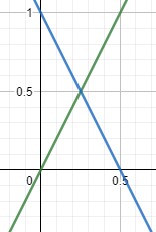
- Zum anderen kannst du den Schnittpunkt rechnerisch bestimmen.
- Dieser Weg liefert dir immer das richtige Ergebnis, auch wenn du den Schnittpunkt beim Zeichnen nicht direkt ablesen kannst.
- Deshalb konzentrieren wir uns hier auf die rechnerische Bestimmung des Schnittpunkts.
- Wir berechnen jetzt den Wert für x.
- Dazu lösen wir das Gleichungssystem so auf, dass x allein auf der einen Seite steht und alle Zahlen auf der anderen Seite stehen.
- Damit haben wir die x-Koordinate des Schnittpunkts bestimmt.
Schritt 4: Einsetzen
- Als Nächstes setzen wir den x-Wert in eine der beiden Funktionen ein, um den y-Wert zu erhalten.
- Dabei ist es egal, in welche Gleichung du den x-Wert einsetzt.
Schritt 5: Gegenprobe
- Im letzten Schritt überprüfen wir, ob wir alles richtig gerechnet haben.
- Dazu setzen wir den x-Wert noch in die andere Geradengleichung ein.
- Wenn das gleiche Ergebnis herauskommt, haben wir alles richtig gerechnet.
Schnittpunkt bestimmen – Beispielaufgaben
Aufgabe 1
Bestimme den Schnittpunkt folgender Geraden:
f(x)= 5*x + 2 (grün)
g(x) = x + 3 (blau)
Lösung Aufgabe 1
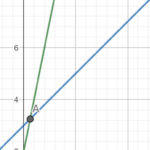
Den Schnittpunkt dieser beiden Geraden können wir grafisch nicht genau ablesen, deshalb bestimmen wir den Schnittpunkt rechnerisch.
Schritt 1: Die Steigung der beiden Funktionen betrachten
Die Steigung von f(x) beträgt 5 und die Steigung von g(x) beträgt 1. Da diese beiden Zahlen ungleich sind, besitzen die Geraden einen Schnittpunkt.
Schritt 2: Beide Gleichungen gleichsetzen
f(x) = g(x)
5*x + 2 = x + 3
Schritt 3: Gleichungssystem auflösen
5*x + 2 = x + 3 | x abziehen
4*x + 2 = 3 | 2 abziehen
4*x = 1 | durch 4 teilen
x = 0,25
Der x-Wert des Schnittpunkts lautet 0,25.
Schritt 4: Einsetzen
Nun setzen wir den x-Wert in die Geradengleichung f(x) ein.
f(x) = 5*0,25 + 2 = 3,25
Somit lauten die Koordinaten für den Schnittpunkt ( 0,25 | 3,25 )
Schritt 5: Gegenprobe
Um zu überprüfen, ob wir alles richtig gemacht haben, setzen wir den x-Wert auch in die Geradengleichung von g(x) ein.
G(x) = 0,25 + 3 = 3,25
Damit bekommen wir auch beim Einsetzen des x-Werts in die Funktion g (x) denselben Schnittpunkt heraus wie beim Einsetzen in f (x). Also haben wir alles richtig gemacht.
Aufgabe 2
Bestimme den Schnittpunkt folgender Geraden:
f(x) = 5*x + 6 (grün)
g(x) = 5*x + 1 (blau)
Lösung Aufgabe 2
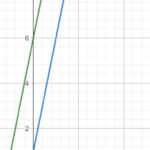
Schritt 1: Die Steigung der beiden Funktionen betrachten
Betrachten wir die Steigung der beiden Funktionen, sehen wir, dass beide dieselbe Steigung haben, da m=n und damit 5=5.
Trotzdem probieren wir es aus, den Schnittpunkt der Geraden zu bestimmen.
Schritt 2: Beide Gleichungen gleichsetzen
f(x) = g(x)
5*x + 1 = 5*x + 6
Schritt 3: Gleichungssystem auflösen
5*x + 1 = 5*x + 6 | -5*x
1 = 6
Das ist falsch! Da die beiden Geraden keinen Schnittpunkt besitzen, können wir auch keinen Schnittpunkt berechnen. So kannst du überprüfen, ob die Geraden wirklich parallel zueinander sind, falls du dir mal unsicher sein solltest.
FAQ zum Schnittpunkt zweier Geraden
Wie lautet die Funktionsgleichung einer Geraden?
Die allgemeine Funktionsgleichung lautet: f(x) = m*x + b
Dabei stellt m die Steigung der Geraden dar, und b den y-Achsenabschnitt.
Wie kann ich ablesen, ob sich zwei Geraden schneiden?
Zwei Geraden haben immer einen Schnittpunkt, wenn sie eine unterschiedliche Steigung haben. Dies kannst du an der Zahl vor dem x ablesen.
Wann schneiden sich zwei Geraden nicht?
Wenn zwei Geraden dieselbe Steigung haben, also die Zahl vor dem x bei beiden Geraden gleich ist, sind sie parallel zueinander.
Wenn sie einen unterschiedlichen y-Achsenabschnitt haben, haben sie keinen Schnittpunkt, bei einem gleichen y-Achsenabschnitt haben sie unendlich viele Schnittpunkte, da sie perfekt aufeinanderliegen.
Hat dir der Inhalt geholfen? Lass uns gerne einen kurzen Kommentar da, wir würden uns sehr freuen! Ansonsten findest du weitere hilfreiche Erklärungen zu verschiedenen Themengebieten auf der Homepage des Nachhilfe-Teams.
Du möchstest noch tiefer in die Mathe-Materie einsteigen? Dann komm ins Nachhilfe-Team. Egal ob Berlin, Köln oder München – unsere Mathe Hilfe ist in ganz Deutschland vertreten. Und auch Online kannst du bequem daran teilnehmen!
Unsere Ratgeber zum Kommutativgesetz, zur Monotonie und zu den binomischen Formeln hoch 3 könnten dich ebenfalls interessieren.

Pingback: Nullstellen berechnen - Einfach Schritt für Schritt erklärt
Gut erklärt, aber mehr Beispiele wären hilfreich.