3,50 von 5 Sterne
Loading...
Was ist denn noch mal ein Sattelpunkt? Und was ist der Unterschied zum Wendepunkt?
Stell dir vor, du fährst mit deinem Fahrrad einen Berg herunter. Zwischen drin gibt es ein kleines Stück, an dem du verschnaufen kannst und es nicht Bergab geht.
Diese Stück ist wie ein Sattelpunkt. Wie genau du den berechnest und vieles mehr, das zeigen wir dir jetzt!
Was ist ein Sattelpunkt?
Ein Sattelpunkt (auch Terrassenpunkt genannt) einer Funktion ist der Punkt eines Graphens, an dem die Steigung 0 ist und die Steigung vor diesem Punkt die Gleiche ist wie die Steigung danach (Graph fällt vorher und danach oder Graph steigt vorher und danach)
Der Sattelpunkt ist also eine spezielle Form eines Wendepunktes.
Wie erkenne ich einen Sattelpunkt?
Da er auch ein Wendepunkt ist, muss also die 2. Ableitung = 0 sein und die 3. Ableitung ungleich 0.
Zusätzlich kommt allerdings noch die Bedingung dazu, dass die 1. Ableitung auch = 0 sein muss, da dieser keine Steigung besitzt.
Er ist also ein Wendepunkt, ohne Steigung.
Beispiele und Unterschied zum Wendepunkt
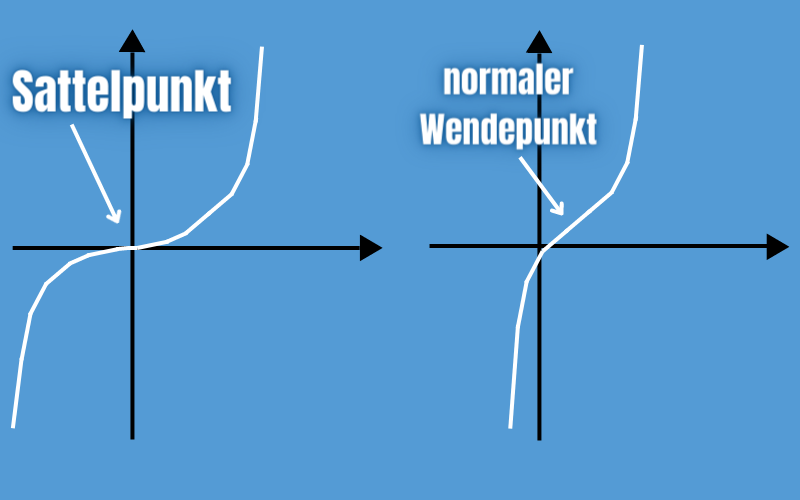
Der einzige Unterschied zu einem normalen Wendepunkt ist also die Steigung. Während sie bei einem Sattelpunkt immer null ist, gilt dies für einen normalen Wendepunkt nicht.
Hier zur Verdeutlichung 2 Graphen, einmal einen mit Sattelpunkt und einen mit normalen Wendepunkt.
Einen Sattelpunkt berechnen anhand der mathematischen Bedingungen
Schritt für Schritt berechnest du, ob es sich um einen Sattelpunkt handelt und wenn ja, wo genau sich dieser befindet.
Dabei nutzt du die mathematischen Bedingungen und Ableitungen.
Schritt 1: Ermittle die 1., 2. und 3. Ableitung einer Funktion.
Schritt 2: Berechne die Nullstellen der zweiten Ableitung der Funktion.
Schritt 3: Setze die Nullstellen der 2. Ableitung in die 3. Ableitung ein und überprüfe, ob diese ungleich 0 sind.
Schritt 4: Setze die Werte, die bei Schritt 3 ungleich 0 waren, in die 1. Ableitung ein. Wenn hier ebenfalls das Ergebnis 0 rauskommt, handelt es sich um einen Sattelpunkt. Wenn das Ergebnis ungleich 0 ist, ist es ein normaler Wendepunkt.
Schritt 5: Setze nun die X Werte der Sattelpunkte in die Funktion ein, um den Y-Wert zu berechnen.
Beispiel und Übungsaufgabe mit Rechenweg
Zur Überprüfung lass uns doch mal eine Beispielaufgabe berechnen.
Gegeben ist folgende Funktion f(x)= (x-1)^3 + 2
Überprüfe, ob die Funktion f(x) einen Sattelpunkt besitzt und wenn ja, gib die Koordinaten an, an denen er sich befindet.
Schritt 1: Ableitungen bilden
f´(x)= 3*(x-1)^2
f´´(x)= 6*(x-1)
f´´´(x)=6
Schritt 2: Berechnen der Nullstellen der 2. Ableitung
6*(x-1)=0
x-1=0
x = 1
->Bei x=1 ist die 2. Ableitung = 0
Schritt 3: Überprüfen ob dritte Ableitung bei x=1 ungleich 0 ist
f´´´(1)= 6
-> Die dritte Ableitung ist bei x=1 ungleich 0
Schritt 4: Überprüfen ob es ein Sattelpunkt ist
f´(1) = 3*(1-1)^2 = 3*0^2 = 0
-> Es handelt sich um einen Sattelpunkt
Schritt 5: Y-Koordinate bestimmen
f(1) = (1-1)^3 +2 = 0 + 2 = 2
Der Sattelpunkt befindet sich bei P(1 / 2)
So einfach kannst du also vorgehen, um die Sattelpunkte zu bestimmen, wenn es denn welche gibt. Schau doch ebenfalls bei unserem Artikel zur Analysis rein.
Wir hoffen wir konnten dir die Sattelpunkte gut erklären. Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung und einen Kommentar hinterlässt. Vielen Dank!
3,50 von 5 Sterne
Loading...
