4,20 von 5 Sterne
Loading...
Der Mittelwert ist ein mathematisches Konzept, dem du im Alltag bestimmt häufiger begegnest. Oftmals auch mit dem Namen “Durchschnitt”. Doch was genau steckt dahinter und wie berechnet man diesen?
Hier erfährst du alles was du über den Mittelwert bzw. den Durchschnitt wissen musst!
Wir liefern dir…
…einfache Erklärungen
…anschauliche Beispiele und
…Übungsaufgaben zum Selbsttest
Lass uns loslegen!
Mittelwert Definition
Der Mittelwert (auch arithmetisches Mittel oder Durchschnitt) ist die
Summe aller Zahlen geteilt durch die Anzahl der Zahlen.
Er eignet sich, um z.B. den Durchschnitt von Preisen, Temperaturen oder Schulnoten zu berechnen. Das mathematische Symbol ist ein x mit einem geraden Strich darüber: X̅
Mittelwert berechnen
Als Beispiel sind folgende Zahlen gegeben:
4 3 7 5 1
Um den Mittelwert zu berechnen, wird erst die Summe dieser Zahlen berechnet:
4 + 3 + 7 + 5 + 1 = 20
Nun wird die Summe durch die Anzahl der Zahlen geteilt. Diese ist 5:
20/5 = 4
Mittelwert Formel:
Übungsaufgaben Mittelwert
Berechne den Mittelwert folgender Zahlen:
a) 6, 8, 7
b) 2, 5, 6, 3
c) 3, 7, 5, 9, 1
a) 7
b) 4
c) 5
Mittelwert Diagramme
Im Unterricht oder in Mathe-Tests werden häufig Aufgaben gestellt, indem der Mittelwert aus Diagrammen berechnet oder diese in die Diagramme gezeichnet werden sollen. Dies geht leichter als du denkst!
Angenommen, du sollst den Notendurchschnitt für die letzte Mathearbeit aus einem Schulnoten-Diagramm entnehmen. Das Diagramm sieht so aus:
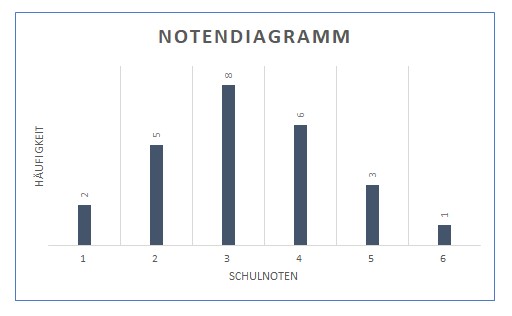
Möchtest du nun den Mittelwert berechnen, musst du wie folgt vorgehen:
- Du multipliziert jede Schulnote mit deren Häufigkeit
- Du addierst die Ergebnisse zusammen
- Zum Schluss teilst du die Summe durch die Gesamthäufigkeit
Wenn du die Schulnote mit deren Häufigkeit multiplizierst, erhältst du diese Rechnungen:
1 • 2 = 2
2 • 5 = 10
3 • 8 = 24
4 • 6 = 24
5 • 3 = 15
6 • 1 = 6
Die Summe der Ergebnisse lautet:
2 + 10 + 24 + 24 + 15 + 6 = 81
Nun teilst du die Summe durch die Gesamthäufigkeit (Anzahl an Noten). Diese ist 25:
81/25 = 3,24
Die durchschnittliche Schulnote ist also 3,24.
Übungsaufgaben – Diagramme
Die Klasse 7b hat sich vor Weihnachten gegenseitig mit Geschenken beschenkt. Dabei wurden unterschiedliche Preise für die Geschenke bezahlt. Du hast nun die Aufgabe den Durchschnittspreis aller Geschenke der Klasse zu berechnen. Dafür hast du eine Befragung durchgeführt und folgende Tabelle erhalten:
Preis 10€ 8€ 6€ 4€ 2€ Häufigkeit 2 3 6 11 8
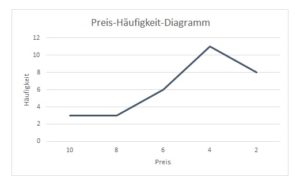
a) Zeichne das Preis-Häufigkeit-Diagramm
b) Berechne den Durchschnittspreis der Klasse
a)
Hinweis: Ein Balkendiagramm ist ebenfalls richtig!
b)
\frac{10*2 + 8*3 + 6*6 + 4*11 + 2*8}{30}
= \frac{140}{30}
= 4 \frac{2}{3} oder 4,67
Häufig gestellte Fragen / FAQ
Der Mittelwert ist die Summe der gegebenen Zahlen geteilt durch die Anzahl der gegebenen Zahlen.
Man kann ihn zum Berechnen von Durchschnittspreisen, Durchschnittstemperaturen, Notendurchschnitte oder alle anderen Mittelwerte für den Alltag oder für die Statistik verwenden.
Der Mittelwert wird auch als Durchschnitt bzw. Durchschnittswert bezeichnet.
Man berechnet die Summe der Zahlen und teilt diese durch die Anzahl der Zahlen
Na, weißt du nun alles, was du über den Mittelwert wissen wolltest?
Interesse an weiteren Themen aus der Mathematik? Willst du wissen, wie man Wahrscheinlichkeiten berechnet oder suchst du Erklärungen und Aufgaben zum Thema Dreisatz? Dann schaue gern bei unseren Artikeln vorbei oder komme für eine Probestunde in unsere Mathe Nachhilfe! Wir sind sogar Online stets flexibel für dich da.
Hat dir der Artikel gefallen und konnten wir dir weiterhelfen? Lasse uns dein Feedback oder noch offene Fragen sehr gerne in den Kommentaren da, wir freuen uns! ?