Vektorrechnung: Addition, Subtraktion, Multiplikation schnell erklärt

(Noch keine Bewertungen)

Vektoren sind ein sehr ausführliches Thema. Du weißt bereits was Vektoren sind? Du verstehst nur noch nicht so ganz wie du mit ihnen rechnest? Dann bist du hier genau richtig! In diesem Artikel schauen wir uns gemeinsam die grundlegende Vektorrechnung an. Von der Addition und Subtraktion von Vektoren bis hin zur Multiplikation besprechen wir alles Step-by-Step. Außerdem klären wir, ob man Vektoren auch dividieren kann.

Inhalt

Vektoren addieren

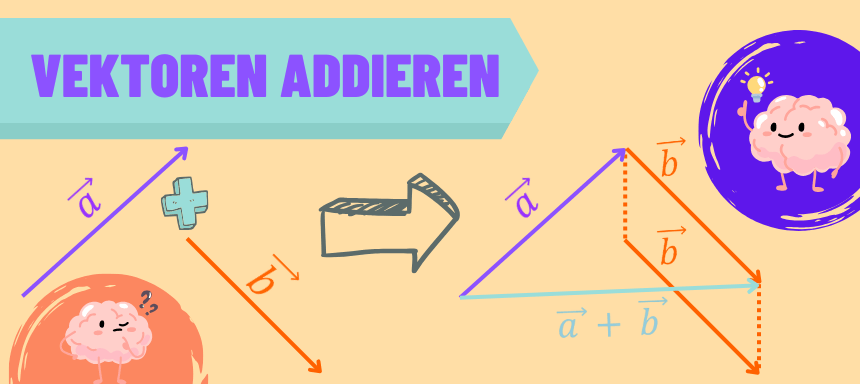
Um zwei oder mehrere Vektoren miteinander addieren zu können, musst du jeweils die einzelnen Komponenten zusammenrechnen.

In der Ebene
Im Raum

In der Ebene

Für die Addition von zwei Vektoren in der Ebene $\vec{a} = \left[\begin{array}{cc} a_1 \\ a_2 \end{array}\right]$ und $\vec{b} = \left[\begin{array}{cc} b_1 \\ b_2 \end{array}\right]$ gilt also:

$\vec{a} + \vec{b} = \left[\begin{array}{ccc} a_1 & + & b_1 \\ a_2 & + & b_2 \end{array}\right]$

Beispiel:

$\vec{a}=\left[\begin{array}{cc} 3\\ 6 \end{array}\right]$ und $\vec{b}=\left[\begin{array}{cc} -2 \\ 4\end{array}\right]$

$\vec{a} + \vec{b} = \left[\begin{array}{ccc} 3 & + & -2\\ 6 & + & 4 \end{array}\right] = \left[\begin{array}{cc} 1\\ 10 \end{array}\right]$

Im Raum

Analog gilt für die Addition von zwei Vektoren im Raum $\vec{f}=\left[\begin{array}{ccc} f_1 \\ f_2\\ f_3\end{array}\right]$ und $\vec{g}= \left[\begin{array}{ccc} g_1 \\ g_2\\ g_3\end{array}\right]$

$\vec{f} + \vec{g} = \left[\begin{array}{ccc} f_1 & + & g_1 \\ f_2 & + & g_2 \\ f_3 & + & g_3 \end{array}\right]$

Beispiel:

$\vec{f}=\left[\begin{array}{ccc} 3\\ -4\\ -4\end{array}\right]$ und $\vec{g}= \left[\begin{array}{ccc} 2 \\ 6\\ 1\end{array}\right]$

$\vec{f} + \vec{g} = \left[\begin{array}{ccc} 3 & + & 2 \\ -4 & + & 6 \\ -4 & + & 1 \end{array}\right] = \left[\begin{array}{ccc} 5 \\ -2 \\ -3 \end{array}\right]$

Merke dir: Bei der Addition von Vektoren erhält man einen Repräsentanten eines sogenannten Summenvektors. Er wird zum Beispiel als $\vec{a} + \vec{b}$ bezeichnet.

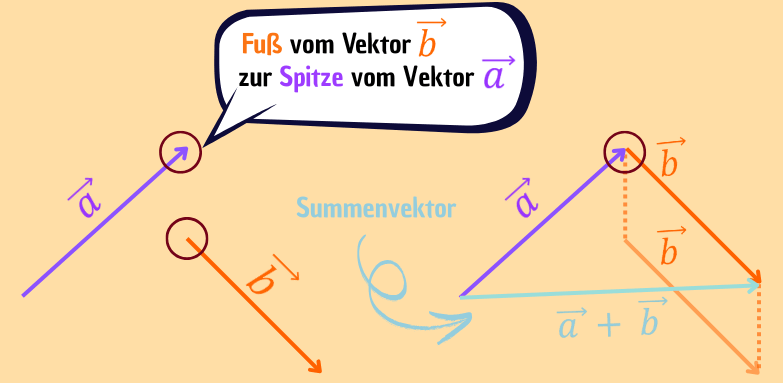
Auch grafisch kann man die Addition von Vektoren veranschaulichen. Hierfür fügst du geeignete Repräsentanten von $\vec{a}$ und $\vec{b}$ aneinander. Der Summenvektor $\vec{a} + \vec{b}$ geht dann vom Ausgangspunkt (Fuß) des Vektors $\vec{a}$ zur Spitze des angefügten Repräsentanten von $\vec{b}$ .

Für die Vektoraddition gelten die gleichen Rechengesetze wie für die Addition von Zahlen:

Kommutativgesetz der Addition

$\vec{a} + \vec{b} = \vec{b} + \vec{a}$

Assoziativgesetz

$\vec{a} + \vec{b} + \vec{c} = (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$

Vektoren subtrahieren

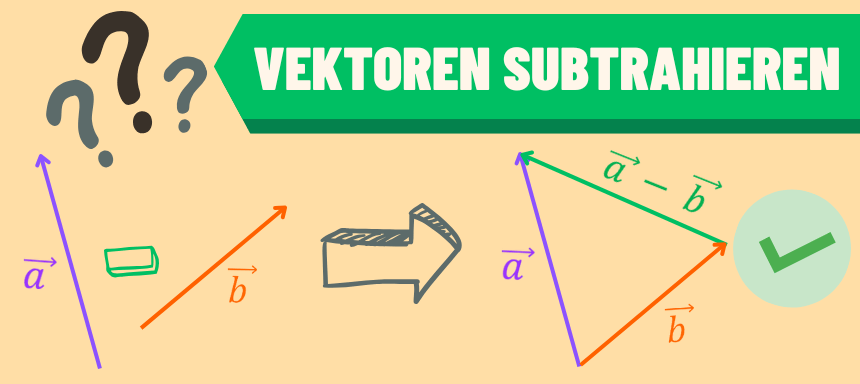
Ein weiterer Bestandteil der Vektorrechnung ist die Subtraktion von Vektoren. Mathematisch betrachtet ist die Differenz zwischen einem Vektor $\vec{a}$ und einem Vektor $\vec{b}$ definiert als die Summe aus dem Vektor $\vec{a}$ und dem Gegenvektor von $\vec{b}$ .

Es gilt:

$\vec{a} - \vec{b} = \vec{a} + (\vec{-b})$

Beispiel:

$\vec{a} = \left[\begin{array}{ccc}2\\6\end{array}\right]$ und $\vec{b} = \left[\begin{array}{ccc}5\\3\end{array}\right]$

$\vec{a} - \vec{b} = \left[\begin{array}{ccc}2 & - & 5\\6 & - & 3\end{array}\right] = \left[\begin{array}{ccc} -3\\ 3\end{array}\right]$

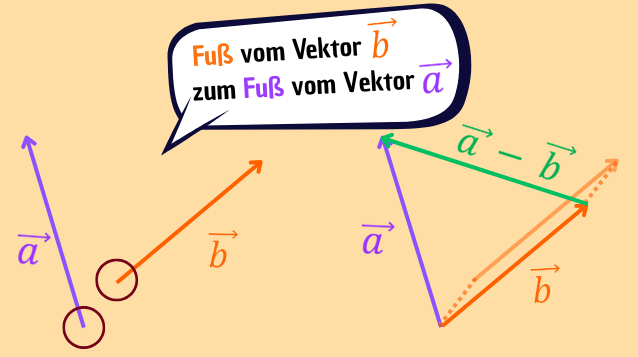
Auch die Subtraktion von Vektoren kann grafisch veranschaulicht werden: Einen Repräsentanten von $\vec{a} - \vec{b}$ erhältst du, indem du von der Spitze eines Repräsentanten des Vektors $\vec{b}$ zur Spitze eines Repräsentanten des Vektors $\vec{a}$ gehst.

Vektoren subtrahieren grafische Darstellung

Vektoren multiplizieren

Bei der Multiplikation von Vektoren gibt es insgesamt drei verschiedene Verfahren.

Multiplikation von Vektoren drei Verfahren Übersicht

Jede dieser Berechnungen hat einen eigenen Zweck. Welche Berechnung du für was anwendest zeigt dir diese Tabelle.

	Was wird multipliziert?	Was erhält man als Ergebnis?	Was ist der Zweck der Berechnung?
Skalarmultiplikation	Vektor und Zahl	Vektor	Strecken/ Stauchen eines Vektors
Skalarprodukt	Zwei Vektoren	Zahl	Nachweis eines rechten Winkels zwischen zwei Vektoren
Kreuzprodukt	Zwei Vektoren	Vektor, der senkrecht auf den anderen zwei Vektoren steht	Ermitteln eines Normalenvektors; Flächenberechnung

Achtung!

Im strengen mathematischen Sinne, ist nur die Skalarmultiplikation eine Multiplikation. Denn nur hier wird mit einer Zahl multipliziert. Das Skalar- und Kreuzprodukt sind lediglich mathematische Vorgehensweisen, die aber an eine Multiplikation erinnern.

1.

Skalarmultiplikation (Vektor mit Zahl multiplizieren)

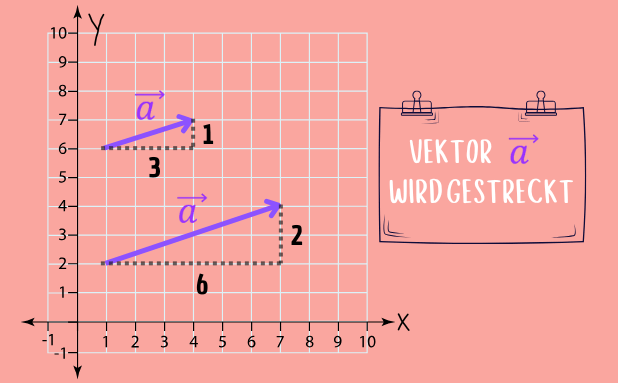
Hierbei multiplizierst du einen Vektor mit einer Zahl. Diese Zahl wird Skalar genannt. Durch die Skalarmultiplikation kannst du deinen Vektor strecken und stauchen. Außerdem kann seine Richtung geändert werden.

Berechnung:

Du multiplizierst den Skalar k mit jeder Komponente deines Vektors $\vec{a}$ .

$k \cdot \vec{a} = k \cdot \left[\begin{array}{cc} a_1 \\ a_2 \end{array}\right] = \left[\begin{array}{ccc} k & \cdot & a_1 \\ k & \cdot & a_2 \end{array}\right]$

Beispiel:

Wenn du einen Vektor $\vec{a} = \left[begin{array}{cc} 3 \\ 1 \end{array}\right]$ mit dem Skalar k = 2 multiplizierst, dann erhältst du folgenden Vektor:

$2 \cdot \vec{a} = 2 \cdot \left[\begin{array}{ccc} 3\\ 1 \end{array}\right] = \left[\begin{array}{ccc} 2 & \cdot & 3\\ 2 & \cdot & 1 \end{array}\right] = \left[\begin{array}{ccc} 6\\ 2 \end{array}\right]$

Skalarmultiplikation grafische Darstellung

Merke dir!

Ist der Skalar größer als 1 ⇒ wird der Vektor gestreckt.
Ist der Skalar zwischen 0 und 1 ⇒ wird der Vektor gestaucht.
Hat der Skalar ein negatives Vorzeichen ⇒ wird die Richtung des Vektors geändert.

2.

Skalarprodukt – inneres Produkt von Vektoren

Das Skalarprodukt verwendest du, um eine reelle Zahl, das sogenannte Skalar zu bestimmen. Außerdem kannst du mithilfe des Skalarprodukts den Winkel zwischen zwei Vektoren berechnen. Zudem kannst du prüfen, ob sie orthogonal zueinander sind, also senkrecht aufeinander stehen. Du kannst nur Vektoren aus denselben Dimensionen miteinander multiplizieren.

Das heißt:

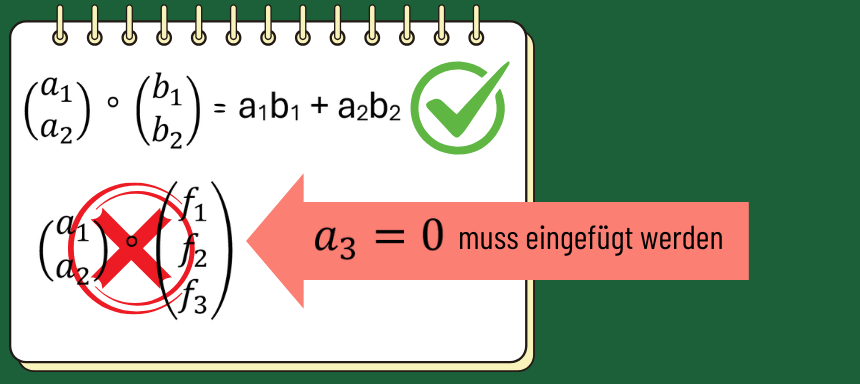
Skalarmultiplikation nur dieselben Dimensionen

3.

Kreuzprodukt (Vektorprodukt) – äußeres Produkt von Vektoren

Das Kreuzprodukt dient dazu einen Vektor zu berechnen, der senkrecht auf den zwei bereits gegebenen Vektoren steht. Dies kannst du nur bei Vektoren im Raum berechnen. Eine häufige Anwendung ist die Berechnung von Flächeninhalten und Volumina (Spatprodukt).

$\left[\begin{array}{ccc} a_1 \\ a_2 \\ a_3 \end{array}\right] \times \left[\begin{array}{ccc} b_1 \\ b_2 \\ b_3 \end{array}\right] = \left[\begin{array}{ccc} a_2b_3 & - & a_3b_2\\ a_3b_1 & - & a_1b_3 \\ a_1b_2 & - & a_2b_1 \end{array}\right]$

Vektoren dividieren

Die wichtigsten Bestandteile der Vektorrechnung, nämlich die Addition, Subtraktion und Multiplikation von Vektoren haben wir durchgearbeitet, super! Nun klären wir noch, ob die Division ebenfalls Teil der Vektorrechnung ist.

Grundsätzlich ist die Division die Umkehroperation der Multiplikation. Allerdings haben wir gerade besprochen, dass in der linearen Algebra die Multiplikation für Vektoren nicht eindeutig definiert ist. Somit ist auch die Division von Vektoren nicht definiert.

Dennoch gibt es mathematische Vorgehensweisen, die der uns bekannten Division bei Zahlen ähnelt. Diese schauen wir uns nun genauer an.

Division eines Vektors durch einen Skalar
Division eines Vektors durch seinen Betrag

1.

Division eines Vektors durch einen Skalar

Dieses Vorgehen funktioniert ähnlich wie die Skalarmultiplikation. Analog zur Skalarmultiplikation können durch diese mathematische Operation Vektoren gestaucht und ihre Richtung verändert werden.

Berechnung:

Du dividierst jede Komponente deines Vektors $\vec{a}$ durch den Skalar k.

Beispiel:

Wenn du einen Vektor $\vec{a} = \left[\begin{array}{ccc} 3\\ 6 \end{array}\right]$ durch den Skalar k = 3 dividierst, dann erhältst du folgenden Vektor:

$\vec{a} : 3 = \left[\begin{array}{ccc} 3\\ 6 \end{array}\right] : 3 = \left[\begin{array}{ccc} 3 & : & 3\\ 6 & : & 3\end{array}\right] = \left[\begin{array}{ccc}1\\ 2 \end{array}\right]$

Tipp!

Bei gewissen Berechnungen kann es hilfreich sein mit dem Kehrbruch des Skalars zu multiplizieren, anstatt durch das Skalar zu dividieren. Man erhält das gleiche Ergebnis!

Beispiel:

$\vec{a} : 3 = \left[\begin{array}{ccc} 3\\ 6 \end{array}\right] \cdot \frac{1}{3} = \left[\begin{array}{ccc} 3 & \cdot & \frac{1}{3} \\ 6 & \cdot & \frac{1}{3} \end{array}\right] = \left[\begin{array}{ccc} \frac{3}{3} \\ \frac{6}{3} \end{array}\right] = \left[\begin{array}{ccc} 1 \\ 2 \end{array}\right]$

2.

Division eines Vektors durch seinen Betrag

Wenn du einen Vektor durch seinen Betrag teilst, dann erhältst du als Ergebnis einen Einheitsvektor, der in dieselbe Richtung wie der Ausgangsvektor zeigt. Dieser Einheitsvektor hat die Länge 1.

Mehr zur Berechnung eines Einheitsvektors und den Basisvektoren erfährst du in unserem Einführungsartikel zu Vektoren.

Wir haben uns sehr bemüht, dir das Thema Vektorrechnung anschaulich näher zu bringen. Wir hoffen du blickst jetzt durch! Wir würden uns riesig freuen, wenn du uns eine Sternebewertung hinterlässt. Vielen Dank! 🙂
(Noch keine Bewertungen)
Loading...

Vektoren addieren

In der Ebene

Im Raum

Kommutativgesetz der Addition

Assoziativgesetz

Vektoren subtrahieren

Vektoren multiplizieren

1.

Skalarmultiplikation (Vektor mit Zahl multiplizieren)

2.

Skalarprodukt – inneres Produkt von Vektoren

3.

Kreuzprodukt (Vektorprodukt) – äußeres Produkt von Vektoren

Vektoren dividieren

1.

Division eines Vektors durch einen Skalar

2.

Division eines Vektors durch seinen Betrag

Kommentar verfassen Kommentieren abbrechen