5,00 von 5 Sterne
Loading...
Du möchtest alles über Pyramiden wissen? Wissen, wie man das Volumen und die Oberfläche berechnen kann und außerdem die besonderen Arten von Pyramiden kennenlernen? Dann bist du hier richtig.
Lass mich dir die Welt der Pyramiden Schritt für Schritt näherbringen.
Los geht’s!
Die Pyramide ist eine der vielen geometrischen Körper in der Geometrie. Die Pyramide hat als Grundfläche ein Vieleck und die Mantelfläche besteht aus mindestens 3 gleichschenkligen Dreiecken. Die Mantelfläche einer Pyramide hat genauso viele Dreiecke wie die Grundfläche Seiten hat.
Die gängigste und bekannteste Pyramide ist die quadratische Pyramide. Sie hat als Grundfläche ein Quadrat und somit vier gleichschenklige Dreiecke als Mantelfläche.
Netz
Als Netz einer Pyramide bezeichnet man alle Seite der Pyramide auf einer Ebene ausgebreitet. Dabei können die einzelnen Flächen unterschiedlich aneinander gereiht werden. Wichtig ist, dass sich eine Pyramide bildet, wenn man das Netz an den Kanten faltet.
Es gibt weitere Arten von Pyramiden, die alle unterschiedliche Grundflächen haben und somit auch verschiede Anzahlen an Dreiecken in der Mantelfläche besitzen. Aber dazu später mehr.
Pyramide berechnen
Kommen wir zum spannenden Teil des Artikels und somit auch zu dem Teil, in dem du lernen kannst, wie du Schritt für Schritt Pyramiden berechnen kannst.
Berechnen wir als Erstes das Volumen.
Die allgemeine Formel zur Volumenberechnung lautet:
V = 1/3 * G *h
G die Grundfläche und h die Höhe
Kommen wir zur Oberfläche – die allgemeine Formel lautet:
O = G + M
G ist die Grundfläche und M die Mantelfläche
Du fragst dich was hinter G und M steckt? Dies hängt von der Grundfläche der Pyramide ab, da sie verschiedene Formen annehmen kann. Somit ist die Mantelfläche ebenfalls abhängig. Das heißt, je nachdem wie viele Seiten die Grundfläche hat, hat die Mantelfläche Dreiecke als Seitenfläche.
Ich zeige dir zwei Beispiele, mit denen ich dir das Berechnen von Pyramiden näher bringen werde.
Quadratischen Pyramide
Volumen
Der erste Schritt ist es, sich immer Gedanken über die Grundfläche zu machen. Diese Pyramide hat als Grundfläche ein Quadrat. Die Flächenformel für das Quadrat ist Seite multipliziert mit der Seite. In dem Fall sind die Seiten gleich lang.
A = a * a = a²
Um also das Volumen einer quadratischen Pyramide zu berechnen, muss man das G, durch a² ersetzen. Somit lautet die Formel:
V = 1/3 * a² * h
Oberfläche
Um die Oberfläche zu berechnen, brauchst du G und M. G haben wir schon ausgerechnet (G = 25cm²) also bleibt noch M. Für die Mantelfläche brauchst du den Flächeninhalt eines Dreieckes.
Dieser lautet:
A = ½ * ha * a
ha ist die Höhe des Dreiecks
Um die gesamte Mantelfläche berechnen zu können, muss diese Dreiecksflächen mit 4 multipliziert werden, da die quadratische 4 solcher Dreiecksflächen hat.
Jetzt gibst du die Werte in die Oberflächenformel ein.
Rechteckige Pyramide
Das zweite Beispiel ist eine rechteckige Pyramide.
Volumen
Auch hier ist dein erster Schritt wieder die Grundfläche. Diese Pyramide hat ein Rechteck als Grundfläche. Die Flächenformel für ein Rechteck lautet:
A = a * b
Also wird G durch a * b in der Volumenformel ersetzt. Dies sieht dann wie folgt aus:
V = 1/3 * a * b * h
Oberfläche
Die Grundfläche haben wir schon oben berechnet. Die Mantelfläche besteht auch hier aus vier Dreiecken. Wie bei einem Rechteck, sind auch hier die gegenüberliegenden Seiten gleich groß. Die Flächenformeln lauten dementsprechend:
Aa = ½ * a * ha
Ab = ½ * b * hb
ha ist die Höhe des Dreiecks auf der Seite a
hb ist die Höhe des Dreiecks auf der Seite b
Uns ist weder Seitenhöhe ha noch Seitenhöhe hb bekannt. Diese können wir durch die Anwendung des Satz des Pythagoras bestimmen, denn dieser stellt eine Beziehung zwischen der drei Seitenlängen eines rechtwinkligen Dreiecks her.
Dabei ist die eine Kathete die Höhe der Pyramide h und die zweite Kathete ist jeweils die Hälfte der Seiten a oder b. Die Hypotenuse ist somit ha bzw. hb.
Rechnerisch sieht dies so aus:
Für Seite b – nach hb umstellen:
a/2² + h² = hb² –> hb=√(a/2² + h² )
Für Seite a – nach ha umstellen:
b/2² + h² = ha² –> ha=√( b/2² + h²)
Jetzt können wir endlich den Dreiecksflächeninhalt bestimmen.
Die Mantelfläche besteht aus zwei mal den Flächeninhalten der Seiten a und b.
Die Oberfläche ist nun leicht zu bestimmen.
Besondere Arten von Pyramiden
Bezeichnung | Skizze | Formel |
Dreiecks Pyramide |  | Volumen:
|
Quadratische Pyramide |  | Volumen:
|
Rechteckige Pyramide |  | Volumen:
Pythagoras hb² = a/2² + h² ha² = b/2² + h² M = 2 * Aa + 2 * Ab |
Sechseckige Pyramide |  | Volumen:
M = a * ha * 3 |
Hier findest du die Tabelle zum Downloaden: Besondere Arten von Pyramiden
Pyramiden Übungen
Damit du dein Wissen vertiefen und anwenden kannst, findest du hier einige Aufgaben zum lösen.
Gib die Grund-, die Mantel- und die Oberfläche der quadratischen Pyramide an.
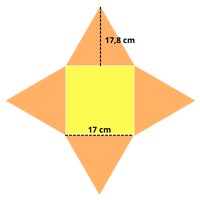
Grundfläche: 289 cm
Mantelfläche: 605,2 cm
Oberfläche: 894,2 cm
Berechne die fehlenden Werte der quadratischen Pyramiden.
a)
G = 87cm²
M = 100cm²
O = ?
b)
G = 57cm²
M = ?
O =193cm²
c)
a = 15cm
h Dreieck = 36cm
O = ?
d)
a = 13cm
h Dreieck = ?
0 = 793cm²
a)
G = 87cm²
M = 100cm²
O = 187cm²
b)
G = 57cm²
M = 136cm²
O = 193cm²
c)
a = 15cm
h Dreieck = 36cm
O = 1305cm²
d)
a = 13cm
h Dreieck = 26cm
O = 793cm²
Das Volumen einer quadratischen Pyramide beträgt 5.355cm³. Eine Seite der Grundfläche ist 42cm lang. Wie hoch ist die Pyramide?
Die Pyramide ist 255cm hoch.
Berechne alle Werte der folgenden Pyramide.
Pyramide | 1 | 2 | 3 | 4 |
Grundkante a | 7,5cm | 28dm | 19,5m | ? |
Grundkante b | 12cm | 10,2dm | ? | 26,1m |
Pyramidenhöhe h | 8cm | ? | 7m | 6m |
Volumen | ? | 1428dm³ | 364m³ | 1305m³ |
Pyramide | 1 | 2 | 3 | 4 |
Grundkante a | 7,5cm | 28dm | 19,5m | 25m |
Grundkante b | 12cm | 10,2dm | 8m | 26,1m |
Pyramidenhöhe h | 8cm | 5dm | 7m | 6m |
Volumen | 240cm³ | 1425dm³ | 364m³ | 1305m³ |
Pyramiden berechnen – FAQ
Was ist eine Pyramide?
Eine Pyramide besteht aus Grundfläche und Mantelfläche. Dabei besteht die Mantelfläche aus Dreiecken.
Was ist ein Netz einer Pyramide?
Als Netz einer Pyramide bezeichnet man alle Seite der Pyramide auf einer Ebene ausgebreitet.
Wie lautet die allgemeine Volumen Formel einer Pyramide?
V = 1/3 * G * h
Wie lautet die allgemeine Oberflächenformel einer Pyramide?
O = M * G
Konnte dieser Artikel dir die Welt der Pyramiden näher bringen? Lass uns doch eine Sternebewertung und deinen Kommentar dazu da. Auch über konstruktives Feedback freuen wir uns sehr. Vielen Dank! 5,00 von 5 Sterne
Loading...
Diese Artikel könnten auch interessant für dich sein: