Mengen leicht erklärt: Definitionen und Beispiele

Im Matheunterricht beginnt ihr mit Wahrscheinlichkeiten und Vereinigungsmenge, Schnittmenge, Differenzmenge… sagen dir nichts?

Kein Problem- das bekommen wir in den Griff, denn die Mengenlehre ist viel leichter, als du denkst!

In diesem Beitrag wirst du… :

• verstehen, was Mengen und Elemente sind.
• die Grundlagen der Mengenlehre mit Hilfe von Mengendiagrammen lernen.
• dein Wissen mit Beispielaufgaben vertiefen.

Legen wir los und schauen uns gemeinsam Schritt für Schritt an, was hinter der Mengenlehre steckt.

Mengen und Elemente

Mengen und Elemente werden wie folgt definiert:

Diese Definition besagt, dass Elemente die einzelnen Bestandteile einer Menge sind. Also ist eine Menge die Gesamtheit ihrer Elemente. Hier sind einige Beispiele für Mengen:

• Bäume in einem Park
• Filme, die zurzeit im Kino laufen
• Schulfächer deiner Schule
• Bücher in der Bücherei

Mengenlehre- mit Mengendiagramm

Bei der Mengenlehre gibt es einige Dinge, die zu beachten sind:

• Elemente der Menge werden in einer geschweiften Klammer aufgelistet. Dort kommen die Elemente jeweils nur einmal vor. Zum Beispiel:

Z = {a, b, c}       ⇒ Z ist eine Menge. Die Elemente von Z sind a, b und c.

Es gibt aber auch andere Schreibweisen. Eine davon wäre:

a, b, c    ∈    Z     ⇒ a, b und c sind Elemente der Menge Z.

(Wenn dies nicht so wäre, dann: a, b, c    ∉     Z )

• Wenn man jede Menge zusammenzählt, ergibt das die Grundgesamtheit Ω. Sagen wir: Alle Klassen in deiner Schule ergeben die Grundgesamtheit.

Schauen wir uns nun die Mengenlehre genauer an.

Schnittmenge/ Durchschnittsmenge

Die Schnittmenge wird manchmal auch die Durchschnittsmenge genannt, das ist, wenn sich Elemente von verschiedenen Mengen schneiden.

Stell dir vor: Du gehst in den Religionsunterricht oder in deinen Französischunterricht und dort sind auch andere Schüler aus anderen Klassen. Ihr beide gehört zu verschiedenen Klassen, aber seid in diesem Unterricht zusammen. Die jeweilige Schnittmenge wäre dieser Unterricht dann.

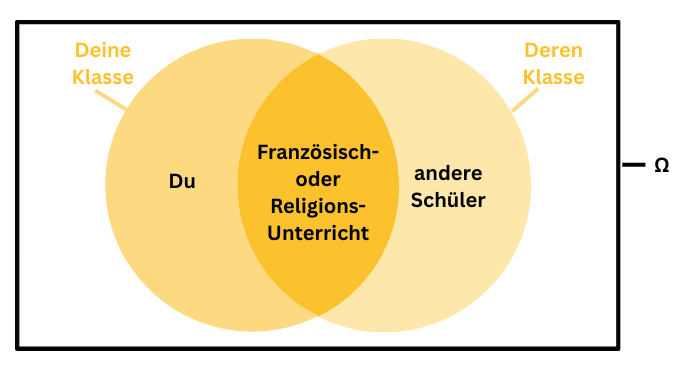
(Das ist ein Mengendiagramm, auch Venn-Diagramm genannt. Es wird zur Veranschaulichung von Mengen benutzt.) 

disjunkter Fall

Ein disjunkter Fall ist, wenn Mengen keine Schnittmenge haben. Die Mengenschreibweise ist dann:

A ∩ B = Ø   ⇒ A und B sind disjunkt.

Vereinigungsmenge

Bei der Vereinigungsmenge kommen alle Elemente der jeweiligen Menge vor. Man fasst also die Mengen zusammen. Hier ein Beispiel dafür:

Vorher:
A = {1, 2, 3}
B = {3, 4, 5}

Differenzmenge

Unter Differenzmenge versteht man die Elemente einer Menge, die nicht in einer anderen Menge enthalten sind. In der Mengenschreibweise wird das in folgender Art geschrieben: A \ B = {1, 2}

Nachher:
A ∪ B = {1, 2, 3, 4, 5}

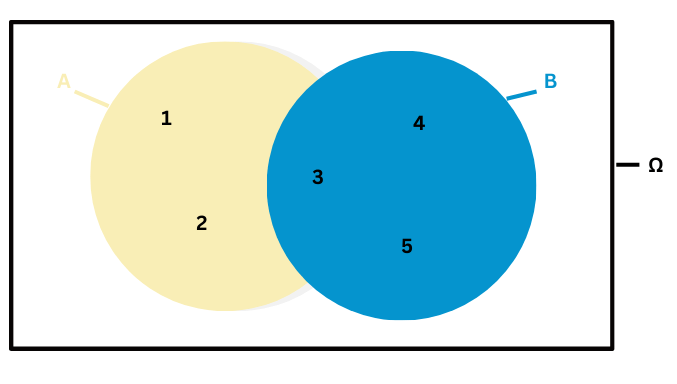
Also Elemente von A, die auch in B sind, werden nicht beachtet. Hier ist es die Zahl 3, daher bleiben nur die Zahlen 1 und 2 über.

Achtung: Nur die Elemente von A, die übrigbleiben, sind hier gewollt! Wenn es B \ A wäre, wären es die Elemente von B, die übrig bleiben, also 4 und 5.

Teilmenge und Obermenge

Wenn alle Elemente der Menge A auch in der Menge B vorhanden sind, ist die Menge A die Teilmenge von B. B ist dann die Obermenge.

Beispielsweise:
A = {1, 2, 3}
A ⊂ B = {1, 2, 3, 4, 5}

A ⊂ B = {1, 2, 3, 4, 5}

Falls B die gleichen Elemente wie A hat, dann schreibt man Folgendes:
A ⊆ B = {1, 2, 3}

A ⊆ B = {1, 2, 3}

Wenn du jetzt noch mehr über Teilmengen und über verschiedene Gesetze lernen willst, findest du hier eine gute Übersicht: Serlo – Mengenlehre

Mengenvergleich- Mächtigkeit/ Kardinalität

Die Elemente einer Menge entsprechen der Mächtigkeit (auch Kardinalität).

Beispiel:

• A = {45, 101, 88, 67}
• B = {1, 2}
• C = { }

⇒ Mächtigkeit: |A| = 4
⇒ Mächtigkeit: |B| = 2
⇒ Mächtigkeit: |C| = 0

Es gibt 2 Fälle bei dem Mengenvergleich.

• Gleichmächtigkeit: Die beiden Mengen haben die gleiche Mächtigkeit. Zum Beispiel: |A| = 3, |B| = 3, |A| = |B|
• Mächtiger als die andere Menge: Eine der beiden Mengen ist mächtiger bzw. hat mehr Elemente als die andere Menge. Beispielsweise:

|A| = 1, |B| = 4, |B| > |A| oder |A| < |B|

Komplement

Das Komplement oder auch Komplementärmenge genannt ist alles, was das “Gegenteil” der jeweiligen Menge ist, dazu gehören auch Schnittmengen.

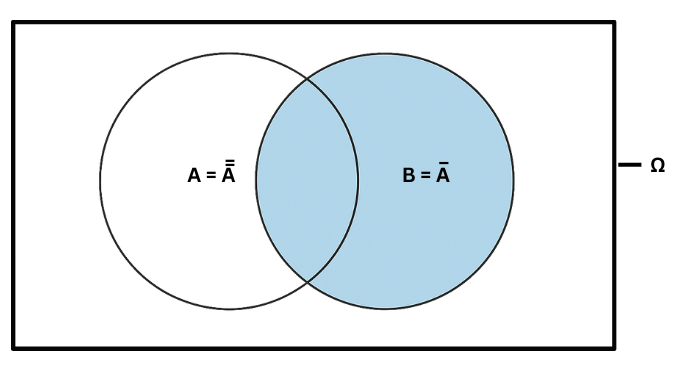
Das heißt, alles in der Grundgesamtheit außer A ist das Gegenteil/ Komplement von A. Daher wird das Komplement auch mit einem Strich über dem Buchstaben gekennzeichnet. Wenn es einen Doppelstrich gibt, ist es die Ausgangsmenge wieder.

Fall: leere Menge

Falls es in einer Menge keine Elemente gibt, wird dies als leere Menge bezeichnet. Die Mengenschreibweise dafür lautet: { } oder: Ø

Das war’s auch schon mit dem Artikel zur Mengenlehre. Ich hoffe, du konntest etwas mitnehmen und hast jetzt einen besseren Überblick über die Grundbegriffe.