(Noch keine Bewertungen)
Loading...
Definitionsbereiche bereiten dir Schwierigkeiten? Keine Sorge, das wird sich nach diesem Artikel ändern.
Denn hier wirst du… :
- den Unterschied zwischen Definitions- und Wertebereichen verstehen.
- Definitionsbereiche verschiedenster Funktionen berechnen können.
- dein Wissen mit einem Quiz testen können.
Bist du bereit? Auf die Plätze, fertig, los!
mathematischer Fehler:
Ein mathematischer Fehler entsteht beispielsweise, wenn man durch Null teilt oder die Wurzel von einer negativen Zahl zieht.
Wertebereich:
Alle y-Werte, die als Ergebnis der Funktion herauskommen können, wenn man die x-Werte vom Definitionsbereich einsetzt.
Definitionsbereiche bestimmen und berechnen- mit Beispielaufgaben
Wie man die Definitionsbereiche bestimmt, ändert sich mit jedem Funktionstyp. Bevor wir uns die verschiedenen Funktionen anschauen, solltest du die Zahlenmengen kennen.
lineare und quadratische Funktionen
Bei einer linearen und quadratischen Funktion ist es so, dass man alle Zahlen für den Definitionsbereich nutzen kann. Der Grund dafür ist, dass die beiden Funktionstypen ganzrationale Funktionen sind. Beispielsweise:
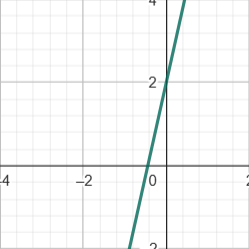
lineare Funktion: f(x) = 4,5 • x + 2
- f ( 3,21 ) = 16,445
- f ( -7 ) = -29,5
- f (0,5 ) = 4,25
quadratische Funktion: f(x) = 4x^2
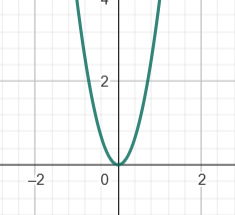
- f ( -3 ) = -36
- f (0,75) = 2,25
- f ( π ) = 39,4784
e-Funktionen
E-Funktionen sind wie lineare und quadratische Funktionen, weil man dort reelle Zahlen einsetzt. Der Grund dafür ist, weil sie wie folgt definiert sind: D = R
Um es zu veranschaulichen, nutzen wir direkt mal ein Beispiel: f(x) = e^(x)
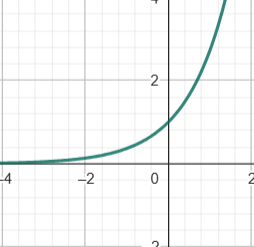
- e^( π ) = 23,1407
- e^(-2 ) = 0,1353
- e^( √2 ) = 4,1133
Logarithmusfunktion
Die Definitionsbereiche von Logarithmusfunktionen sind so definiert:
D = { x ∈ R | x > 0 }
Das bedeutet, dass der Definitionsbereich größer als null sein muss und nicht negativ sein darf! Zum Beispiel: f(x) = ln(x)
- ln ( 5 ) = 1,6094
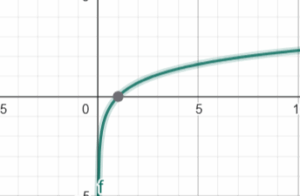
- ln ( 0 ) = mathematischer Fehler
- ln (-3 ) = mathematischer Fehler
Wann ln oder log benutzen?
- Bei einer 10er Basis auch “Zehnerlogarithmus” genannt benutzt man log oder auch abgekürzt lg.
- Bei einer Basis e, welches dann als “natürliches Logarithmus” bezeichnet wird nutzt man ln.
Wurzelfunktion
⇒ Wurzelfunktionen sind im Grunde nur umgewandelte Potenzfunktionen. Mehr dazu hier.
- Eine geradzahlige Wurzel wie eine “normale Wurzel ( √ )” kann nur eine beliebige positive reelle Zahl sein.
- Bei ungeradzahligen Wurzeln darf man alles, also irgendeine reelle Zahl, einsetzten.
Lösen wir gemeinsam die folgende Beispielaufgabe: f(x) = √(x-3)
x – 3 ≥ 0 | +3
x ≥ 3
⇒ D { x ∈ R | x ≥ 3 }
Das Ergebnis in der Wurzel muss null oder größer null sein, weil sonst ein mathematischer Fehler wäre. Wir lösen nur noch die Ungleichung nach x und dann haben wir schon unser Ergebnis.
Durch das Ergebnis bedeutet, dass alle reellen Zahlen erlaubt sind, aber nur unter der Bedingung, dass x größer oder gleich 3 ist.
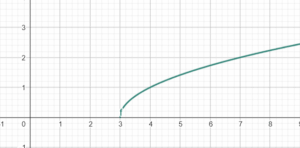
Es ist theoretisch nicht nötig, eine Aufgabe für ungeradzahlige Wurzeln zu lösen, da wir schon das Ergebnis kennen, denn das Ergebnis ist: D = R.
Definitionsbereich-Rechner Tipp
Falls du es ganz eilig hast und schnell einen Online-Rechner für Definitionsbereiche brauchst, dann kannst du gerne den Rechner von Wolfram|Alpha benutzen.
Quiz zu den Definitionsbereichen
Ergebnisse
#1. Was für ein Ergebnis haben lineare Funktionen?
#2. Was für ein Ergebnis haben geradzahlige Wurzelfunktionen?
#3. Was für ein Ergebnis haben e-Funktionen?
Ich hoffe der Artikel hat die geholfen die Definitionsbereiche verschiedenster Funktionen zu bestimmen und auch zu berechnen. Hinterlasse uns doch eine Bewertung und ein Kommentar, damit wir in Zukunft für dich bessere Artikel schreiben können.