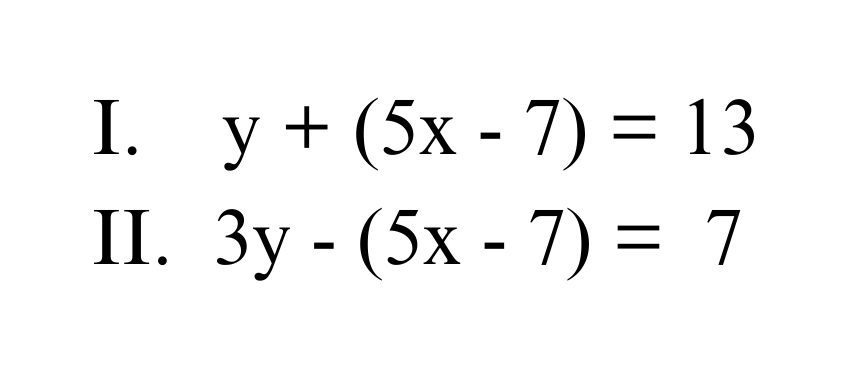(Noch keine Bewertungen)
Loading...
Das Additionsverfahren hast du im Unterricht kennengelernt, aber du hast noch Fragen? Kein Problem! Hier erklären wir dir alles, was du wissen musst.
Du wirst …
- lernen, wie du in 5 Schritten ein Gleichungssystem mit dem Additionsverfahren löst.
- verstehen, welche Lösungsmöglichkeiten gibt, wenn du das Verfahren nutzt.
- wissen, wann du das Subtraktions- oder Additionsverfahren anwenden kannst.
- dein Wissen direkt mit Hilfe von Übungsaufgaben testen können.
Bist du bereit? Dann starten wir!
1. Schritt: kleinstes gemeinsames Vielfaches
Zuerst suchst du das kleinste gemeinsame Vielfache von zwei Variablen. So kannst du sie später leichter “wegaddieren”.
Erinnerung:
Das kleinste gemeinsame Vielfache ist die kleinste Zahl, die ein Vielfaches beider der Zahlen ist.
Dafür nutzen wir direkt mal ein Beispiel:
I. 2x + 3y = 18 | • 3
II. 3x – 4y = -7 | • 2
I. 6x + 9y = 54
II. 6x – 8y = -14
Hier haben wir die x-Werte auf das gemeinsame Vielfache 6 gebracht.
(Tipp: Du kannst auch die y-Werte gleichsetzen- je nachdem, was einfacher ist.)
Achte darauf, dass alle Variablen aus der Zeile mit der Zahl malgenommen oder geteilt werden.
2. Schritt: Gleichungen addieren
Als nächstes geht’s ans Addieren. Unser Ziel ist es, eine der beiden Variablen zu entfernen. Damit das klappt, müssen sich die x-Werte oder y-Werte beim Addieren aufheben. In unserem Beispiel sind die x-Werte gleich (6x). Also ändern wir das Vorzeichen der zweiten Gleichung:
I. 6x + 9y = 54
II. 6x – 8y = -14 | • (-1)
Wir multiplizieren die zweite Gleichung mit -1, um die Vorzeichen zu ändern.
I. 6x + 9y = 54
II. -6x + 8y = 14
Jetzt rechnen wir die beiden Gleichungen zusammen. Infolgedessen können wir dann y ausrechnen.
3. Schritt: Variable in der Gleichung einsetzen
Nun setzt du y = 4 in eine der ursprünglichen Gleichungen ein. Zum Beispiel wird hier in die erste Gleichung eingesetzt:
2x + 3•4 = 18 ⇔ 2x + 12 = 18
In den nächsten Schritten werden wir diese Gleichung auflösen. Anschließend prüfen wir, ob die Lösung, die wir berechnet haben, auch richtig ist.
4. Schritt: Lösungsmöglichkeiten – mit Beispielen
Bevor wir weitergehen, werfen wir einen Blick auf unsere verschiedenen Lösungsmöglichkeiten.
Es gibt drei Lösungsmöglichkeiten bei einem linearen Gleichungssystem mit zwei Gleichungen: eine eindeutige Lösung, keine Lösung oder unendlich viele Lösungen.
Die beiden Gleichungen schneiden sich nur einmal.
Hierfür ist ein Beispiel dafür:
I. -6x + 5y = 15
II. 6x – 5y = -5
⇒ Die Geraden schneiden sich in dem Punkt S ( 2 | 1 ).
Die beiden Gleichungen verlaufen parallel und haben keinen Schnittpunkt.
Zum Beispiel:
I. -6x + 5y = 15
II. 6x – 5y = -5
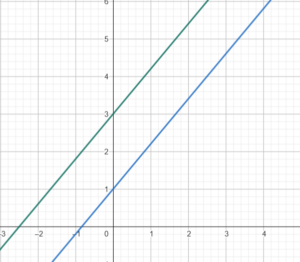
⇒ Folge: kein Ergebnis bzw. keinen Schnittpunkt
Die Geraden liegen aufeinander, sodass es unendlich viele Schnittpunkte.
Beispielsweise:
I. x – y = -1
II. 2x – 2y = -2
⇒ Alle Koordinatenpunkte der Gerade sind Lösungen. Folge: unendlich viele Ergebnisse.
Nun zurück zum Beispiel:
2x – 12 = 18 | – 12
⇔ 2x = 6 | ÷ 2
⇔ x = 3
Zunächst stellen wir die Gleichung um, sodass auf einer Seite nur Zahlen und auf der anderen nur Variablen sind. Anschließend dividieren wir durch 2 und lösen somit die Gleichung auf.
⇒ Ergebnis: L { 3 | 4 }
Nun kommen wir zum allerletzten Schritt, der dir hilft, auch in der Klassenarbeit oder in der Klausur eine gute Note zu garantieren.
5. Probe durchführen
Um sicherzustellen, dass unsere Lösung richtig ist, führen wir eine Probe durch. Wir setzten x und y in eine der ursprünglichen Gleichungen ein.
Unser Gleichungssystem war:
I. 2x + 3y = 18
II. 2x – 4y = -7
Unsere Ergebnisse waren:
x = 3
y = 4
Jetzt setzen wir die Werte ein!
2 • 3 + 3 • 4 = 18
6 + 12 = 18
18 = 18✔️
Die Probe zeigt, dass unsere Ergebnisse korrekt sind. Darüber hinaus wissen wir auch, dass unser lineares Gleichungssystem eine eindeutige Lösung mit nur einem Schnittpunkt hat.
Subtraktionsverfahren oder Additionsverfahren verwenden?
In der Regel solltest du das Additionsverfahren benutzen, wenn es bereits zwei gleiche Werte gibt, die sich direkt eliminieren lassen. Beispielsweise in der ersten Gleichung gibt es 2x und in der zweiten Gleichung -2x. Bei der Addition dieser Gleichungen wurden die Variablen sich dann gegenseitig entfernen. Die Vorzeichen dieser Werte sind also auch schon im besten Falle direkt unterschiedlich.
Bei dem Subtraktionsverfahren sollte man auch auf dasselbe achten. Aber Achtung! Hier sollten es die gleichen Vorzeichen sein, z. B.: 2x und 2x.
Trotzdem sollte man selbst entscheiden, was einem einfacher fällt und womit man besser arbeiten kann. Natürlich sollte man aber nur dann entscheiden, wenn in der Aufgabenstellung nach nichts Spezifischem gefragt ist.
Online-Rechner für das Additionsverfahren
Nach der Anleitung kennst du nun den Weg, um ein lineares Gleichungssystem mit dem Additionsverfahren zu lösen.
Nichtsdestotrotz willst du aber eine schnellere Überprüfung deines Ergebnisses?
Bei Mathepower findest du einen Online-Rechner. Damit löst du sogar dein lineares Gleichungssystem mit allen drei Verfahren: dem Gleichsetzungsverfahren, Additions- oder Subtraktionsverfahren.
So, das war’s mit dem Artikel zum Additionsverfahren. Jetzt bist du dran! Teste dein gelerntes Wissen direkt in einem kleinen Quiz. Danke fürs Lesen und viel Erfolg beim Üben! Wenn du schon fit im Additionsverfahren bist, hier geht es zum Gleichsetzungsverfahren.
Aufgaben zum Additionsverfahren
Ergebnisse
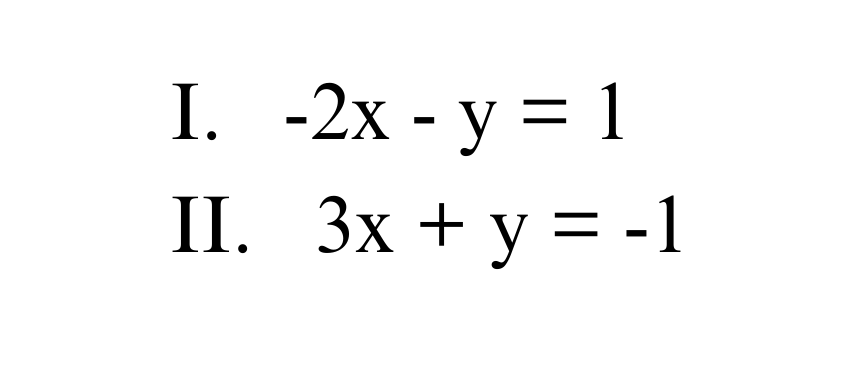
#1. Welche der drei Lösungsmöglichkeiten hat dieses Gleichungssystem?
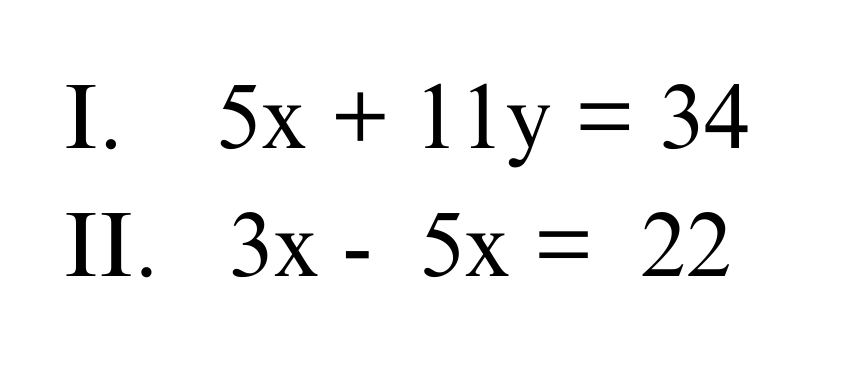
#2. Was ist das Ergebnis dieses Gleichungssystems?
