(Noch keine Bewertungen)
Loading...
Parabelfunktionen bereiten dir Probleme? Was ist der Unterschied zwischen allgemeiner Form und Scheitelpunktform? Kein Stress! Hier findest du all deine Antworten auf deine Fragen.
Hier wirst du… :
- die allgemeine Form und die Scheitelpunktform kennenlernen.
- wissen, wie die Verschiebung, Streckung oder Stauchung von quadratischen Funktionen funktioniert.
- dein Wissen anhand von Übungsaufgaben testen.
Schauen wir uns dann die Parabelfunktion genauer an. Bist du bereit? Los geht’s!
Arten von quadratischen Funktionen
Die Parabelfunktion ist eine quadratische Funktion, also eine Funktion zweiten Grades. Es gibt zwei Arten, wie man die quadratische Funktion notieren kann, und zwar in der allgemeinen Form und in der Scheitelpunktform. Fangen wir zuerst mit der allgemeinen Form an und dann gehen wir rüber zur Scheitelpunktform.
Allgemeine Form
Die allgemeine Form (Normalform) lautet: f(x) = ax^2 + bx + c
Diese Funktion allein sagt uns vieles darüber, wie die Parabelfunktion aussieht, ohne dass wir die Parabelfunktion gezeichnet haben.
- a bestimmt die Öffnung der Parabel. Also, wenn a negativ ist, ist die Funktion nach unten geöffnet, und wenn a positiv ist, ist die Funktion nach oben geöffnet.
- b sagt uns, ob die Parabel verschoben ist oder nicht. Wenn b negativ ist, verschiebt sich die Parabel nach rechts, und wenn b positiv ist, dann verschiebt sie sich nach links. Wie das genau funktioniert, wirst du gleich erfahren.
- c ist der y-Achsenabschnitt.
Quadratische Ergänzung
Wenn man bspw. die Normalform in die Scheitelpunktform umwandelt, braucht man die quadratische Ergänzung. Wie das funktioniert, sehen wir uns jetzt an. Bevor wir damit anfangen, solltest du die binomischen Formeln gut beherrschen.
1.Schritt: Ausklammern
f(x) = 5x^2 + 25x + 10
f(x) = 5 (x^2 + 5x + 2)
2.Schritt: Binomische Formel anwenden
f(x) = 5 (x^2 + 5x + 2)
f(x) = 5 (x^2 + 5x + 2,5^2 + 2)
f(x) = 5 (x + 2,5)^2 – 2,5^2 + 2)
Zuerst klammern wir die Zahl vor x^2 aus. Während wir das tun, müssen wir auch die anderen Zahlen geteilt durch 5 nehmen!
Hier musst du rückwarts die binomische Formel anwenden. Du musst nur die Funktion als Formel: (a^2 + 2ab + b^2) sehen. Da unser a^2=x^2 (a=x) und 2ab = 5x (2ab=2•2,5•x) ist, ist unser b^2=2,5^2.
1. Tipp
Um auf b zu kommen musst du nur geteilt durch 2 rechnen.
2. Tipp
Da wir 2,5^2 hinzugefügt haben, müssen wir es mit einem -2,5x^2 ausgleichen.
3.Schritt: Zahlen zusammenaddieren
f(x) = 5 (x + 2,5)^2 – 2,5^2 + 2)
f(x) = 5 (x + 2,5)^2 – 4,25
4.Schritt: Multiplizieren
f(x) = 5 (x + 2,5)^2 – 4,25
f(x) = 5 (x + 2,5)^2 – 21,25
Jetzt musst du nur die -2,5^2 und die 2 zusammenaddieren.
Zuletzt musst du nur die 5 mit der -4,25 multiplizieren, weil sie nicht mehr in der Klammer mehr ist.
Scheitelpunktform
Die Scheitelpunktform lautet: f(x) = a(x-d)^2 +e
Aufpassen auf das Vorzeichen von d!
Bspw. bei f(x) = a(x – d)^2 +e ist die Koordinate: S( d | e ). Natürlich auf genau umgekehrt, also f(x) = a(x + d)^2 +e und S( -d | e).
Im Folgenden werden wir die Scheitelpunktform in die allgemeine Form umwandeln. Wir nutzen am besten direkt das Beispiel von vorhin, um die Ergebnisse zu vergleichen.
1.Schritt: Binomische Formel anwenden
f(x) = 5 (x + 2,5)^2 -21,25
f(x) = 5 (x + 2,5)(x + 2,5) -21,25
f(x) = 5(x^2 + 5x + 2,5x^2) -21,25
2.Schritt: Ausklammern
f(x) = 5(x^2 + 5x + 2,5x^2) -21,25
f(x) = 5(x^2 + 5x + 6,25) -21,25
f(x) = 5x^2 + 25x + 31,25 -21,25
3.Schritt: Zahlen zusammenaddieren
f(x) = 5x^2 + 25x + 31,25 -21,25
f(x) = 5x^2 + 25x + 10
Zu Beginn musst du die binomische Formel anwenden. Bei diesem Beispiel ist es die erste binomische Formel.
Zunächst musst du ausklammern. Das machst du hier, indem du alles in der Klammer mit der Zahl 5 multiplizierst.
Im letzten Schritt musst du die Zahlen +31,25 und -21,25 miteinander addieren.
⇒ Die Ergebnisse der beiden Umwandlungen stimmen überein. Das bedeutet, dass unsere Ergebnisse richtig sind.
Verschiebung, Streckung, Stauchung
Um die Verschiebung einer Parabel zu ermitteln, braucht man nur den Scheitelpunkt. Bei der allgemeinen Form kann man dies auch nur anhand von b ermitteln. Wir wissen schon anhand des Vorzeichens, in welche Richtung die Parabel verschoben ist.
Dies machen wir mal mit dem Beispiel von vorhin:
f(x) = 5x^2 + 25x +10
Sx = -b ÷ 2a = -25 ÷ 2•5 = -25 ÷ 10 = -2,5
Sy = f(-2,5) = 5•(-2,5)^2 + 25•(-2,5) + 10
⇒ S( -2,5 | -21,25)
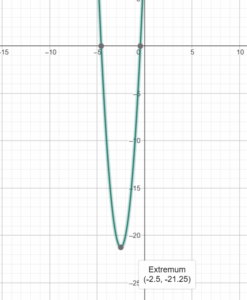
Aus der Parabelfunktion können wir ableiten, dass die Parabel 2,5 Einheiten nach links und 21,25 Einheiten nach unten verschoben ist.
Eine Parabel ist gestreckt, wenn |a| > 1 und gestaucht, wenn |a| < 1 ist.
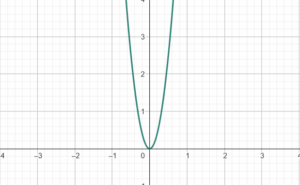
f(x) = 10x^2
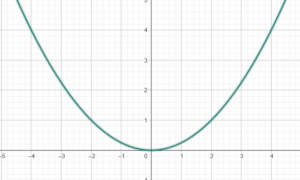
f(x) = 0,25x^2
Übungsaufgaben zur Umwandlung von allgemeiner Form in Scheitelpunktform
Übe das Umwandeln von allgemeiner Form in die Scheitelpunktform in beide Richtungen mit dem Klapptest von Materialen zum Selbstständigen Arbeiten.
Wir hoffen, dass der Artikel dir geholfen hat, die allgemeine Form sowie die Scheitelpunktform zu meistern.