Ihr behandelt in der Schule aktuell das Thema, wie man Brüche in Dezimalzahlen umwandelt, aber du blickst nicht durch? Keine Sorge!
In diesem Beitrag zeigen wir dir Schritt für Schritt…
- …wie du Brüche mit Zehnerpotenz, durch Erweitern/ Kürzen und durch Dividieren umwandeln kannst.
- …auf was du beim Umrechnen von negativen, gemischten und periodischen Dezimalbrüchen achten musst.
- …eine kompakte Übersicht der gängigen Brüche, die du dir merken solltest.
Am Ende findest du noch Übungsaufgaben mit Lösungen. Du wirst sehen: Es ist gar nicht so schwer, wie es vielleicht aussieht. Also starten wir!
Wenn du nun einen Bruch in eine Dezimalzahl, auch Dezimalbruch genannt, umwandeln möchtest, dann ist der erste Schritt zu identifizieren um welchen Bruch es sich handelt.
1. Fall: Bruch mit Zehnerpotenz (10, 100, 1000…) im Nenner (z.B. 34/100)
2. Fall: Bruch, dessen Nenner durch Erweitern (z.B. 3/25) oder Kürzen (z.B. 21/300) auf eine Zehnerpotenz gebracht werden kann
3. Fall: Bruch, dessen Nenner nicht auf eine Zehnerpotenz gebracht werden kann (z.B. 33/67)
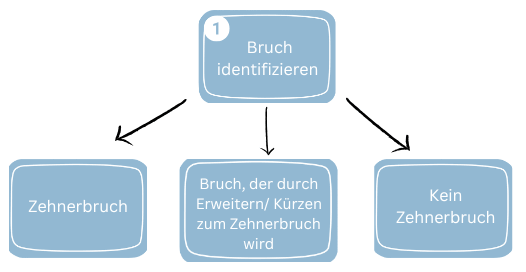
Je nach Art des Bruchs gibt es verschiedene Vorgehen. Insgesamt sind es drei Herangehensweisen, die du dir merken solltest.
1. Fall
Brüche mit Zehnerpotenz
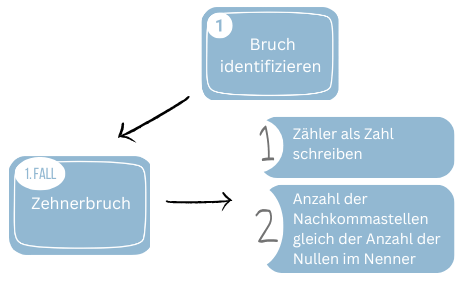
Um einen Zehnerbruch (z.B. 1/10, 47/100, 877/1000) in eine Dezimalzahl umzuwandeln, benötigst du nur zwei einfache Schritte:
Der Zähler ist die obere Zahl des Bruchs, der Nenner ist die Zahl unter dem Bruchstrich.
Wenn du noch mehr über das Bruchrechnen erfahren möchtest, dann schau dir gerne unseren Beitrag dazu an.
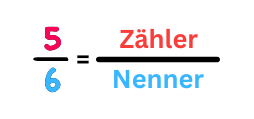
Beispiel: Bruch mit Zehnerpotenz
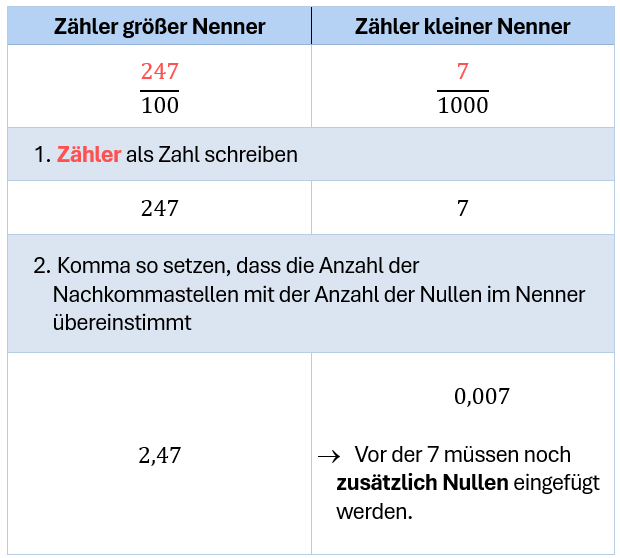
2. Fall
Brüche durch Erweitern oder Kürzen umrechnen
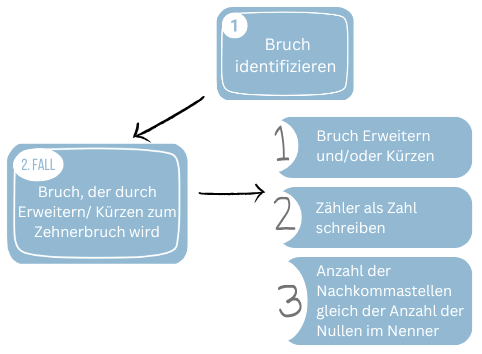
Nicht alle Brüche habe eine Stufenzahl (10,100,1000…) im Nenner. Allerdings lassen sich einige von diesen erweitern und/ oder kürzen, sodass man einen Zehnerbruch erhält. Danach kannst du mit den bekannten Schritten fortfahren.
Du brauchst also drei Schritte:
Beispiel: Bruch Erweitern

Beispiel: Bruch Kürzen

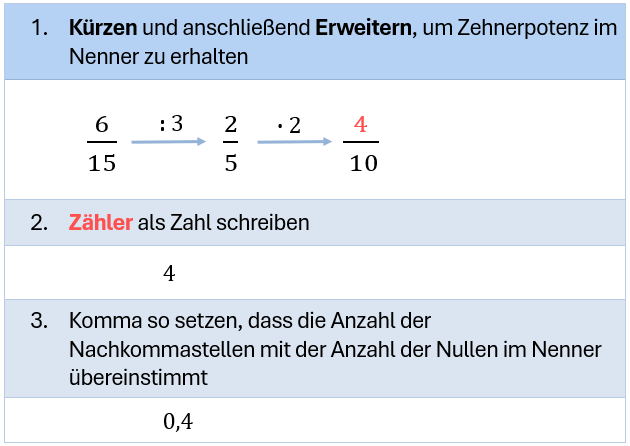
Beispiel: Bruch Kürzen und anschließend Erweitern
3. Fall
Bruch umwandeln durch Dividieren
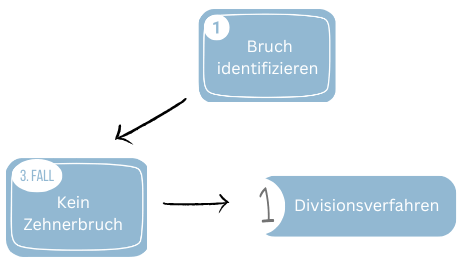
Wenn es nicht möglich ist den Nenner in eine Zehnerpotenz umzuwandeln, dann musst du den Zähler durch den Nenner dividieren.
Möchtest du gerne nochmal Schritt für Schritt erklärt bekommen, wie das schriftliche Dividieren funktioniert? Kein Problem, auch dazu haben wir einen Beitrag erstellt.
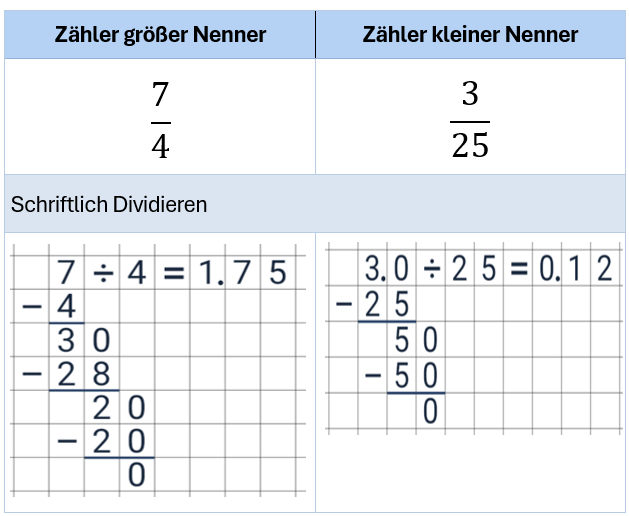
Beispiel: Kein Zehnerbruch
Brüche in Dezimalzahlen umrechnen: Besonderheiten negativer, gemischter und periodischer Brüche
Auch bei der Umwandlung von negativen, gemischten und unendlichen Brüchen in die Dezimalschreibweise kannst du die soeben gelernten Methoden anwenden.
Negative Brüche – Nur das Vorzeichen ändert sich
Bei negativen Brüchen ist es wichtig, dass du auch das Vorzeichen mit abschreibst.
Beispiel: negativer Zehnerbruch
-1/10 = -0,1
Gemischte Brüche
Gemischte Brüche sind solche, die eine ganze Zahl und einen Bruchteil enthalten (z.B. 2 3/4, 8 1/10).
Du gehst folgendermaßen vor:
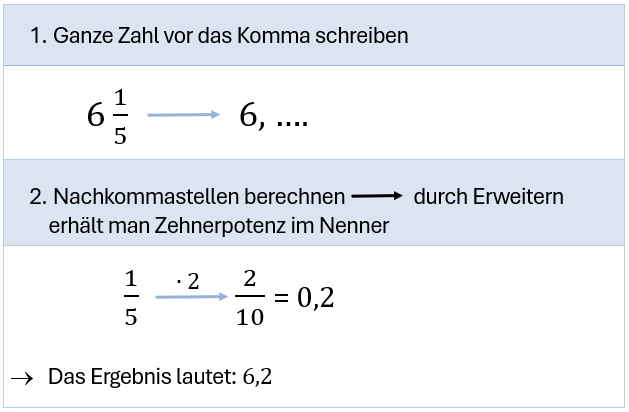
Beispiel: Gemischter Bruch mit Zehnerpotenz
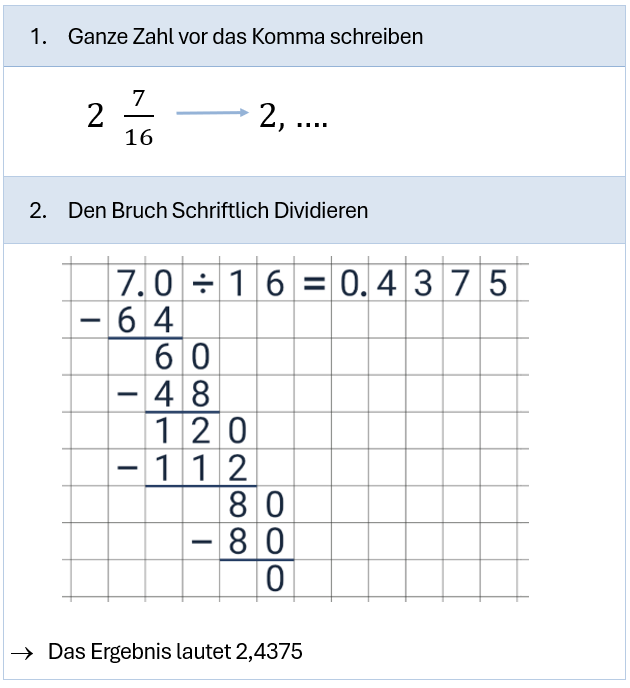
Beispiel: gemischter Bruch, dessen Nenner keine Zehnerpotenz ist und auch nicht durch Kürzen/ Erweitern zu einer Stufenzahl wird
Periodische Brüche unkompliziert lösen
Jeder Bruch kann in Dezimalschreibweise umgewandelt werden. Dabei unterscheidet man zwischen:
1. Endliche Dezimalzahlen: Brüche, die nach vollständiger Kürzung nur noch die Primfaktoren 2 und/oder 5 im Nenner enthalten.
- 7/8 = 0,875 (Nenner: 2 x 2 x 2)
- 3/10 = 0,3 (Nenner: 2 x 5)
2. Unendliche Dezimalzahlen: Brüche, deren Nenner andere Primzahlen außer 2 und/ oder 5 enthält. Wiederholt sich in einem unendlichen Dezimalbruch eine Zifferngruppe immer wieder, so bezeichnet man diesen als periodisch. Die Periode wird durch einen Strich über den Zahlen angezeigt.
Beispiel 1
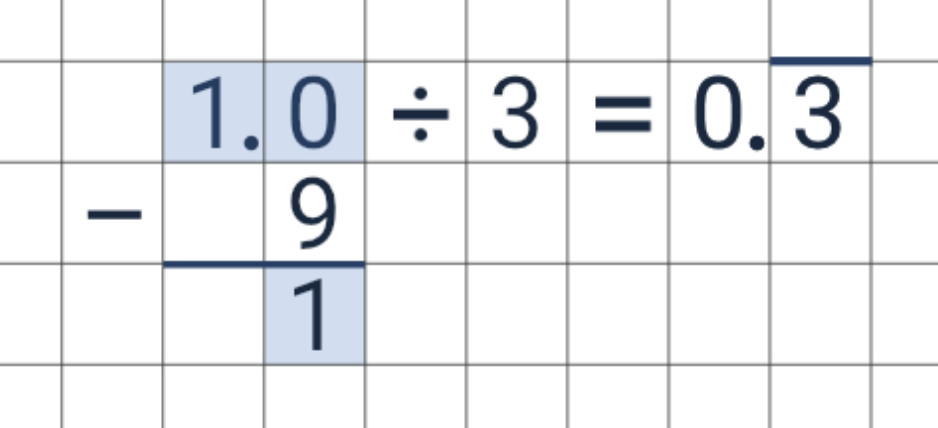
Man spricht: Null Komma Periode 3
Beispiel 2

Man spricht: Null Komma eins Periode sechs
Gängige Brüche in Dezimalzahlen umwandeln – eine Übersicht zum raschen Einprägen
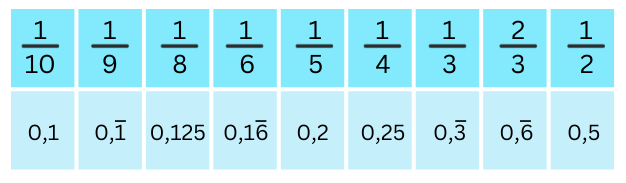
Bruch in Dezimalbruch umwandeln – 10 Übungen zu allen Vorgehensweisen
1. Aufgabe: -3/10
Vorgehen: Zehnerbruch
Beachte: negatives Vorzeichen abschreiben
Ergebnis: -0,3
2. Aufgabe: 3/8
Vorgehen: schriftliches Dividieren
Ergebnis: 0,375
3. Aufgabe: 1 1/4
Vorgehen: durch Erweitern (•25) Zehnerpotenz erhalten → 25/100
Beachte: ganze Zahl vor das Komma (1)
Ergebnis: 1,25
4. Aufgabe: 2/3
Vorgehen: schriftliches Dividieren
Beachte: (rein)periodischer Bruch
Ergebnis: ![]()
5. Aufgabe: 11/6
Vorgehen: schriftliches Dividieren
Beachte: gemischt periodischer Bruch
Ergebnis: ![]()
6. Aufgabe: 49/70
Vorgehen: durch Kürzen Stufenzahl im Nenner erhalten (:7) → 7/10
Ergebnis: 0,7
7. Aufgabe: -12/15
Vorgehen: erst Kürzen (:3), dann Erweitern (•2), um Zehnerbruch zu erhalten → 8/10
Beachte: negatives Vorzeichen abschreiben
Ergebnis: -0,8
8. Aufgabe: 5 4/5
Vorgehen: durch Erweitern (•2) Zehnerpotenz erhalten → 8/10
Beachte: ganze Zahl vor das Komma (5)
Ergebnis: 5,8
9. Aufgabe: 72/48
Vorgehen: erst Kürzen (:24), dann Erweitern (•5), um Zehnerbruch zu erhalten → 15/10
Ergebnis: 1,5
10. Aufgabe: 4/200
Vorgehen: Kürzen (:2), um Zehnerpotenz zu erhalten → 2/100
Ergebnis: 0,02
Wenn du wissen willst, wie das Umwandeln von Dezimalzahlen in Brüche funktioniert, dann schau gerne bei unserem Beitrag zu Dezimalzahlen vorbei!


