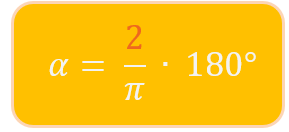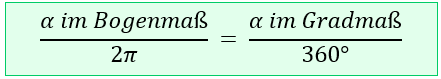5,00 von 5 Sterne
Loading...
Ihr habt in der Schule gerade mit Trigonometrie begonnen? Dabei habt ihr das Bogenmaß, Gradmaß und die Bogenlänge behandelt? Aber so richtig verstehst du nicht, was diese Begriffe beschreiben und wie du sie anwendest?
Kein Problem, wir erklären dir Step-by-Step alles Wichtige rund um das Winkelmaß.
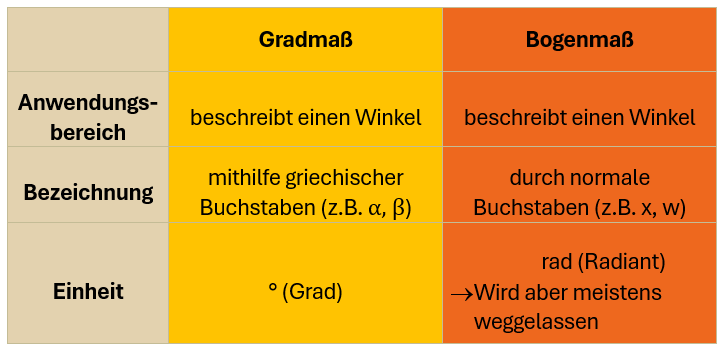
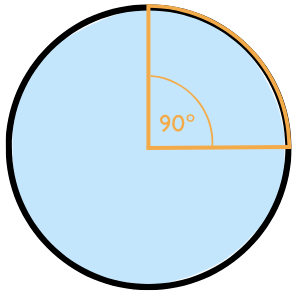Bisher haben wir Winkel mithilfe des Gradmaßes beschrieben. Ein rechter Winkel hat zum Beispiel 90°.
Du möchtest mehr über die verschiedenen Winkelarten erfahren? Dann schau dir gerne unseren Beitrag dazu an!
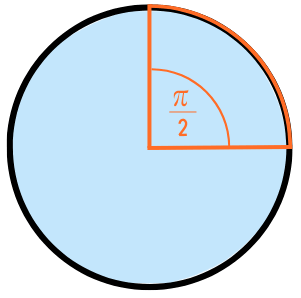Das Bogenmaß beschreibt genau wie das Gradmaß einen Winkel. Allerdings wird es nicht in Grad angegeben, sondern nur mit einer Zahl. Ein rechter Winkel entspricht beispielsweise einem Wert im Bogenmaß von π/2.
Wenn du wissen willst, was π eigentlich ist, dann schau dir gerne unseren Beitrag zur Zahl Pi an!
Beide Maße beschreiben einen Winkel also anteilig am gesamten Kreis. Nur ihre Bezugsgröße ändert sich.
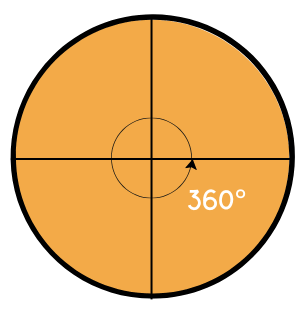
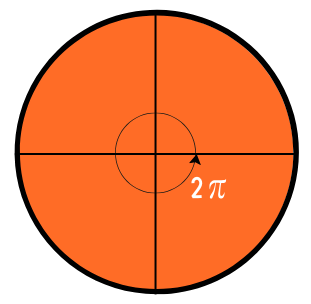
Das Gradmaß bezieht sich auf die 360°, wohingegen sich das Bogenmaß auf den Kreisbogen bezieht, welcher insgesamt 2π beträgt beim Einheitskreis.
Bogenmaß in Gradmaß – mit dieser Formel kein Problem
Das Bogenmaß lässt sich berechnen durch die Formel:
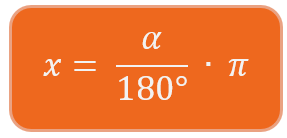
Hast du bereits den Wert im Bogenmaß angegeben und möchtest den Winkel in Grad erhalten, dann musst du die Formel nach α umstellen:
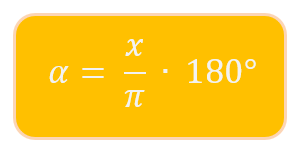
Schritt für Schritt Anleitung zum Umrechnen
Beispiel: von Grad ins Bogenmaß
Rechne α = 20° ins Bogenmaß um.
Wie gesagt, kannst du beide Formeln verwenden. Allerdings ist es einfacher, die Formel, die bereits nach der fehlenden Variable aufgelöst ist, zu benutzen.
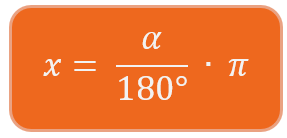
Da der Winkel in Grad angegeben ist, setzt du den Wert für Alpha in den Zähler ein.
Jetzt musst du die Gleichung nur noch ausrechnen.
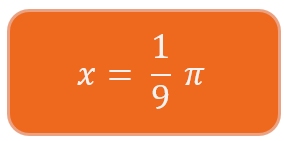
Beispiel: vom Bogenmaß ins Gradmaß
Forme x = 2 ins Gradmaß um.
α ≈ 114,591…°
⇒ α = 114,59°
Beziehung zwischen Bogenmaß und Gradmaß
Wenn du einen Wert im Bogenmaß mit einem Wert in Grad vergleichen möchtest, dann musst du die gerade aufgeführten Formeln gleichsetzen.
Für den Zusammenhang von Gradmaß und Bogenmaß gilt also:
Unterschied zwischen Bogenmaß und Gradmaß
Bogenlänge
Die Bogenlänge wird bestimmt durch:
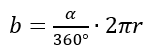
Bei einem Einheitskreis mit dem Radius 1, hat ein 180° Winkel also eine Bogenlänge von π.
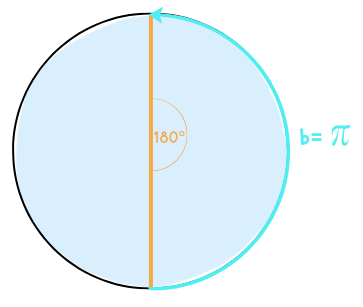
Wenn du die Formel des Bogenmaßes mit der Formel der Bogenlänge vergleichst, wirst du feststellen, dass sie bis auf die Variable „r“ gleich sind.
Für das Bogenmaß spielt der Radius also keine Rolle. Für die Bogenlänge hingegen schon.
Zusammenhang zwischen Bogenmaß und Bogenlänge
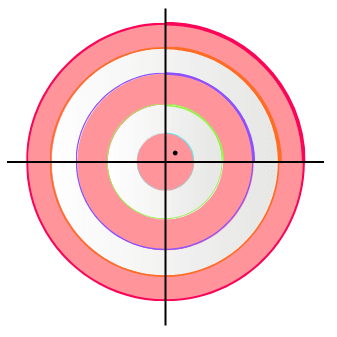
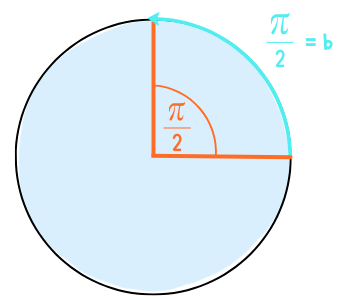
Das Bogenmaß ist ein Maß für einen Winkel. In dem Fall betrachten wir einen 90° Winkel. Der Winkel hat also den Wert π/2 im Bogenmaß.
Wie du erkennen kannst, hat der Winkel immer 90° egal wie groß der Kreis ist.
Die Bogenlänge hingegen verändert sich mit dem Radius. Wird der Kreis größer, wird auch die Bogenlänge größer.
Bogenmaß am Einheitskreis
Ein Einheitskreis ist ein Kreis mit dem Radius 1 Längeneinheit. Dieser hat somit den Umfang 2π. Die Besonderheit ist, dass in so einem Kreis das Bogenmaß eines Winkels mit der entsprechenden Bogenlänge übereinstimmt.
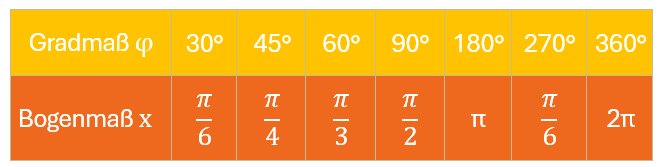
Winkelmaß Tabelle – wichtige Werte auf einen Blick
Übungsaufgaben zur Umrechnung von Bogenmaß in Grad und andersrum
1. Aufgabe: Rechne den Winkel α = 32° ins Bogenmaß um
Lösung:
1. Schritt: Formel aufstellen
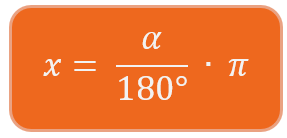
2. Schritt: α = 32° einsetzen
3. Schritt: Bogenmaß ausrechnen
x ≈ 0,5585…
⇒x = 0,56
2. Aufgabe: Forme den Winkel x = 6,2 ins Gradmaß um
Lösung:
1. Schritt: Formel aufstellen
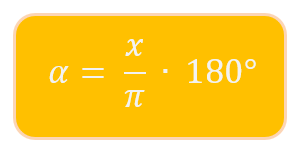
2. Schritt: x = 6,2 einsetzen
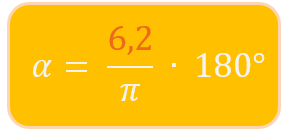
3. Schritt: Gradmaß ausrechnen
α ≈ 355,2338…
⇒ α = 355, 23°
3. Aufgabe: Schreibe den Winkel α = 234° im Bogenmaß
Lösung:
1. Schritt: Formel aufstellen
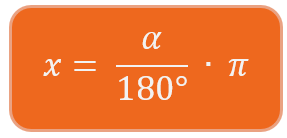
2. Schritt: α = 234° einsetzen
3. Schritt: Bogenmaß ausrechnen
x ≈ 4,0840…
⇒ x = 4,08
4. Aufgabe: Wandle den Winkel x = 1,7 in Grad um
Lösung:
1. Schritt: Formel aufstellen
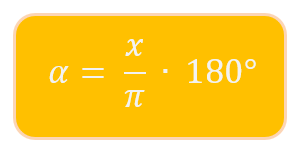
2. Schritt: x = 1,7 einsetzen
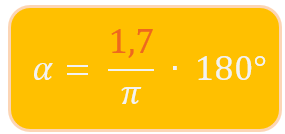
3. Schritt: Gradmaß ausrechnen
α ≈ 97,4028…
⇒ α = 97, 40°
Ihr beschäftigt euch in der Schule schon länger mit der Trigonometrie? Dann hast du mit Sicherheit auch schon von den trigonometrischen Funktionen gehört. Sinus, Cosinus und Tangens können am Anfang erstmal verwirrend sein. Wenn es dir auch so geht, dann schau dir gerne unseren Beitrag an!