(Noch keine Bewertungen)
Loading...
Dieser Artikel erklärt dir alles Wichtige rund um die Stammfunktion. Du lernst, was sie ist, wie du sie für verschiedene Funktionen bilden kannst und warum die Konstante C so wichtig ist. Das alles wird anschaulich mit vielen Beispielen dargestellt.
Das erwartet dich:
- Eine klare Definition: Was ist die Stammfunktion F(x)?
- Die wichtigsten Regeln zum “Aufleiten” (Integrieren).
- Konkrete Rechenbeispiele für Potenz-, e-, Wurzel- und Bruchfunktionen.
Lass uns loslegen!
Die Stammfunktion, meistens F(x) genannt, ist ein zentrales Thema der Integralrechnung und ist für eine reelle Funktion f(x) definiert. Sie ist quasi die Umkehrung der Ableitung.
Stell dir vor, du hast eine Funktion f(x). Die Stammfunktion F(x) ist dann diejenige Funktion, deren Ableitung wieder f(x) ergibt.
Die Stammfunktion hilft dir, eine Funktion zu berechnen und grob zu zeichnen.
Mathematisch ausgedrückt ist das die wichtigste Regel: 
In der Praxis ist das extrem nützlich, wenn du eine Änderungsrate (also die Ableitung) kennst und auf die ursprüngliche Funktion schließen möchtest.
Sie ist für dich in der Praxis sehr nützlich, wenn du nur die Ableitung kennst und auf die ursprüngliche Funktion schließen möchtest. Man verwendet für die Stammfunktion immer Großbuchstaben. Jede stetige Funktion besitzt eine Stammfunktion.
Stammfunktion bilden: Die wichtigsten Regeln und Formeln
Das Bilden der Stammfunktion nennt man integrieren oder umgangssprachlich auch aufleiten. Der Hauptgedanke dabei ist immer die Frage: “Welche Funktion 
muss ich ableiten, um 
zu erhalten?”
Eine Funktion hat nicht nur eine, sondern unendlich viele Stammfunktionen. Diese unterscheiden sich aber immer nur durch eine addierte Zahl, die man als Integrationskonstante 
bezeichnet. Das liegt daran, dass eine einfache Zahl beim Ableiten immer wegfällt.
Wichtige Regel: Beim Bilden einer Stammfunktion (unbestimmtes Integral) musst du immer die Integrationskonstante + am Ende hinzufügen. Die korrekte Stammfunktion von 
ist also 
.
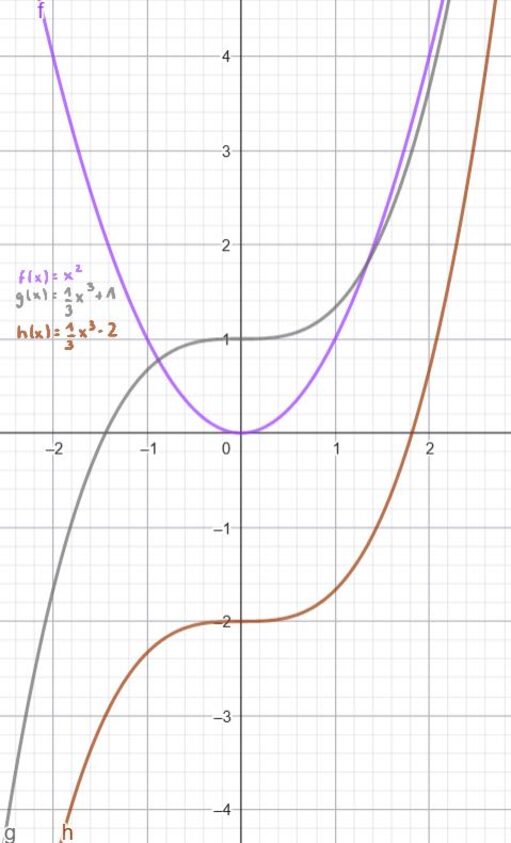
Als Beispiel zeigen wir dir verschiedene Stammfunktionen zu der Funktion . Die eine hat die Konstante 
und die andere 
Stammfunktion ableiten – Die Probe
Um sicherzustellen, dass du die Stammfunktion richtig gebildet hast, kannst du die Lösung ganz einfach überprüfen: Leite die von dir gefundene Stammfunktion einfach ab. Wenn das Ergebnis wieder die ursprüngliche Funktion ist, dann hast du richtig integriert. Dieses Vorgehen gilt als wichtige Probe und zeigt den umgekehrten Zusammenhang zwischen Ableiten und Integrieren.
Wichtige Stammfunktionen im Überblick
Damit du das ganze besser nachvollziehen kannst, erklären wir dir das ganze noch einmal an Hand von ein paar Beispielrechnungen. Denn nicht für jede Funktion lassen sich die Stammfunktionen so einfach ablesen, wie bei der Funktion aus dem Graphen.
Stammfunktion von e-Funktion
Wie du noch von der Ableitung der Eulerschen Zahl weißt, ist das ganze sehr simpel. Denn diese ist einfach nur die Funktion selbst:
Für das Integral der natürlichen Exponentialfunktion musst du zur Funktion ex noch die Konstante c dazu addieren.
Damit ist die Stammfunktion von e-Funktion direkt 
. Allgemeiner (umgekehrte Kettenregel) gilt 
; für 
also 
.
Stammfunktion lnx – so bestmmst du den natürlichen Logarithmus
Im Vergleich zur e Funktion lässt sich das Integral für den natürlichen Logarithmus nicht ganz so leicht bestimmen. Diese hat die folgende Form und lässt sich nur durch partielle Integration bestimmen:
Stammfunktion von Wurzel x und anderen Wurzelfunktionen
Auch für die Quadratwurzel kannst du das Integral bilden. Es gilt:
Daraus kannst du die folgende Stammfunktion herleiten:
Damit das alles noch anschaulicher wird und du sehen kannst, dass das auch analog für jede n-te Wurzel funktioniert, zeigen wir dir folgendes Beispiel:
![$$ \sqrt[3]{x^4}=x^\frac{4}{3}$$](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-501272225e0364479e8a2604720df0a4_l3.png "Rendered by QuickLaTeX.com")
![$$ \int \sqrt[3]{x^4}dx = \int x^\frac{4}{3}dx = \frac{3}{7}x^\frac{7}{3}$$](https://www.nachhilfe-team.net/lernen-leicht-gemacht/wp-content/ql-cache/quicklatex.com-37321513b90ee222578a5f5187f9e0e2_l3.png "Rendered by QuickLaTeX.com")
Stammfunktion Potenzfunktion: Die Formel für xⁿ
Die Stammfunktion-Formel für Potenzen lautet:
Den Rechenweg für das Integral einer Potenzfunktion 
kannst du dir sehr einfach merken:
Wir veranschaulichen dir das Ganze mal an einem Beispiel. Stell dir vor, dass die Stammfunktion von 
gesucht wird. Du suchst also F(x), was abgeleitet ergibt.
Wie du sehen kannst, wird am Ende die Konstante c eingefügt. Diese könnte 3, 6 oder 100 sein und es würde durch das Ableiten immer unser f(x) rauskommen.
Stammfunktion von 1/x und anderen Brüchen bestimmen
Möchtest du die Berechnung für einen Bruch durchführen, ist das ganz leicht, wenn du die Funktion in eine Potenzfunktion mit negativem Vorzeichen umschreibst. Damit das ganze anschaulich ist, zeigen wir dir das Ganze direkt an einem Beispiel:
Du musst dir merken, dass die Stammfunktion von 1/x eine Ausnahme darstellt. Denn würdest du die Regel von oben befolgen, hättest du eine 0 im Exponenten, was natürlich falsch wäre. Deshalb greift in diesem Fall die logarithmische Integrationsregel:
Stammfunktion Tabelle: Die wichtigsten Stammfunktionen zusammengefasst
| Funktion f(x) | Stammfunktion F(x) | Bedingungen / Hinweise |
 |
 |
Potenzregel; n ≠ -1 |
 |
 |
Ausnahme zur Potenzregel; x ≠ 0 |
 |
 |
e-Funktion |
 |
 |
a ≠ 0 (umgekehrte Kettenregel) |
 |
 |
Partielle Integration; x > 0 |
 |
 |
Potenzregel |
 |
 |
Beispiel Bruchpotenz |
 |
 |
Negativer Exponent |
 |
 |
Logarithmische Integrationsregel; f(x) ≠ 0 |
Stammfunktion bestimmen online – Der Integralrechner
Hast du trotzdem noch Probleme oder möchtest gerne den ausführlichen Rechenweg sehen, wie das Integral gebildet wird? Dann nutz noch diesen Online Integralrechner!
