(Noch keine Bewertungen)
Loading...
Die Normalverteilung begegnet Schülern oft erstmals im Mathe- oder Statistikunterricht und sorgt schnell für Verunsicherung. Begriffe wie Dichtefunktion, Standardabweichung oder Tabelle wirken abstrakt, obwohl sie viele alltägliche Phänomene beschreiben.
Dieser Ratgeber zeigt dir verständlich und Schritt für Schritt, wie die Normalverteilung aufgebaut ist, wie man sie nutzt und warum sie in Statistik und Stochastik eine so zentrale Rolle spielt.
Die Normalverteilung in der Statistik beschreibt, wie sich Werte in großen Datenmengen verteilen. Typisch ist eine Häufung um einen zentralen Mittelwert, während extreme Abweichungen immer seltener auftreten.
In der Normalverteilung Stochastik wird dieses Modell verwendet, um Zufallsprozesse mathematisch zu beschreiben und Wahrscheinlichkeiten abzuschätzen. Sie bildet damit eine wichtige Brücke zwischen Theorie und Praxis.
Die Normalverteilung ist ein Modell – sie beschreibt die Realität sehr gut, aber nicht perfekt.
Normalverteilung Formel – einfach erklärt
Die Normalverteilung Formel verbindet Erwartungswert, Standardabweichung und Wahrscheinlichkeiten.
Sie wird genutzt, um rechnerisch genaue Aussagen zu treffen, ist aber im Schulalltag oft weniger wichtig als das Verständnis der Zusammenhänge.
Auch wenn die Formel kompliziert aussieht, steckt dahinter lediglich die Idee, Abweichungen vom Mittelwert zu gewichten.
In Prüfungen wird die Formel häufig vorgegeben.
Normalverteilung Dichtefunktion – mathematische Beschreibung
Die Normalverteilung Dichtefunktion ist eine mathematische Funktion, die die Form der Kurve exakt beschreibt. Sie beschreibt also exakt, wie hoch die Kurve an jeder Stelle ist. Sie selbst liefert keine Wahrscheinlichkeiten, sondern nur Wahrscheinlichkeitsdichten.
Erst durch das Berechnen von Flächen unter der Kurve entstehen konkrete Wahrscheinlichkeiten.
Normalverteilung berechnen – Schritt für Schritt
Beim Normalverteilung berechnen ist ein strukturierter Ablauf entscheidend. Wer die Schritte konsequent einhält, kommt auch bei komplexeren Aufgaben sicher zum Ergebnis.
Besonders wichtig ist es, sauber zwischen Originalwerten und standardisierten Werten zu unterscheiden.
Beim Normalverteilung berechnen gehst du systematisch vor:
- Erwartungswert bestimmen
- Standardabweichung festlegen
- Wert standardisieren
- Wahrscheinlichkeit aus der Tabelle ablesen
Ergebnis: Du erhältst die Wahrscheinlichkeit, dass ein Wert in einem bestimmten Bereich liegt.
Wert standardisieren
Um einen einzelnen Wert X vergleichbar zu machen, wird er standardisiert. Dafür nutzt man die Z-Formel:
Sie zeigt, wie viele Standardabweichungen ein Wert vom Mittelwert entfernt ist. Dieser standardisierte Wert lässt sich anschließend nutzen, um Wahrscheinlichkeiten aus der Z-Tabelle abzulesen.
Normalverteilung Erwartungswert – das Zentrum
Der Normalverteilung Erwartungswert ist der Dreh- und Angelpunkt der gesamten Verteilung. Er gibt an, welcher Wert langfristig zu erwarten ist, wenn ein Experiment sehr oft wiederholt wird.
Da die Kurve symmetrisch ist, teilt der Erwartungswert die Fläche exakt in zwei gleich große Hälften.
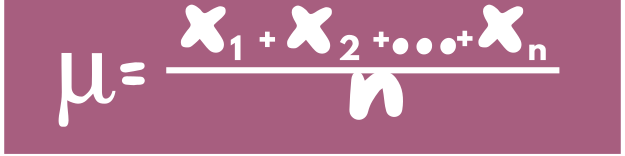
n= Gesamtanzahl der Werte
x= einzelner Wert
Falls du dein Wissen zum Erwartungswert vertiefen möchtest, haben wir auch einen Artikel dazu.
Normalverteilung Standardabweichung – Maß für Streuung
Die Standardabweichung der Normalverteilung zeigt, wie stark die einzelnen Werte um den Erwartungswert schwanken. Sie entscheidet darüber, ob die Glockenkurve schmal und steil oder breit und flach ist.
Zwei Datensätze können denselben Erwartungswert haben, sich aber stark in der Streuung unterscheiden.
Die 68-95-99,7-Regel der Normalverteilung: Rund 68 % der Werte liegen innerhalb einer Standardabweichung um den Erwartungswert μ, etwa 95 % innerhalb von zwei und 99,7 % innerhalb von drei Standardabweichungen.
Die Standardabweichung beeinflusst die Form der Kurve stärker als jeder andere Parameter.
Wenn du dein Wissen vertiefen möchtest, haben wir auch einen Artikel über die Standardabweichung.
Normalverteilung Varianz – mathematische Grundlage
Die Varianz der Normalverteilung wird vor allem in mathematischen Berechnungen verwendet. Sie ist notwendig, um Formeln kompakt darzustellen und weiterführende statistische Verfahren anzuwenden.
Für dich ist es meist ausreichend zu wissen, wie Varianz und Standardabweichung zusammenhängen.
Merke:
In Textaufgaben wird häufiger die Standardabweichung verwendet.
Falls du mehr über Varianz erfahren möchtest, haben wir auch dazu einen Artikel.
Normalverteilung Beispiele – aus dem Schulalltag
Normalverteilung Beispiele zeigen, wie praxisnah das Thema ist.
Diese Beispiele helfen, das abstrakte Modell mit realen Situationen zu verknüpfen.
Normalverteilung Beispiele machen das Thema greifbar:
- Körpergrößen in einer Klasse
- Punktzahlen in Klassenarbeiten
- Messfehler bei Experimenten
Erkenntnis: Je größer die Datenmenge, desto besser passt die Normalverteilung.
Normalverteilung Kurve – grafische Darstellung
Die Normalverteilung Kurve hilft dabei, Daten visuell zu verstehen. Sie macht sofort sichtbar, wo die meisten Werte liegen und wie stark sie streuen.
Besonders im Unterricht wird die Kurve genutzt, um Wahrscheinlichkeiten nicht nur zu berechnen, sondern auch zu „sehen“.
Beispiel: Die meisten Klassenarbeiten liegen nahe am Notendurchschnitt, sehr schlechte oder sehr gute Noten sind selten.
Normalverteilung Glockenkurve – typische Form
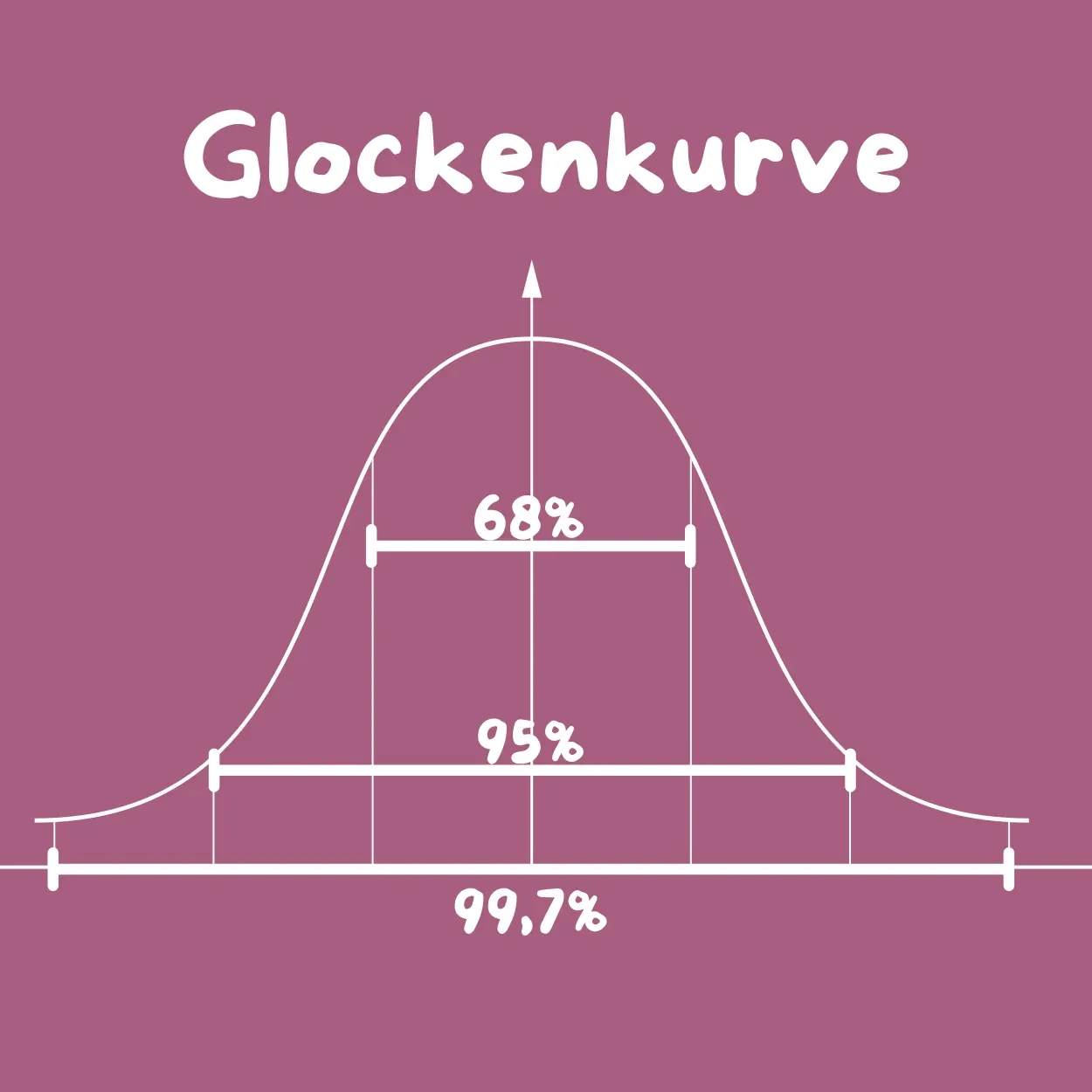
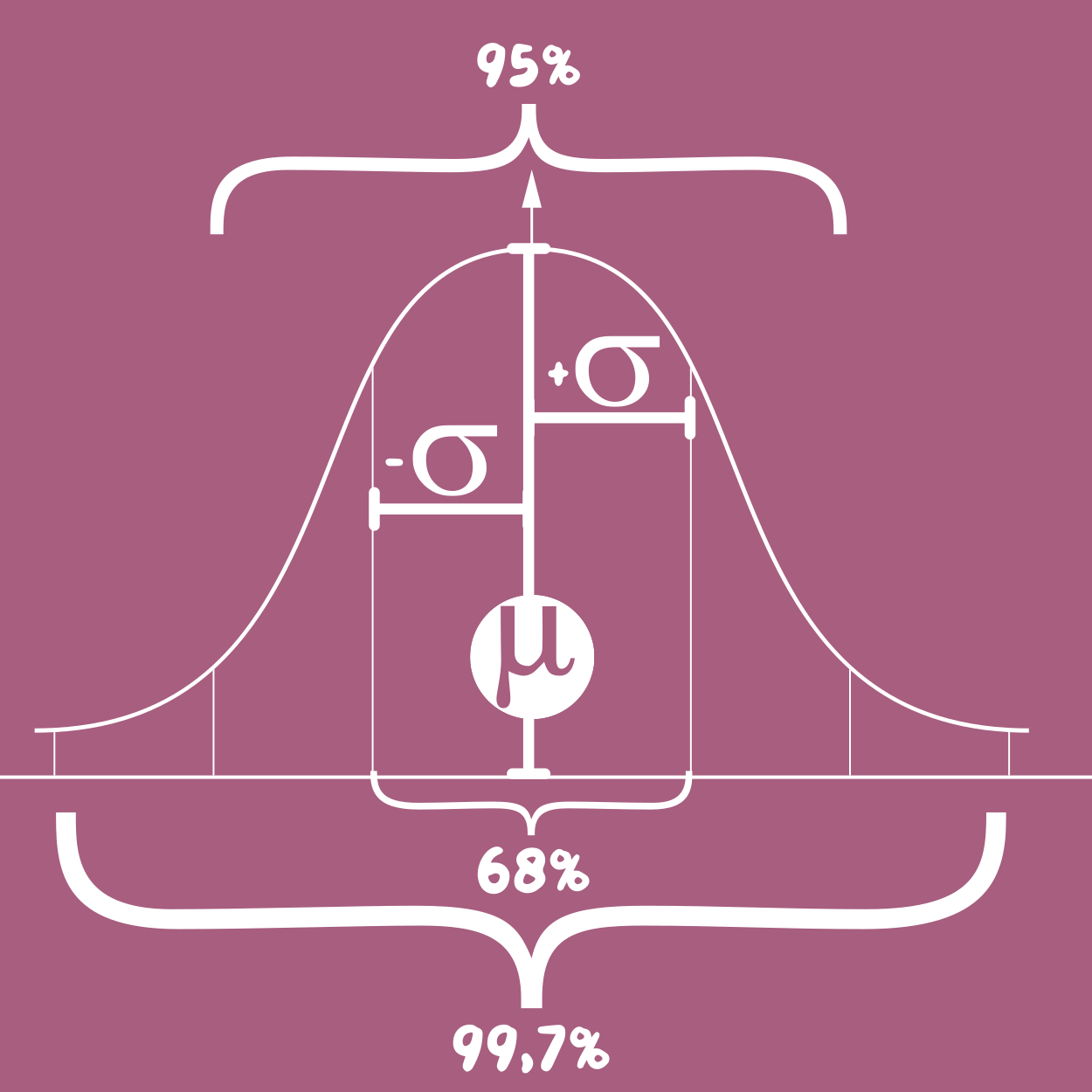
Die Normalverteilung Glockenkurve hat ihren Namen durch ihre charakteristische Form. Sie steigt gleichmäßig an, erreicht in der Mitte ihr Maximum und fällt danach symmetrisch wieder ab.
Diese Symmetrie sorgt dafür, dass Abweichungen nach oben und unten gleich wahrscheinlich sind.
Faustregel
- 68 % der Werte liegen innerhalb von ±1 Standardabweichung
- 95 % innerhalb von ±2
- 99,7 % innerhalb von ±3
Normalverteilung Tabelle – Wahrscheinlichkeiten ablesen
Die Normalverteilung Tabelle ist ein zentrales Hilfsmittel im Unterricht. Sie ermöglicht es, Wahrscheinlichkeiten schnell und zuverlässig zu bestimmen.
Dafür werden Werte zuerst standardisiert, sodass der Erwartungswert 0 und die Standardabweichung 1 beträgt.
Voraussetzung ist die Standardisierung, durch die alle Normalverteilungen vergleichbar gemacht werden.
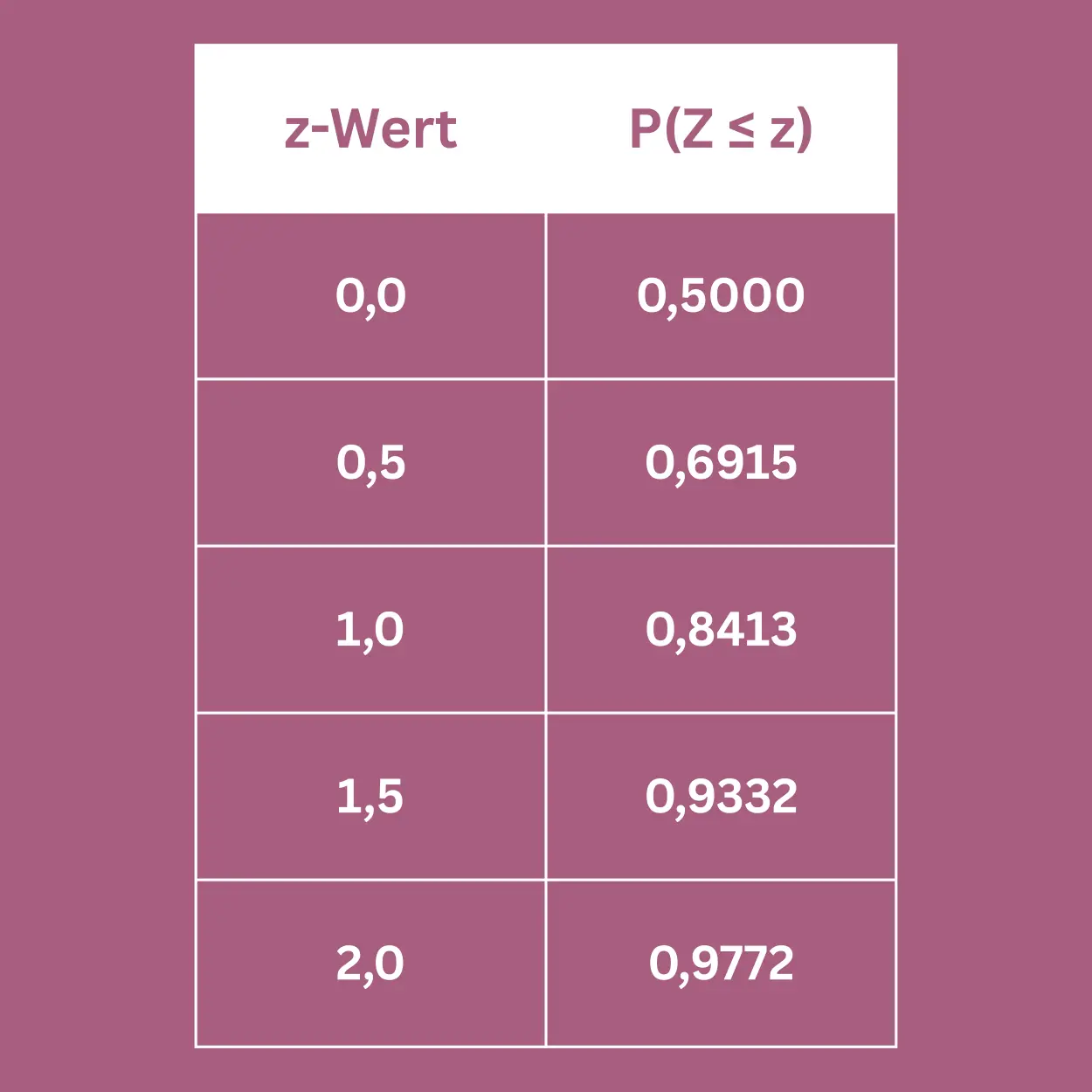
Die Tabelle zeigt die Wahrscheinlichkeit, dass ein Wert der Standardnormalverteilung kleiner oder gleich dem angegebenen z-Wert ist.
Beispiel:
Normalverteilung Aufgaben – typische Fragestellungen
In Normalverteilung Aufgaben geht es häufig um Anteile und Grenzwerte. Du sollst abschätzen, wie viele Werte in einem bestimmten Bereich liegen.
Solche Aufgaben fördern das Verständnis für Wahrscheinlichkeiten und statistisches Denken.
In Normalverteilung Aufgaben wird häufig gefragt:
- Wie groß ist die Wahrscheinlichkeit für Werte über/unter einem Grenzwert?
- Wie viele Schüler erreichen mindestens eine bestimmte Punktzahl?
. Hinweis: Zeichnungen sparen Zeit und reduzieren Fehler.
