Rechengesetze und Rechenregeln schnell beherrschen

Kennst du das? Du hast eine Matheaufgabe vor dir und weißt gar nicht, wo du anfangen sollst? Dafür gibt es eine einfache Lösung: die Rechengesetze. Sie machen dir das Rechnen leichter und helfen dir, die richtige Lösung zu finden – wenn du sie richtig anwendest.

Wir zeigen dir die wichtigsten Rechengesetze. Mit etwas Übung wirst du damit zum Mathe-Profi!

Was sind die Rechengesetze? – einfach erklärt

Im Matheunterricht wirst du von den Rechenregeln und Rechengesetzen nicht herumkommen, denn sie werden dir im Laufe deiner Schulzeit immer wieder behilflich sein.

Rechenregeln geben an, in welcher Reihenfolge die Rechenschritte bei einem Term durchgeführt werden müssen.

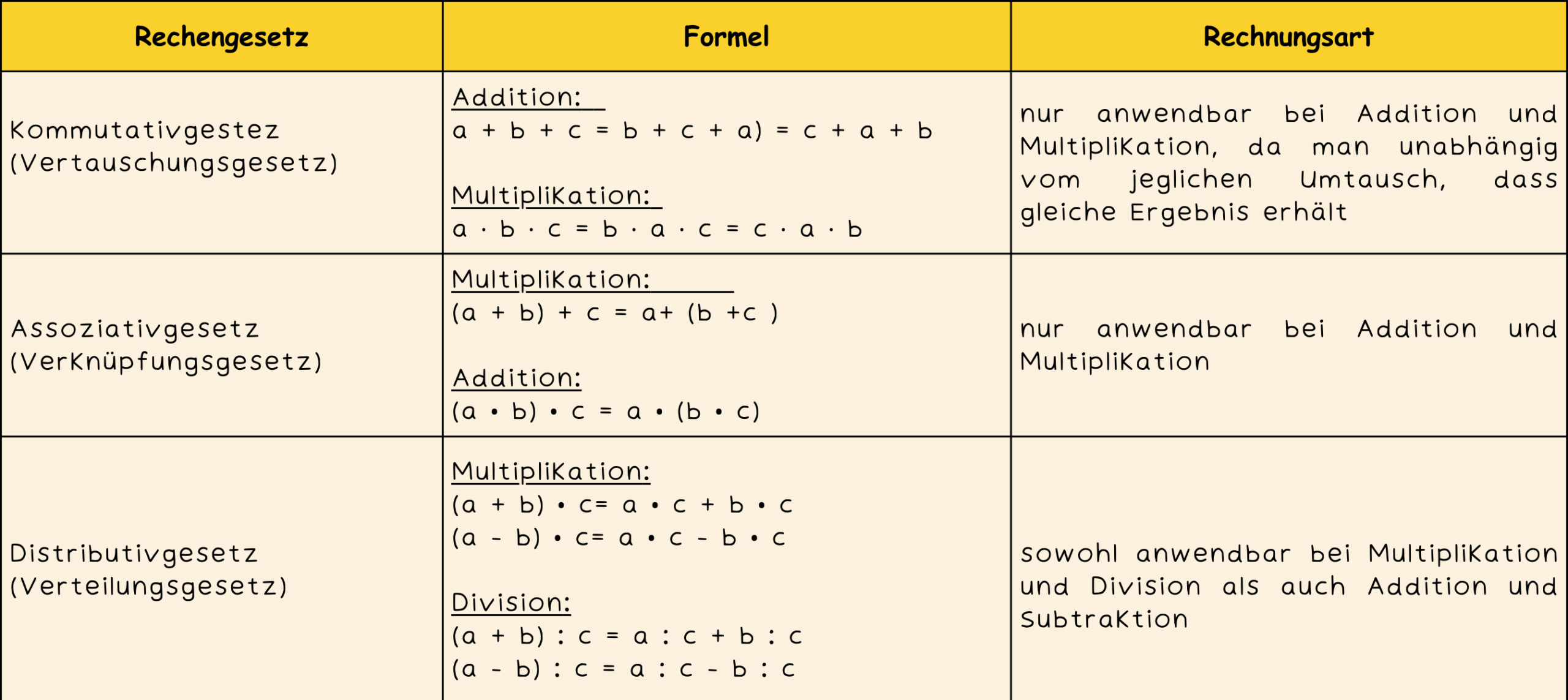
Rechengesetze sind feste Regeln in der Mathematik, die beschreiben, wie man Terme umformen oder vereinfachen kann. Dazu gehören das Kommutativgesetz, das Assoziativgesetz und das Distributivgesetz.

Damit du den Überblick behältst, schauen wir uns die Rechenregeln der Reihe nach an – von außen nach innen. Wir beginnen mit den Klammerregeln.

Rechenregeln – Vorrangregeln

Klammerregeln

Fangen wir mit der wichtigsten Rechenregel, der Klammerregel an:

Alles, was in Klammern steht, wird zuerst gerechnet.
 Egal, ob Plus, Minus, Mal oder Geteilt – wenn etwas in Klammern steht, musst du das zuerst erledigen.
In Mathe gibt es verschiedene Arten von Klammern, zum Beispiel:

( ) → runde Klammern
[ ] → eckige Klammern
{ } → geschweifte Klammern

Potenzregeln

Vielleicht hast du schon einmal eine Potenz gesehen – das ist eine kleine Zahl oben über einer anderen Zahl, wie zum Beispiel:

– das spricht man: drei hoch zwei.

Das bedeutet einfach: drei mal drei, also .

Falls du weiter in das Thema Potenzen eintauchen möchtest, wirf doch ein Blick in die Potenzgesetze.

Punkt-vor-Strichrechnung

Wenn du einen Term berechnest, musst du also zuerst alle Multiplikationen (·) und Divisionen (:) erledigen – und erst danach die Additionen (+) und Subtraktionen (–).

Rechengesetze

Kommutativgesetz

Eines der Rechengesetze ist das Kommutativgesetz, auch Vertauschungsgesetz bezeichnet, kannst du die Zahlen des Terms untereinander vertauschen, da gleichbedeutend, mit welcher Reihenfolge du die Zahlen berechnest, das gleiche Ergebnis herauskommt.

Beachte jedoch, dass das Kommutativgesetz nur bei Multiplikation und Addition funktioniert, da zum Beispiel nicht gleich ergibt.

Hierbei gilt:

Kommutativgesetz- Beispielaufgabe

Vielleicht fragst du dich: Warum sollte man Zahlen überhaupt vertauschen? Ganz einfach! Genau wie manche Leute lieber zuerst Müsli und dann Milch in ihre Schüssel geben, haben auch Menschen Vorlieben beim Rechnen.

Zum Beispiel berechnen manche Leute besser als .

Schauen wir uns das nochmal genauer mit zwei Beispielen an.

Assoziativgesetz

Ähnlich wie beim Kommutativgesetz, wird das Assoziativgesetz bzw. Verknüpfungsgesetz bei der Addition und Multiplikation angewendet. Es erlaubt dir, bei Termen mit mehr als drei Faktoren Klammern nach Belieben zu setzen.

Es gilt:

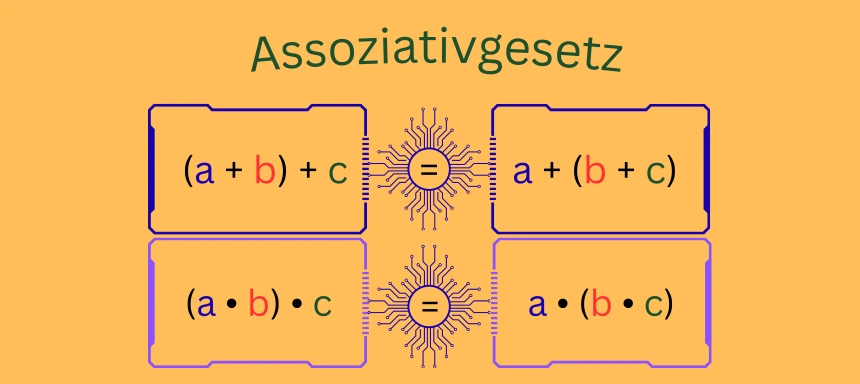
Assoziativgesetz Beispielaufgabe

Das Ziel beim Assoziativgesetz ist dir das Berechnen des Terms zu vereinfachen, indem du durch Klammern bestimmte Teile des Terms zuerst berechnest.

Hier sind zwei Beispiele:

Distributivgesetz

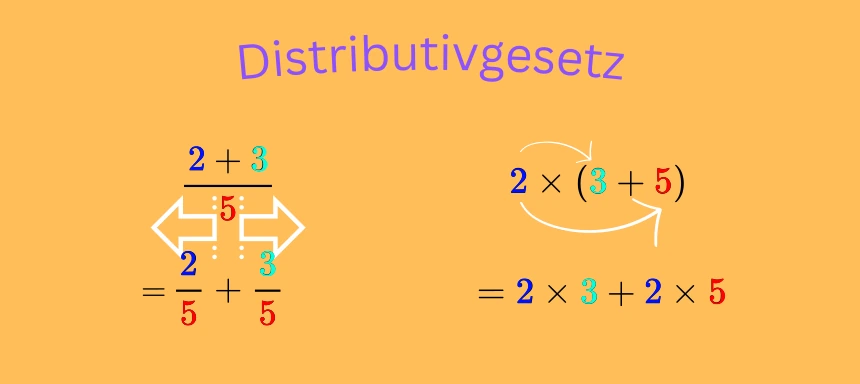
Als Nächstes kommen wir zum Distributivgesetz, auch unter der Bezeichnung Verteilungsgesetz bekannt.

Dieses Rechengesetz besagt, dass die Punktrechnung und die Strichrechnung verbindet werden, sodass du den Faktor vor der Klammer mit jeder Zahl in der Klammer berechnen kannst.

Dabei unterscheidet man das Distributivgesetz der Multiplikation und das Distributivgesetz der Division.

Distributivgesetz – Beispielaufgabe

Kommutativgesetz, Assoziativgesetz und Distributivgesetz auf einem Blick

Teste dich selbst!

FAQ