Was ist ein Fünfeck und warum ist es in der Geometrie so wichtig? In diesem Artikel erfährst du kurz und verständlich, welche Eigenschaften ein Fünfeck hat, wie du es zeichnest und wie du Schritt für Schritt den Flächeninhalt berechnest.
Legen wir los!
Ein Fünfeck ist eine geometrische Figur mit fünf Seiten und fünf Ecken. Es gehört zu den Vielecken (Polygonen) und kann in unterschiedlichen Formen auftreten, regelmäßig oder unregelmäßig. Bei einem regelmäßigen Fünfeck sind alle Seiten gleich lang und alle Innenwinkel gleich groß. Bei einem unregelmäßigen Fünfeck ist es genau andersrum.
Fünfeck Winkelsumme – einfach erklärt
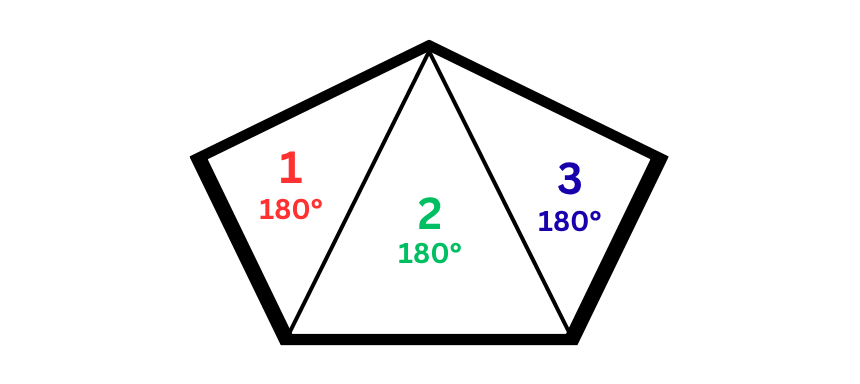
Die Winkelsumme eines beliebigen Fünfecks, egal ob unregelmäßig oder regelmäßig, beträgt 540°. Demnach sind alle Winkel 108°. Das liegt daran, dass man jedes Fünfeck in drei Dreiecke unterteilen kann, welche immer eine Winkelsumme von 180° haben.
Regelmäßiges Fünfeck Flächeninhalt berechnen – in 4 simplen Schritten
Um den Flächeninhalt zu bestimmen, brauchst du idealerweise eine dieser Größen:
- Seitenlänge a
- Umkreisradius R (der Abstand vom Mittelpunkt zu einem Eckpunkt)
- Inkreisradius r (der Abstand vom Mittelpunkt zur Seite)
Am gebräuchlichsten ist in der Schule oft die Seitenlänge a. Falls dies nicht der Fall ist, gibt es für die anderen Alternativen andere Formeln.
Für unser Beispiel nehmen wir eine Seitenlänge (a) von 4 cm.
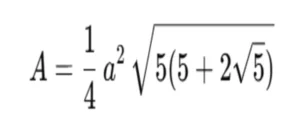
Schritt 1 - a² auflösen
4² = 16
Schritt 2 - Den Term im inneren der Wurzel ausrechnen
5 ![]()
![]()
(5 + 2 x 2,23607) = 9,47214
5 x 9,47214 = 47,3607
Schritt 3 - Wurzel ziehen
![]()
Schritt 4 - in die Formel einsetzen
![]() x 16 x 6,883 = 27,532 cm²
x 16 x 6,883 = 27,532 cm²
Unregelmäßiges Fünfeck Flächeninhalt berechnen
Bei unregelmäßigen Fünfecken ist ein Trick notwendig, um den Flächeninhalt zu berechnen. Wie wir bereits gelernt haben, kann man ein Fünfeck in mehrere Dreiecke unterteilen. Das kannst du nun hier nutzen, um auf den Flächeninhalt des unregelmäßigen Fünfecks zu kommen. Teile dazu das Fünfeck in mehrere sinnvolle Dreiecke, berechne deren Flächeninhalt und addiere diese zusammen. So hast du nun den Flächeninhalt des unregelmäßigen Fünfecks berechnet.
Wie du den Flächeninhalt der Dreiecke berechnest, erfährst du hier in einem unserer anderen Artikel.
Regelmäßiges Fünfeck zeichnen – so einfach geht es
Bei Aufgaben dieser Art ist in den meisten Fällen eine Seitenlänge gegeben. Diese Linie zeichnest du nun auf ein leeres Papier in die Mitte des Blattes.
In unserem Beispiel werden wir mit 4 cm Seitenlänge arbeiten.
Nun trägst du an beiden Enden der Linie einen Winkel von 54° an. Wenn du das erledigt hast, sollte nun ein Dreieck vor dir liegen.
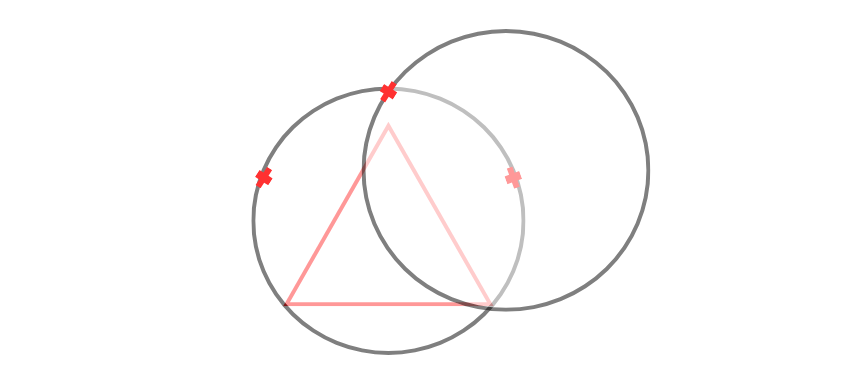
Als nächstes nimmst du deinen Zirkel, stichst diesen an der Spitze des Dreiecks ein und zeichnest einen Kreis, der die beiden anderen Eckpunkte des Dreiecks berührt.
Jetzt stichst du deinen Zirkel an dem rechten Eckpunkt des Dreiecks ein und zeichnest einen neuen Kreis, der den linken Eckpunkt des Dreiecks berührt.
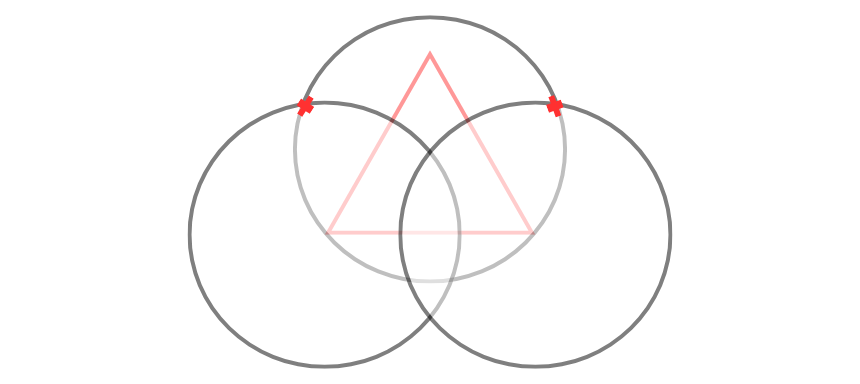
Beide Kreise sollten sich rechts oberhalb deines Dreiecks schneiden, markiere diesen Punkt.
Das Gleiche machst du jetzt mit dem linken Eckpunkt des Dreiecks.
Nun solltest du zwei markierte Stellen haben, wo sich deine Hilfskreise mit dem ersten Kreis geschnitten haben.
Der finale Schritt ist es, den Zirkel nun an dem rechten Schnittpunkt der beiden Kreise einzustechen und von da aus einen neuen Hilfskreis zu zeichnen, welcher den rechten Eckpunkt des Dreieckes berührt.
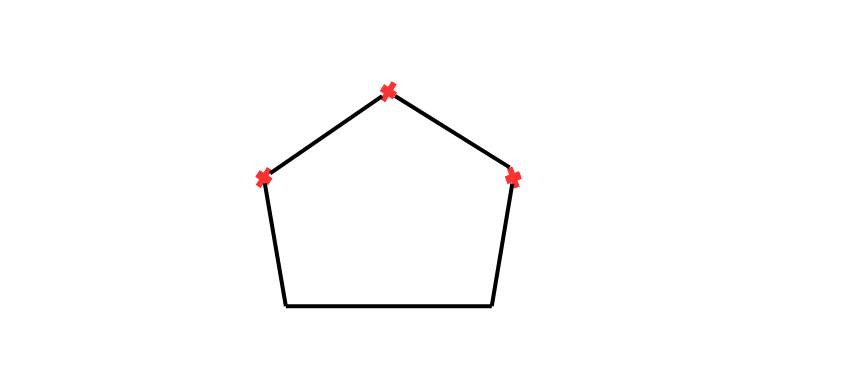
Jetzt hast du einen weiteren Schnittpunkt direkt oberhalb deines Dreiecks.
Wenn du nun die beiden unteren Eckpunkte deines Dreiecks mit den drei Schnittstellen deines Kreises verbindest, bildet sich dein regelmäßiges Fünfeck und du hast es geschafft!
Unregelmäßiges Fünfeck zeichnen
Ein unregelmäßiges Fünfeck kannst du nicht so einfach zeichnen. Dazu benötigst du alle Winkel und Seitenlängen. Wenn du diese hast, kannst du nach und nach die Seiten zeichnen und mit den passenden Winkeln verbinden.
Fünfeck mit einem rechten Winkel
Da die Winkelsumme eines Fünfecks immer 540° ergeben muss, ist es möglich, dass ein Fünfeck zwischen null und drei rechten Winkeln hat.