Brüche erweitern – Schritt für Schritt erklärt

Ob beim Teilen eines Kuchens oder beim Lösen von Matheaufgaben! Brüche erweitern hilft, sie vergleichbar zu machen und leichter zu rechnen. In diesem Artikel lernst du Schritt für Schritt, wie das ganz einfach funktioniert. Zusätzlich warten am Ende noch Übungsaufgaben, mit denen du dein erlerntes Wissen testen kannst.

Was ist ein Bruch?

Ein Bruch setzt sich aus zwei Zahlen zusammen: dem Zähler und dem Nenner, die durch einen waagerechten Bruchstrich voneinander getrennt sind. Die Zahl oberhalb des Bruchstrichs nennt man Zähler, die Zahl darunter Nenner. Der Bruchstrich zeigt an, dass der Zähler durch den Nenner geteilt wird (Division).

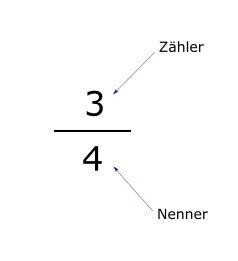
Wie erweitere ich Brüche?

Damit du besser verstehst, wie das Erweitern von Brüchen funktioniert, schauen wir uns das folgende Beispiel anhand eines Kuchen an:

Den Kuchen schneiden wir in 2 gleich große Stücke. Jedes Stück ist des Kuchens.

Jetzt erweitern wir diesen Bruch, indem wir die beiden Stücke noch einmal halbieren.

So entstehen 4 gleich große Stücke. Ein Stück der ursprünglichen Hälfte entspricht nun also 2 von 4 Stücken, also .

Zwar hat sich an der Menge des Kuchens nichts geändert. Trotzdem werden zwei verschiedene Brüche verwendet, die beide dasselbe meinen.

Das zeigt dir, dass und für die genau gleiche Menge an Kuchen stehen.

Brüche erweitern – Beispiel

Was ein Bruch ist und was es bedeutet, diesen zu erweitern, das weißt du jetzt. Nun lernst du in diesem Kapitel, wie genau du rechnen musst, um jede Aufgabe zu meistern.

Beispiel: Der Bruch soll mit 5 erweitert werden.

Um zur Lösung zu kommen, multiplizierst du sowohl den Zähler als auch den Nenner mit 5. Im Zähler rechnest du also 5 5 und im Nenner 20 5.

Achtung: Die 0 darf nie zum Erweitern genutzt werden.

Erweiterungszahl ermitteln – schnell und einfach

Dass die Erweiterungszahl vorgegeben ist, wird bei den meisten Aufgaben leider nicht der Fall sein. Um Brüche zu addieren und zu subtrahieren, müssen sie jedoch den gleichen Nenner haben. Daher erfährst du jetzt, wie du vorgehen musst, um die Erweiterungszahl zu finden.

Beispiel: Bringe die Brüche  und auf einen Nenner.

Du überlegst dir nun, mit welcher Zahl der kleinere Nenner 4 multipliziert werden muss, um auf den größeren Nenner 12 zu kommen. Da 4 3 = 12 ist, kannst du den ersten Bruch mit 3 erweitern und kommst so auf .

Tipp: Teilst du den größeren Nenner durch den kleineren, kommst du auch auf die Erweiterungszahl.

Brüche kürzen und erweitern

Beim Erweitern von Brüchen multiplizierst du Zähler und Nenner mit derselben Zahl. Brüche kürzen heißt, dass Zähler und Nenner durch die gleiche Zahl dividiert werden.

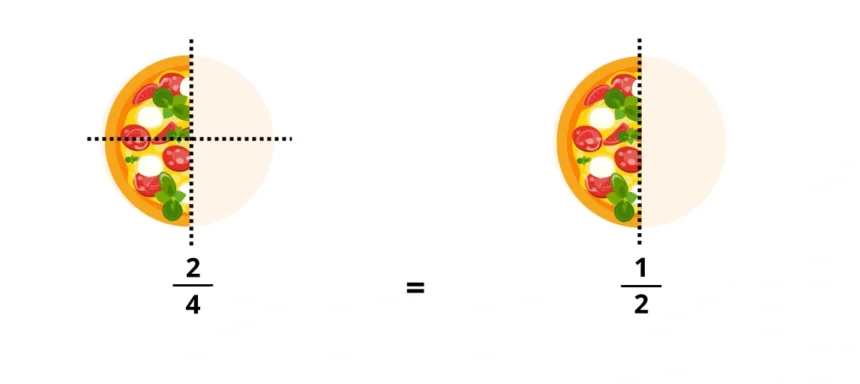
Wie beim Erweitern bleibt der vom Bruch dargestellte Wert unverändert. Kürzen ist das Gegenteil von Erweitern.

Beispiel: Du hast den Bruch und sollst ihn mit 2  kürzen.

Du teilst Zähler und Nenner durch 2. Im Zähler rechnest du 14:2 und im Nenner 36:2. Du erhältst den gekürzten Bruch.

= =

Manchmal ist es nicht möglich, den kleineren Nenner auf den größeren Nenner zu erweitern. Dann musst du beide Nenner auf ein gemeinsames Vielfaches erweitern. Wenn dir kein gemeinsames Vielfaches der beiden Nenner sofort ins Auge fällt, kannst du die Brüche auch einfach jeweils mit dem Nenner des anderen Bruchs erweitern.

Beispiel 2: Du hast die Brüche und und sollst diese addieren.

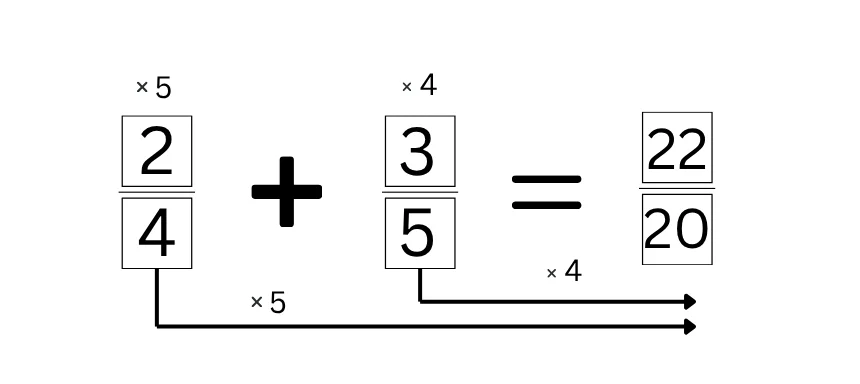
Brüche erweitern – Übungsaufgaben PDF zum sofort verstehen

Und jetzt bist du dran! Hier findest du Aufgaben, mit denen du üben kannst. Danach stehen dir die passenden Lösungen zu den Übungen zur Verfügung. Klicke einfach auf die Links und schon öffnen sich die Dateien.

Viel Erfolg beim Lernen!

[Aufgaben]

[Lösungen]