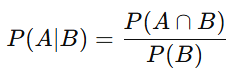(Noch keine Bewertungen)
Loading...
Die Stochastik beschäftigt sich mit Zufall, Wahrscheinlichkeit und Statistik. Sie hilft uns, Zufälle mathematisch zu beschreiben und besser zu verstehen, wie wahrscheinlich bestimmte Ereignisse eintreten. Ob in der Wirtschaft, Forschung oder im Alltag: Wer die Stochastik versteht, kann Risiken einschätzen und einfacher Entscheidungen treffen.
Lass und direkt loslegen!
Stochastik ist die mathematische Lehre vom Zufall. Sie befasst sich mit der Analyse und Berechnung von Wahrscheinlichkeiten sowie der Auswertung zufallsabhängiger Daten. Ziel ist es, unvorhersehbare Ereignisse mit Hilfe von Modellen verständlich und berechenbar zu machen.
Stochastik Grundlagen – das musst du wissen
Die Grundlagen der Stochastik sind entscheidend, um Zufälle und Wahrscheinlichkeiten richtig zu verstehen.
Wahrscheinlichkeitsrechnung
Die Wahrscheinlichkeitsrechnung zeigt, wie man berechnet, mit welcher Wahrscheinlichkeit ein Ereignis eintritt.
Absolute und relative Häufigkeit
Die absolute und relative Häufigkeit geben an, wie oft ein Ereignis tatsächlich vorkommt und welchen Anteil es am Gesamtergebnis hat.
Fakultät
Die Fakultät wird genutzt, um die Anzahl möglicher Anordnungen oder Kombinationen von Elementen zu bestimmen.
Binomialkoeffizient
Der Binomialkoeffizient hilft, Wahrscheinlichkeiten bei mehrfachen Versuchen oder Kombinationen zu berechnen.
Baumdiagramm
Das Baumdiagramm dient dazu, verschiedene Ereignisse und ihre Wahrscheinlichkeiten übersichtlich darzustellen.
Mengenlehre
Die Mengenlehre beschreibt, wie Ereignisse miteinander verknüpft sind. Zum Beispiel durch Schnittmengen oder Vereinigungen.
Wahrscheinlichkeitsrechnung
Die Wahrscheinlichkeitsrechnung bildet den ersten Kern der Stochastik. Sie beschäftigt sich damit, wie wahrscheinlich ein bestimmtes Ereignis eintritt. Dabei geht es darum, Zufälle messbar zu machen und Ergebnisse mathematisch zu bewerten.
Schauen wir uns die zwei wichtigsten Unterpunkte der Wahrscheinlichkeitsrechnung an!
Bedingte Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit beschreibt die Wahrscheinlichkeit eines Ereignisses unter der Bedingung, dass ein anderes Ereignis bereits eingetreten ist. Sie zeigt also, wie sich die Eintrittswahrscheinlichkeit verändert, wenn zusätzliche Informationen vorliegen. Bedingte Wahrscheinlichkeiten sind besonders wichtig, um Abhängigkeiten zwischen Ereignissen zu erkennen.
Die Formel zeigt, wie wahrscheinlich Ereignis A eintritt, unter der Bedingung, dass Ereignis B bereits eingetreten ist. Im Zähler steht die Wahrscheinlichkeit, dass beide Ereignisse gleichzeitig passieren und im Nenner die Wahrscheinlichkeit, dass B eintritt.
Kombinatorik
Die Kombinatorik beschäftigt sich damit, auf wie viele verschiedene Arten Ereignisse oder Objekte angeordnet oder kombiniert werden können. Sie hilft, die Anzahl möglicher Ergebnisse systematisch zu zählen, ohne alle Varianten einzeln auflisten zu müssen.
Typische Anwendungen sind Lottoziehungen, Sitzordnungen oder die Auswahl von Teams.
Mathematische Statistik
Die mathematische Statistik ist der zweite große Bereich der Stochastik. Sie beschäftigt sich damit, Daten zu sammeln, auszuwerten und daraus Schlüsse zu ziehen. Ziel ist es, Informationen über eine Grundgesamtheit aus Stichproben zu gewinnen. Mit ihren Methoden lassen sich Trends erkennen, Prognosen erstellen und Entscheidungen auf einer soliden Basis treffen.
Deskriptive Statistik
Die deskriptive Statistik fasst Daten zusammen und stellt sie übersichtlich dar. Sie dient dazu, große Datenmengen verständlich zu machen, ohne schon auf Schlussfolgerungen über die Grundgesamtheit zu gehen.
Wichtige Werkzeuge sind Tabellen, Diagramme, Mittelwerte, Median und Streuungsmaße. So lassen sich zentrale Tendenzen und Verteilungen schnell erkennen. Die deskriptive Statistik bildet damit die Grundlage für jede weitere statistische Analyse.
Induktive Statistik
Die induktive Statistik beschäftigt sich damit, von Stichprobendaten auf die gesamte Grundgesamtheit zu schließen. Sie nutzt Wahrscheinlichkeiten, um Aussagen über Trends oder Eigenschaften einer Population zu treffen.
Wichtige Methoden sind Schätzungen, Hypothesentests und Konfidenzintervalle. So können Entscheidungen getroffen werden, auch wenn nicht alle Daten bekannt sind. Die induktive Statistik ergänzt die deskriptive Statistik, indem sie Vorhersagen und Verallgemeinerungen ermöglicht.
Stochastik Aufgaben(stellungen) – das erwartet dich
Jetzt zeige ich dir, wie typische Aufgaben aus der Stochastik aussehen können, damit du ein Gefühl dafür bekommst, wie Wahrscheinlichkeiten, Kombinatorik und Statistik in der Praxis angewendet werden.
1: Berechne die Wahrscheinlichkeit, bei einem Würfel eine gerade Zahl zu werfen.
2: Bestimme die bedingte Wahrscheinlichkeit, dass es regnet, wenn die Wolken dunkel sind.
3: Wie viele Möglichkeiten gibt es, 3 Personen aus einer Gruppe von 10 auszuwählen?
4: Erstelle ein Baumdiagramm für zwei aufeinanderfolgende Münzwürfe.
5: Berechne den Mittelwert und die Standardabweichung der Noten einer Klasse.
6: Führe einen Hypothesentest durch, um zu prüfen, ob ein neues Medikament wirksam ist.
