Scheitelpunktform - in wenigen Minuten erklärt

4,67 von 5 Sterne

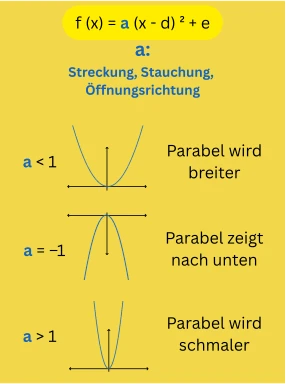
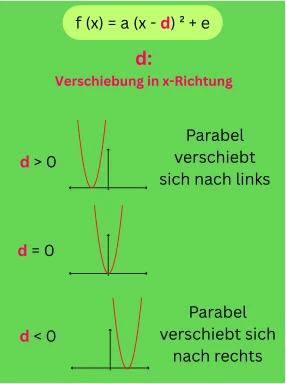
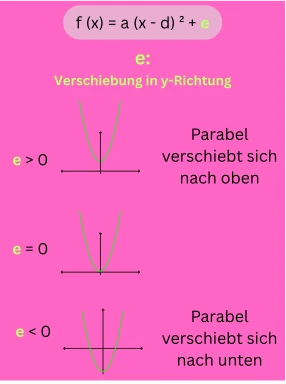
In diesem Artikel erkläre ich dir, was eine Scheitelpunktform einer quadratischen Funktion ist und wie du sie berechnen und den Scheitelpunkt ablesen kannst.

Außerdem lernst du, wie du Scheitelpunkte rechnerisch bestimmen kannst. Um dein Wissen zu vertiefen, stelle ich dir am Schluss noch ein paar Aufgaben mit Lösungen bereit.

Bereit? Na dann, los!

Inhalt

Scheitelpunktform – den Scheitelpunkt einer quadratischen Funktion erkennen!

Die Scheitelpunktform ist eine mathematische Form, um eine quadratische Funktion darzustellen.

Die allgemeine Scheitelpunktform lautet:

$f(x) = a(x-d)^2 + e$

$S(d|e)$

In dieser Form kann der Scheitelpunkt also sofort abgelesen werden.
Der Scheitelpunkt wird mit S abgekürzt. Wie bei einem gewöhnlichen Punkt ist die erste Zahl die x-Koordinate und die zweite die y-Koordinate.

Scheitelpunkt

Bei einer positiven quadratischen Funktion ist der Funktionsgraph nach oben geöffnet. Diese Parabel hat ihren Tiefpunkt als Scheitelpunkt. Die negative Funktion ist nach unten geöffnet und hat als Scheitelpunkt ihren höchsten Punkt.

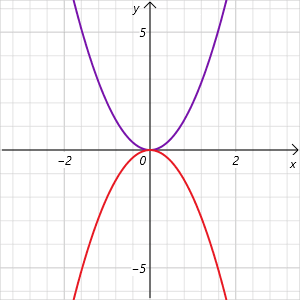
So bestimmst du den Scheitelpunkt einer Parabel:

Den Scheitelpunkt kannst du rechnerisch bestimmen. Ich zeige dir dazu 3 verschiedene Methoden, wie du den Scheitelpunkt bestimmen kannst.

1) Scheitelpunkt mit Hilfe der Scheitelpunktform ablesen
Wie oben erwähnt, kannst du den Scheitelpunkt direkt aus der Scheitelpunktform ablesen und bestimmen.

Was hier wichtig ist, ist das Vorzeichen in der Klammer!

Beispiel:

1. $f(x) = 3(x - 2)^2 + 2$

Hier kann man den Scheitelpunkt direkt ablesen, da die Funktion genau wie die Scheitelpunktform aussieht.

Der Scheitelpunkt liegt bei $S(2|2)$$ .

Beispiel:

2. $f(x) = 3(x + 2)^2 + 2$

Hier kann man den Scheitelpunkt ebenfalls ablesen, du musst allerdings auf das Vorzeichen in der Klammer achten, es muss ein Minuszeichen sein.

Dann heißt die Funktion:

$f(x) = 3(x - (-2))^2 + 2$

Der Scheitelpunkt liegt bei $S(-2|2)$ .

2) Scheitelpunkt mit Hilfe der allgemeinen Form (Quadratische Ergänzung) berechnen

Bei der quadratischen Ergänzung wird von der allgemeinen Form in die Scheitelpunktform umgewandelt. Es gibt vier einfache Schritte zu befolgen, um richtig umzuwandeln.

Dazu ein Beispiel:

Nehmen wir die Funktion

$f(x) = -\frac{1}{2}x^2 + x + 2$

1. Schritt: $f(x) = -\frac{1}{2}(x^2 - 2x) + 2$
2. Schritt: $f(x) = -\frac{1}{2}\left(x^2 - 2x + \left(\frac{2}{2}\right)^2 - \left(\frac{2}{2}\right)^2\right) + 2$
3. Schritt : $f(x) = -\frac{1}{2}(x^2 - 2x + 1 - 1) + 2$
4. Schritt: $f(x) = -\frac{1}{2}((x - 1)^2 - 1) + 2$
5. Schritt: $f(x) = -\frac{1}{2}(x - 1)^2 + \frac{1}{2} + 2$
6. Schritt: $f(x) = -\frac{1}{2}(x - 1)^2 + 2,5$

Der Scheitelpunkt liegt bei $S(1|2,5)$

3) Scheitelpunkt mit Hilfe der Ableitung berechnen

Wie ich dir schon oben erzählt habe, ist der Scheitelpunkt der Extrempunkt einer Funktion. Bei der Differenzialrechnung kannst du durchs Ableiten der Funktion ebenfalls den Scheitelpunkt berechnen.

Hier kannst du diese Schritte befolgen um den Scheitelpunkt zu erhalten:

Beispiel:

Nehmen wir die Funktion

$f(x) = 2x^2 + 4x + 3$

1. Schritt: $f'(x) = 4x + 4$

2. Schritt: $f'(x) = 0$

$x = -1$

$f'(x) = 0$

$0 = 4x + 4$ | -4

$-4 = 4x$ |: 4

3. Schritt:

$f(-1) = 2(-1)^2 + 4(-1) + 3$
$f(-1) = 2 - 4 + 3$
$S(-1|1)$

Somit liegt der Scheitelpunkt bei $S(-1|1)$

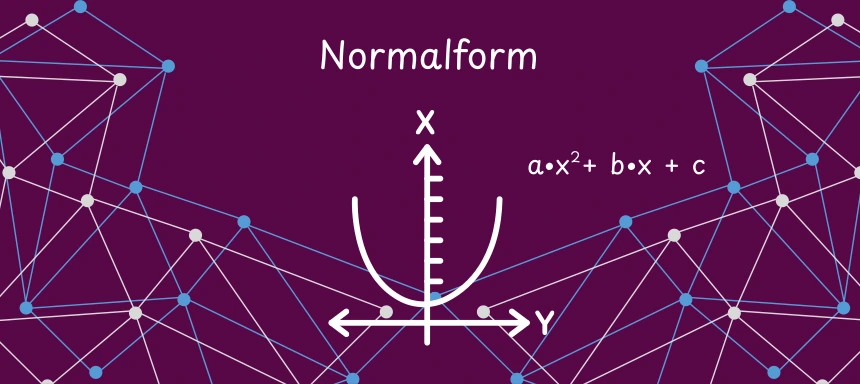
Scheitelpunktform in Normalform (allgemeine Form) umwandeln: Formel & Beispiel

Die allgemeine Form eignet sich, um den y-Achsenabschnitt sofort zu sehen, die Anzahl reeller Nullstellen zu beurteilen (per Diskriminante) und Standardverfahren wie pq-Formel oder Ableitung direkt anzuwenden.
Zur allgemeinen Form gelangt man aus der Scheitelpunktform, indem man die Klammer ausmultipliziert und gleichartige Terme zusammenfasst.

Wir wollen die Scheitelpunktform $f(x) = a(x - d)^2 + e$ mit dem Scheitelpunkt S $(d \mid e);(a \neq 0)$ in die Normalform $f(x) = ax^2 + bx + c;(a \neq 0)$    bringen, wobei: $b = -2ad, \qquad c = a d^2 + e$ ist.
Dabei helfen uns die binomischen Formeln:

$(a+b)^2 = a^2 + 2ab + b^2$
$(a-b)^2 = a^2 - 2ab + b^2$

Anhand zweier Beispiele formen wir die Scheitelpunktform in die allgemeine Form um:

Beispiel 1

Ausgangsform: $f(x)=-3(x-2)^2+7$
1. Klammer mithilfe der binomischen Formel ausklammern: $(x-2)^2=x^2-4x+4 ;\Rightarrow f(x)=-3(x^2-4x+4)+7$
2. Ausmultiplizieren: $f(x)=-3x^2+12x-12+7$
3. Zusammenfassen: $f(x)=\boxed{-3x^2+12x-5}$

Beispiel 2

Augsangsform: $f(x)=\frac{1}{2}(x+3)^2-4$
1. Klammer mithilfe der binomischen Formel ausklammern: $(x+3)^2=x^2+6x+9 ;\Rightarrow f(x)=\frac{1}{2}(x^2+6x+9)-4$
2. Ausmultiplizieren: $f(x)=\frac{1}{2}x^2+3x+4,5 - 4$
3. Zusammenfassen: $f(x)=\boxed{\frac{1}{2}x^2+3x +\frac{1}{2}}$

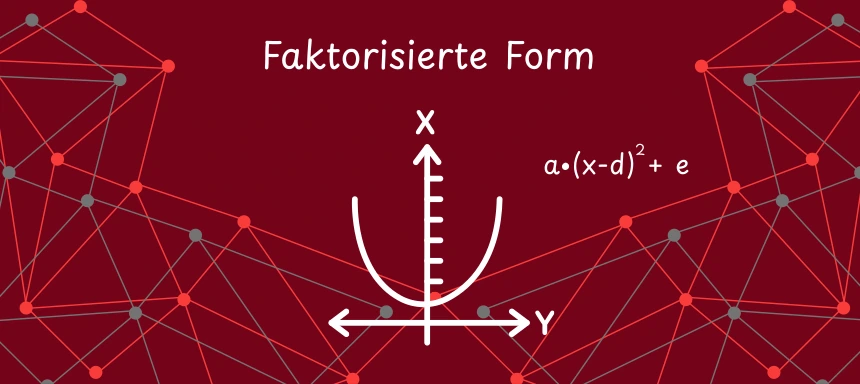
Scheitelpunktform in die faktorisierte Form (Nullstellenform) umwandeln: Formel & Beispiele

Die faktorisierte Form (auch: Nullstellenform) eignet sich, um die reellen Nullstellen einer Parabel direkt abzulesen.
Aus der Scheitelpunktform gelangt man dorthin, indem man die Funktion gleich null setzt, die Nullstellen bestimmt und die Funktion anschließend entsprechend schreibt.

Ausgangsform:  $f(x)=a(x-d)^2+e$

Schritt 1: Null setzen
Wir suchen die Nullstellen, also setzen wir $f(x)=0$ :
$0=a(x-d)^2+e$
Schritt 2: e subtrahieren
$-e=a(x-d)^2$
Schritt 3: Durch a teilen
$-\frac{e}{a}=(x-d)^2$
Schritt 4: Wurzel ziehen (immer mit ±!)
$x-d=\pm \sqrt{-\frac{e}{a}}$
Schritt 5: d auf die andere Seite bringen (d addieren)
$x=d\pm\sqrt{-\frac{e}{a}}$

Damit sind die (reellen) Nullstellen:
$x_1=d-\sqrt{-\frac{e}{a}}$ und $\qquad x_2=d+\sqrt{-\frac{e}{a}}$
Schritt 6: In die faktorisierte Form einsetzen
$f(x)=a(x-x_1)(x-x_2)$ bzw.   $f(x)=a\Bigl(x-\bigl(d-\sqrt{-\frac{e}{a}}\bigr)\Bigr)\Bigl(x-\bigl(d+\sqrt{-\frac{e}{a}}\bigr)\Bigr)$

Beispiel 1

Ausgangsform:  $f(x)=3(x-4)^2-2$

Schritt 1: Null setzen
Wir suchen die Nullstellen, also setzen wir $f(x)=0$ :
$0=3(x-4)^2-2$
Schritt 2: e subtrahieren
$2=3(x-4)^2$
Schritt 3: Durch a teilen
$\frac{2}{3}=(x-4)^2$
Schritt 4: Wurzel ziehen (immer mit ±!)
$x-4=\pm \sqrt{\frac{2}{3}}$
Schritt 5: d auf die andere Seite bringen (d addieren)
$x=4\pm\sqrt{\frac{2}{3}}$

Damit sind die (reellen) Nullstellen:
$x_1=4-\sqrt{\frac{2}{3}}$ und $\qquad x_2=4+\sqrt{\frac{2}{3}}$
Schritt 6: In die faktorisierte Form einsetzen
$f(x)=3(x-4-\sqrt{\frac{2}{3}})(x-4+\sqrt{\frac{2}{3}})$ bzw.   $f(x)=3\Bigl(x-\bigl(4-\sqrt{\frac{2}{3}}\bigr)\Bigr)\Bigl(x-\bigl(4+\sqrt{\frac{2}{3}}\bigr)\Bigr)$

Beispiel 2

Ausgangsform:  $f(x)=-2(x+2)^2+8$

Schritt 1: Null setzen
Wir suchen die Nullstellen, also setzen wir $f(x)=0$ :
$0=-2(x+2)^2+8$
Schritt 2: e subtrahieren
$-8=-2(x+2)^2$
Schritt 3: Durch a teilen
$\frac{8}{2}=(x+2)^2$
Schritt 4: Wurzel ziehen (immer mit ±!)
$x+2=\pm \sqrt{4}$
Schritt 5: d auf die andere Seite bringen (d addieren)
$x=-2\pm 2$

Damit sind die (reellen) Nullstellen:
$x_1=-4,$ und $x_2=0$
Schritt 6: In die faktorisierte Form einsetzen
$f(x)=-2(x-0)(x-(-4))=-2x(x+4)$

Soweit alles gut? Damit du dein Wissen nochmal überprüfen kannst, kannst du die folgenden Aufgaben bearbeiten und deine Ergebnisse mit dem Lösungsweg abgleichen. Viel Erfolg!