Mitternachtsformel einfach erklärt: in 5 Minuten verstehen

(Noch keine Bewertungen)

Du musst eine quadratische Gleichung lösen und weisst nicht genau, wie die Mitternachtsformel funktioniert? In diesem Artikel erklären wir dir einfach, wie du die Formel anwendest, mit Beispielen zum Nachrechnen und typischen Fehlern, die du vermeiden solltest.

Inhalt

Mitternachtsformel: Erklärung und Grundlagen

Mit der Mitternachtsformel, auch abc-Formel genannt, kann man quadratische Gleichungen mit der Form f(x) = ax² + bx + c lösen.

Man braucht die Mitternachtsformel, um Nullstellen der quadratischen Funktion zu bestimmen.

Wie lautet die Mitternachtsformel?

$x1,2=\frac{-b\pm\sqrt{b2-4ac}}{2a}$

Mit der Mitternachtsformel kann man die Ergebnisse x1 und x2 berechnen. Dafür setzt man die Werte für a, b und c ein und rechnet das Ergebnis einmal mit + und einmal mit – aus.

Der Teil unter der Wurzel, also $\sqrt{b^2 - 4ac}$ ist die Diskriminante (D) der Mitternachtsformel. Sie entscheidet, wie viele und welche Art von Lösungen es gibt.

D > 0 zwei verschiedene Lösungen
D = 0 eine Lösung
D < 0 keine reelle Lösung

Abgrenzung zu anderen Formeln – wo liegt der Unterschied?

Neben der Mitternachtsformel hast du bestimmt schonmal von der pq-Formel gehört.
Sie gilt für Gleichungen der Form x² + px + q = 0

Die pq Formel lautet:

$x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$

Die pq-Formel ist etwas einfacher als die Mitternachtsformel, sie funktioniert aber nur wenn der Faktor vor x² gleich 1 ist. Die abc-Formel funktioniert egal welche Zahl vor dem x² steht.

Bedingungen für die Anwendung der Mitternachtsformel

Damit du die Mitternachtsformel richtig anwenden kannst, muss es sich um eine quadratische Gleichung in der Form ax² + bx + c = 0 mit a ≠ 0 handeln

Die praktische Anwendung der Mitternachtsformel

Damit du die Mitternachtsformel besser verstehst, schauen wir uns ein Beispiel an:

x² + 6 = – 5x

Wir zeigen dir Schritt für Schritt, wie du die Mitternachtsformel anwendest.

1. Gleichung gleich 0 setzen

$x^2 + 6 = -5x \quad | +5x\\ x^2 + 5x + 6 = 0\\$

2. Koeffizienten a, b und c ablesen

$a = 1, \quad b = 5, \quad c = 6\\$

3. Koeffizienten in die Mitternachtsformel einsetzen

$x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\ x_{1,2} = \frac{-5 \pm \sqrt{5^2 - 4 \cdot 1 \cdot 6}}{2 \cdot 1}\\$

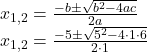
4. Ergebnisse ausrechnen

$x_{1,2} = \frac{-5 \pm \sqrt{25 - 24}}{2}\\ x_{1,2} = \frac{-5 \pm \sqrt{1}}{2}\\ x_{1,2} = \frac{-5 \pm 1}{2}x_1 = \frac{-5 + 1}{2} = \frac{-4}{2} = -2\\ \quad\quad x_2 = \frac{-5 - 1}{2} = \frac{-6}{2} = -3\\$

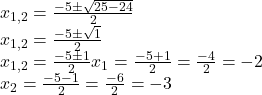
5. Nullstellen

$x_1 = -2, \quad x_2 = -3$

Typische Fehlerquellen

Beim Rechnen passieren oft kleine Fehler. Das ist normal und passiert jedem mal, ist aber vermeidbar. Hier sind ein paar Dinge, die du du beachten solltest, wenn du die Mitternachtsformel anwendest:

Vorsicht bei Vorzeichen beim Einsetzen in die Formel
Vorsicht beim Wurzelziehen!
Den Zähler beim Teilen in Klammern setzen → Den ganzen Zähler durch 2a teilen!

Übungsaufgaben zur Mitternachtsformel

Hast du alles zur Mitternachtsformel verstanden? Teste dein Wissen mit diesen Übungsaufgaben!

Aufgabe 1: Bestimme die Nullstellen der quadratischen Funktion

$\; 2x^2 + 6 = 8x$

mithilfe der Mitternachtsformel

$1. \; \textbf{Gleichung\ gleich\ 0\ setzen:}\\ 2x^2 + 6 = 8x \quad | -8x\\ 2x^2 + 6 - 8x = 0//2x^2 - 8x + 6 = 0\\ \\ 2. \; \textbf{Koeffizienten\ a\, b\ und\ c\ ablesen:}\\a = 2, \quad b = -8, \quad c = 6\\ \\ 3. \; \textbf{Koeffizienten\ in\ die\ Mitternachtsformel\ einsetzen:}\\ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\ x_{1,2} = \frac{8 \pm \sqrt{(-8)^2 - 4 \cdot 2 \cdot 6}}{2 \cdot 2} \]\\ \\ 4. \; \textbf{Ergebnisse\ ausrechnen:}\\x_{1,2} = \frac{8 \pm \sqrt{64 - 48}}{4}\\ x_{1,2} = \frac{8 \pm \sqrt{16}}{4}\\ x_{1,2} = \frac{8 \pm 4}{4} \\x_1 = \frac{8+4}{4} = 3\quad\quad\x_2 = \frac{8-4}{4} = 1\\ \\ 5. \; \textbf{Nullstellen:} x_1 = 3, \quad x_2 = 1 \]$

Aufgabe 2: Bestimme die Nullstellen der quadratischen Funktion mithilfe der Mitternachtsformel

$\;2x^2 - 5x = -3\\ 1. \; \textbf{Gleichung\ gleich\ 0\ setzen:}\\2x^2 - 5x = -3 \quad | +3\\ 2x^2 - 5x + 3 = 0\\ \\ 2. \; \textbf{Koeffizienten\ a\, b\ und\ c\ ablesen:}\\ a = 2, \quad b = -5, \quad c = 3\\ \\ 3. \; \textbf{Koeffizienten\ in\ die\ Mitternachtsformel\ einsetzen:} \\ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\ x_{1,2} = \frac{5 \pm \sqrt{(-5)^2 - 4 \cdot 2 \cdot 3}}{2 \cdot 2}\\ \\ 4. \; \textbf{Ergebnisse\ ausrechnen:}\\ x_{1,2} = \frac{5 \pm \sqrt{25 - 24}}{4}\\ x_{1,2} = \frac{5 \pm \sqrt{1}}{4}\\ x_{1,2} = \frac{5 \pm 1}{4}\\ x_1 = \frac{5+1}{4} = \frac{6}{4} = 1{,}5 \quad\quadx_2 = \frac{5-1}{4} = \frac{4}{4} = 1\\ \\ 5. \; \textbf{Nullstellen:}\\ x_1 = 1{,}5, \quad x_2 = 1$

FAQ zur Mitternachtsformel

Warum heißt die Mitternachtsformel so?

Die Mitternachtsformel heißt so, weil sie so wichtig ist, dass Schüler*innen sie selbst dann auswendig können sollten, wenn sie um Mitternacht geweckt werden, beziehungsweise sie im Schlaf aufsagen können sollten.

Wie lautet die pq-Formel?

$x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$

Was ist besser, die pq-Formel oder die Mitternachtsformel

Zwar kannst du mit beiden Formeln quadratische Gleichungen lösen, allerdings unterscheiden sie sich bei der Form der zu lösenden Gleichung. Mit der Mitternachtsformel löst du quadratische Gleichungen mit der Form f(x) = ax² + bx + c, mit der pq-Formel löst du Gleichungen der Form x² + px + q = 0. Es ist also nicht die Frage, welche der beiden Formeln besser ist, sondern welche quadratische Gleichung du lösen musst.

Wir haben viel Mühe in diesen Artikel gesteckt und freuen uns riesig, wenn du uns eine Sternebewertung hinterlässt. Vielen Dank!
(Noch keine Bewertungen)
Loading...

Mitternachtsformel einfach erklärt: in 5 Minuten verstehen