(Noch keine Bewertungen)
Loading...
Du hast gerade das Thema lineare Gleichungssysteme im Unterricht und weißt nicht, wie du Aufgaben dazu lösen kannst, was du machen sollst, wenn mehrere Unbekannte im Spiel sind, und wie du die graphisch darstellen sollst?
Dann bist Du hier genau richtig!
Fangen wir direkt an.
Eine lineare Gleichung besteht meistens aus ganzen Zahlen und beinhaltet eine Variable, also eine Unbekannte.
Da lineare Gleichungssysteme aus mindestens zwei linearen Gleichungen bestehen, beinhalten sie dementsprechend auch mindestens zwei Unbekannte.
Lineare Gleichungssysteme lösen
Lineare Gleichungssysteme lassen sich ganz allgemein mit Hilfe von Ausklammern und Äquivalenzumformungen lösen.
Es gibt jedoch drei verschiedene konkrete Möglichkeiten wie Du lineare Gleichungssysteme lösen kannst.
- Additionsverfahren
- Einsetzungsverfahren
- Gleichsetzungsverfahren
Additionsverfahren
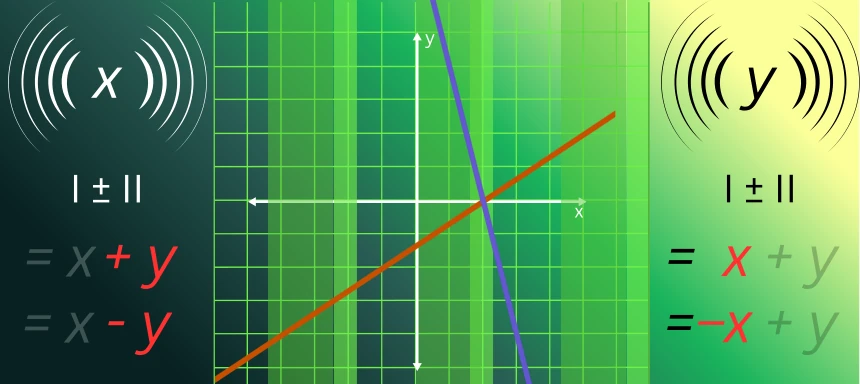
- Du solltest zuerst überlegen welche Variable du entfernen möchtest:
- Multipliziere dann die Gleichung so mit Zahlen, dass sich eine Unbekannte gegenseitig aufhebt.
- Danach müssen beide Gleichungen zusammen addiert werden, um eine neue Gleichung ohne die Unbekannte y zu erhalten.
- Zuletzt muss die Gleichung noch nach der anderen Variable, also in diesem Fall x aufgelöst werden.
- Anschließend kann man den Wert für x in eine der Variablen einsetzen, um den Wert für beide y-Variablen zu ermitteln.
Für ein näheres Verständnis, schaue Dir gerne unseren Artikel zum Additionsverfahren an 🙂
Einsetzungsverfahren
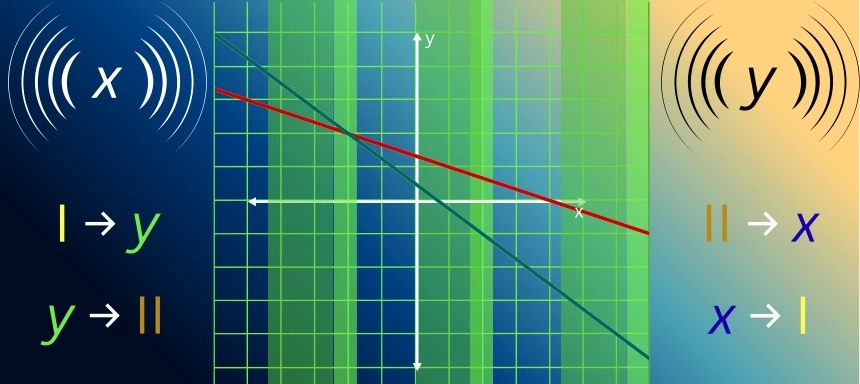
- Zuerst wählt man eine Gleichung aus, die man dann nach einer Variable umformt. Dabei spielt es keine Rolle, welche Gleichung und welche Variable.
- Nun setzt man die gerade umgeformte Variable in die andere Gleichung ein.
- Diese Gleichung formt man nun nach y um.
- Jetzt müssen wir einfach das gerade ermittelte y in die Gleichung a) einsetzen und damit die Variable x berechnen.
- So haben wir nun die Werte für beide Unbekannte.
Beachte beim umformen der Gleichungen immer die Punkt vor Strich Regel
Gleichsetzungsverfahren
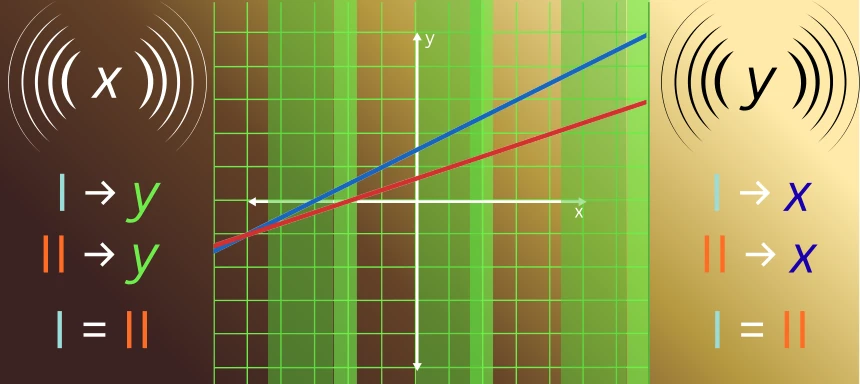
- Also zuerst werden beide Gleichungen nach einer Variable umgeformt.
- Die zwei Gleichungen für die Variable x werden nun im nächsten Schritt gleichgesetzt.
- Diese Gleichung muss jetzt im nächsten Schritt nach y aufgelöst.
- Um jetzt auch noch die andere Unbekannte (also in diesem Fall x) zu ermitteln, setzt man das errechnete y nun in eine der vorher gleichgesetzten Gleichungen ein.
Lineare Gleichungssysteme: Übungsaufgaben
Lineare Gleichungssysteme: Lösungen
Fällt Dir das Thema immer noch schwer? Dann schau Dir doch mal diese Playlist voller Videos zu linearen Gleichungssystemen an.
