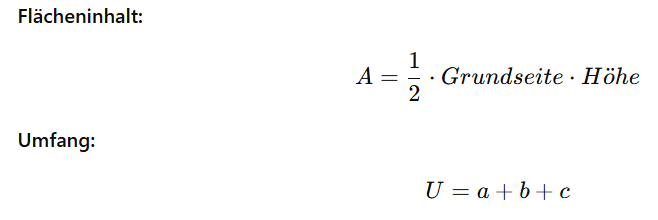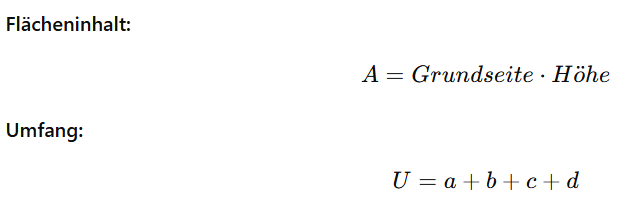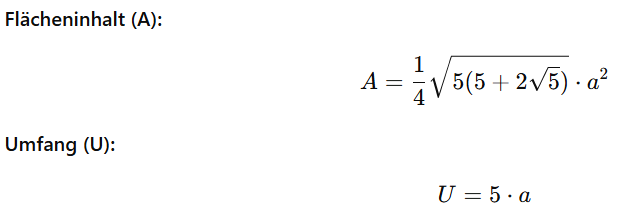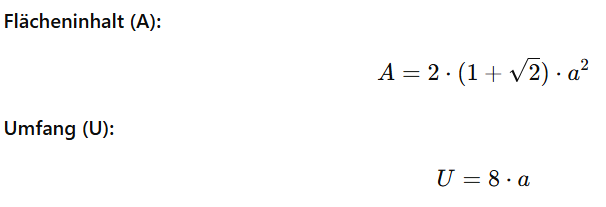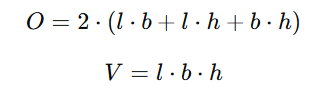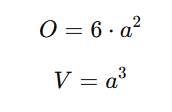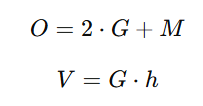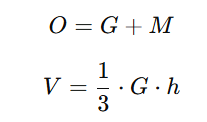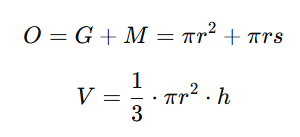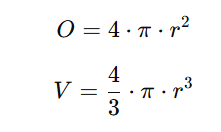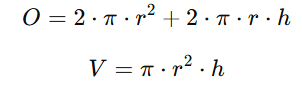(Noch keine Bewertungen)
Loading...
Geometrische Formen begegnen dir überall: in der Mathematik, im Alltag und sogar in der Natur. Sie bilden die Grundlage vieler Bereiche der Geometrie und helfen, Flächen, Körper und Zusammenhänge besser zu verstehen. Auf dieser Seite findest du eine Übersicht der wichtigsten geometrischen Formen. Von Kreis und Dreieck bis zu Würfel und Kugel. Und das ganze zusätzlich mit Erklärungen, Formeln und anschaulichen Beispielen.
Legen wir sofort los!
Geometrische Formen sind klar abgegrenzte Figuren, die durch Punkte, Linien, Flächen oder Körper in der Geometrie beschrieben werden. Sie dienen dazu, räumliche und flächenhafte Strukturen mathematisch darzustellen und zu untersuchen. Jede Form besitzt bestimmte Eigenschaften wie Seiten, Winkel, Kanten oder Flächen, die sie eindeutig beschreiben. In der Mathematik werden sie genutzt, um Größen, Abstände und Verhältnisse zu berechnen.
Grundsätzlich unterscheidet man zwischen zweidimensionalen (Flächenformen) und dreidimensionalen (Raumformen). Diese schauen wir uns in den nächsten Schritten genauer an.
Zweidimensionale geometrische Formen – 2D-Geometrie
Zweidimensionale geometrische Formen liegen in einer Ebene und besitzen nur Länge und Breite, aber keine Tiefe. Sie werden häufig genutzt, um Flächen oder Umfänge zu bestimmen. Zu dieser Kategorie zählen alle Formen, die du auf einer Fläche zeichnen kannst, von einfachen bis zu komplexeren Figuren.
Dreiecke
Dreiecke gehören zu den grundlegendsten zweidimensionalen Formen und unterscheiden sich vor allem durch ihre Seiten und Winkel. Es gibt:
- gleichschenklige Dreiecke, bei denen zwei Seiten gleich lang sind.
- gleichseitige Dreiecke, bei denen alle drei Seiten identisch sind.
- ungleichseitige Dreiecke haben alle Seiten unterschiedlich.
- spitzwinklige, rechtwinklige und stumpfwinklige Dreiecke werden anhand ihrer Winkel unterschieden.
Die Flächenformel nutzt die Grundseite und die Höhe, die senkrecht auf der Seite steht, während der Umfang einfach die Summe aller drei Seiten ist.
Vierecke
Vierecke sind Formen mit vier Seiten, die sehr vielseitig vorkommen. Es gibt:
- Rechtecke hat gegenüberliegende Seiten gleich lang und alle Winkel rechtwinklig.
- Quadrate haben alle Seiten gleich lang und alle Winkel rechtwinklig.
- Drachenvierecke haben zwei Paare benachbarter gleich langer Seiten und meist keine rechten Winkel.
Die Flächenformel berechnet die Fläche meist durch die Länge mal Breite oder durch spezielle Formeln beim Drachenviereck, während der Umfang die Summe aller vier Seiten ist.
Trapeze
Trapeze sind Vierecke mit genau zwei parallelen Seiten, die als Grundseiten bezeichnet werden. Es gibt:
- gleichschenklige Trapeze, bei denen die nicht-parallelen Seiten gleich lang sind.
- rechtwinklige Trapeze, die einen rechten Winkel besitzen.
- Außerdem lassen sich Trapeze in Parallelogramme und Raute einordnen, je nach Symmetrie und Seitenlängen.
Die Fläche wird über die Mittellinie zwischen den Grundseiten multipliziert mit der Höhe berechnet, während der Umfang die Summe aller vier Seiten ist.
Vielecke
Wichtig! Wir beziehen uns hierbei nur auf die regelmäßigen Formen!
Ein Pentagon hat 5 gleich lange Seiten. Bei regelmäßigen Vielecken sind alle Seiten und Winkel gleich. Der Flächeninhalt berücksichtigt die Geometrie des Fünfecks und die Seitenlänge Alpha. Der Umfang ist einfach die Summe aller Seiten.
Ein Hexagon hat 6 gleich lange Seiten. Ein regelmäßiges Hexagon lässt sich als 6 gleichseitige Dreiecke darstellen, daher der Faktor für den Flächeninhalt. Der Umfang ist die Summe aller Seiten.
Ein Oktagon hat 8 gleich lange Seiten. Der Flächeninhalt verwendet den Faktor, der aus der Aufteilung in Trapeze und Quadrate entsteht. Der Umfang ist die Summe aller Seiten.
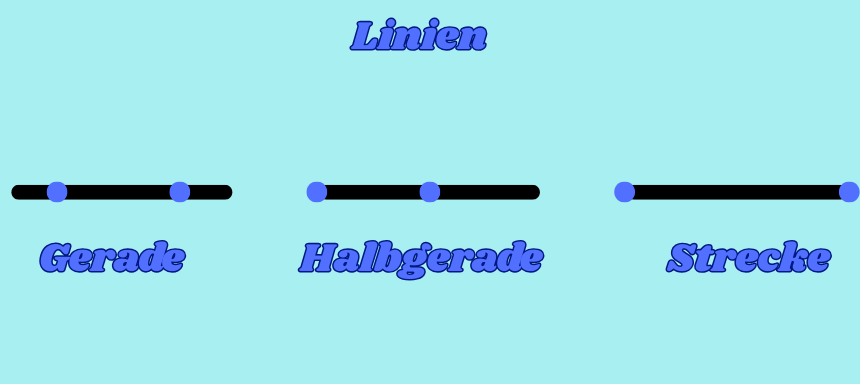
Punkt
Ein Punkt hat keine Ausdehnung, also weder Länge noch Fläche. Deshalb sind Flächeninhalt und Umfang immer 0. Er ist die grundlegendste geometrische Form und dient nur als Position oder Referenz im Raum.
Linie
Eine Gerade hat keinen Flächeninhalt und verläuft unendlich in beide Richtungen. Eine Halbgerade beginnt an einem Punkt und erstreckt sich unendlich in eine Richtung, ebenfalls ohne Flächeninhalt. Eine Strecke hat zwei Endpunkte, eine endliche Länge und ebenfalls keinen Flächeninhalt.
Kreis
Ein Kreis ist die Menge aller Punkte, die den gleichen Abstand r zum Mittelpunkt haben. Der Flächeninhalt wird mit pi x r² berechnet, wobei r der Radius ist. Der Umfang ist die Länge der Kreislinie und wird mit 2 x pi x r berechnet.
Dreidimensionale geometrische Formen – 3D-Geometrie
Dreidimensionale geometrische Formen besitzen neben Länge und Breite auch eine Höhe oder Tiefe und nehmen somit Raum ein. Sie werden in der 3D-Geometrie untersucht, wobei Volumen und Oberfläche zentrale Größen sind. Die verschiedenen Formen unterscheiden sich in ihrer Struktur und den geometrischen Eigenschaften.
Quader
Ein Quader ist ein rechteckiges Prisma mit sechs rechteckigen Flächen, bei dem Länge L, Breite B und Höhe H die Kanten bestimmen. Die Oberfläche O ergibt sich aus der Summe der Flächen aller sechs Seiten, während das Volumen V den Raum beschreibt, den der Quader einnimmt. Quader gehören zu den grundlegendsten 3D-Formen.
Würfel
Ein Würfel ist ein spezieller Quader, bei dem alle Kanten gleich lang sind (A). Die Oberfläche O besteht aus sechs gleich großen Quadraten, und das Volumen V beschreibt den gesamten Raum, den der Würfel einnimmt. Durch seine Symmetrie ist der Würfel eine der einfachsten und bekanntesten dreidimensionalen Formen.
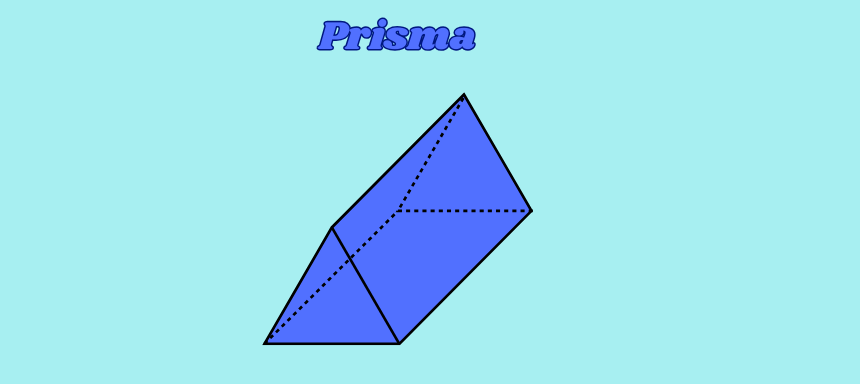
Prisma
Ein Prisma ist ein dreidimensionaler Körper mit zwei identischen, parallelen Grundflächen G und rechteckigen Seitenflächen, die die Grundflächen verbinden. Die Oberfläche O setzt sich aus der doppelten Grundfläche plus der Mantelfläche M zusammen, während das Volumen V durch die Grundfläche multipliziert mit der Höhe h berechnet wird. Prismen können verschiedene Grundflächen haben, z. B. Dreiecke, Vierecke oder andere Vielecke.
Pyramide
Eine Pyramide hat eine Grundfläche G und dreieckige Seitenflächen, die in einer Spitze zusammenlaufen. Die Oberfläche O setzt sich aus der Grundfläche und der Mantelfläche M zusammen, während das Volumen V ein Drittel der Grundfläche multipliziert mit der Höhe h beträgt. Pyramiden können unterschiedliche Grundformen haben, zum Beispiel dreieckig, viereckig oder polygonal.
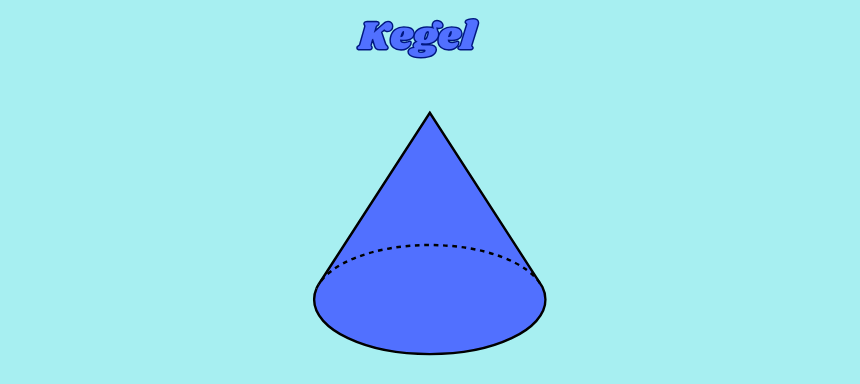
Kegel
Ein Kegel hat eine kreisförmige Grundfläche G mit Radius r und eine Mantelfläche M, die spitz zur Spitze des Kegels zusammenläuft. Die Oberfläche O setzt sich aus der Grundfläche plus der Mantelfläche zusammen, wobei s die Mantellinie ist. Das Volumen V entspricht einem Drittel der Grundfläche multipliziert mit der Höhe h.
Kugel
Eine Kugel ist eine vollkommen runde dreidimensionale Form, bei der alle Punkte auf der Oberfläche denselben Abstand r vom Mittelpunkt haben. Die Oberfläche O beschreibt die gesamte Außenfläche, während das Volumen V den Raum angibt, den die Kugel einnimmt. Aufgrund ihrer Symmetrie ist die Kugel eine der bekanntesten und am einfachsten zu berechnenden 3D-Formen.
Zylinder
Ein Zylinder hat zwei kreisförmige Grundflächen mit Radius r und eine rechteckige Mantelfläche, die sich um die Grundflächen legt. Die Oberfläche O setzt sich aus den beiden Grundflächen plus der Mantelfläche zusammen, während das Volumen V durch die Grundfläche multipliziert mit der Höhe h berechnet wird.
